快速排序
快速排序类似于归并,也有分治的一种思想,即找到一个基准数,将比它大的放在它的右边,比它小的放在它的左边。(这真的没啥好说的,直接看代码)
#include<iostream>
using namespace std;
int n,a[1000001];
void qsort(int l,int r)//应用二分思想
{
int mid=a[(l+r)/2];// 取中间数为基准数
int i=l,j=r;
do{
while(a[i]<mid) i++;// 查找左半部分比中间数大的数
while(a[j]>mid) j--;// 查找右半部分比中间数小的数
if(i<=j)// 如果有一组不满足排序条件(左小右大)的数
{
swap(a[i],a[j]);// 交换
i++;
j--;
}
}while(i<=j);// 这里注意要有=
if(l<j) qsort(l,j);// 递归搜索左半部分
if(i<r) qsort(i,r);// 递归搜索右半部分
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
qsort(1,n);
for(int i=1;i<=n;i++) cout<<a[i]<<" ";
}
折半查找
折半查找,也称二分查找,在某些情况下相比于顺序查找,使用折半查找算法的效率更高。但是该算法的使用的前提是静态查找表中的数据必须是有序的。
例题:对静态查找表`{-32, 12, 16, 24, 36, 45, 59, 98}`采用折半查找算法查找关键字为12 的元素。
图解

样例代码
#include <stdio.h>
binarySearch(int a[], int n, int key){
int low = 0;
int high = n - 1;
while(low<= high){
int mid = (low + high)/2;
int midVal = a[mid];
if(midVal<key)
low = mid + 1;
else if(midVal>key)
high = mid - 1;
else
return mid;
}
return -1;
}
int main(){
int i, val, ret;
int a[8]={-32, 12, 16, 24, 36, 45, 59, 98};
for(i=0; i<8; i++)
printf("%d ", a[i]);
printf("
请输人所要查找的元素:");
scanf("%d",&val);
ret = binarySearch(a,8,val);
if(-1 == ret)
printf("查找失败
");
else
printf ("查找成功
");
return 0;
}
冒泡排序
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。
作为最简单的排序算法之一,冒泡排序给我的感觉就像 Abandon 在单词书里出现的感觉一样,每次都在第一页第一位,所以最熟悉。冒泡排序还有一种优化算法,就是立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。但这种改进对于提升性能来
说并没有什么太大作用。
动画了解冒泡排序原理

样例代码
#include <stdio.h>
void bubble_sort(int arr[], int len) {
int i, j, temp;
// 外层循环和内层循环分别取出
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
// 如果第一个比第二个大,就交换他们两个。
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
int main() {
int arr[14] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = 14; // len代表数组的长度
bubble_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
return 0;
}
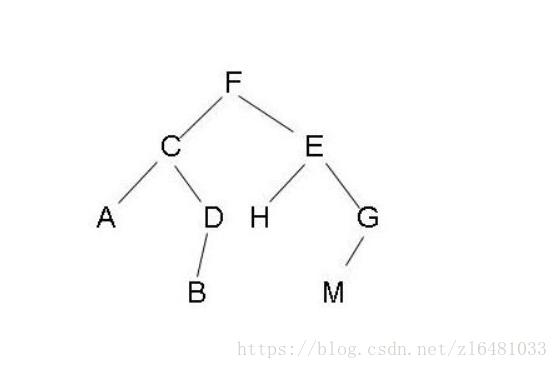
树前中后序遍历
三种遍历的概念
(1)先序遍历:先访问根节点,再访问左子树,最后访问右子树。
(2) 后序遍历:先左子树,再右子树,最后根节点。
(3)中序遍历:先左子树,再根节点,最后右子树。
如下图
先序遍历:FCADBEHGM
后序遍历:ABDCHMGEF
中序遍历:ACBDFHEMG
因为树的相关题目众多且形式都不一样老方估计也不会出复杂的题目,在此仅仅贴出三种遍历的最简单实现,省去构建树的过程
//遍历实现先序
//根左右
void PreOrder(Tree T)
{
if(T)
{
printf("%d",T->Element);//输出根节点,可以是其他操作
PreOrder(T->Left);
PreOrder(T->Right);
}
}
//遍历实现中序
//左根右
void PreOrder(Tree T)
{
if(T)
{
PreOrder(T->Left);
printf("%d",T->Element);//输出根节点,可以是其他操作
PreOrder(T->Right);
}
}
//遍历实现后序
//左右根
void PreOrder(Tree T)
{
if(T)
{
PreOrder(T->Left);
PreOrder(T->Right);
printf("%d",T->Element);//输出根节点,可以是其他操作
}
}
深度,广度优先搜索
这章不太好讲,建议直接了解概念即可
深度优先搜索和广度优先搜索,都是图形搜索算法,它两相似,又却不同,在应用上也被用到不同的地方。这里拿一起讨论,方便比较。
一、深度优先搜索
深度优先搜索属于图算法的一种,是一个针对图和树的遍历算法,英文缩写为DFS即Depth First Search。深度优先搜索是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
基本步奏
(1)对于下面的树而言,DFS方法首先从根节点1开始,其搜索节点顺序是1,2,3,4,5,6,7,8(假定左分枝和右分枝中优先选择左分枝)。

(2)从stack中访问栈顶的点;

(3)找出与此点邻接的且尚未遍历的点,进行标记,然后放入stack中,依次进行;

(4)如果此点没有尚未遍历的邻接点,则将此点从stack中弹出,再按照(3)依次进行;


(5)直到遍历完整个树,stack里的元素都将弹出,最后栈为空,DFS遍历完成。


二、广度优先搜索
广度优先搜索(也称宽度优先搜索,缩写BFS,以下采用广度来描述)是连通图的一种遍历算法这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。基本过程,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止。一般用队列数据结构来辅助实现BFS算法。
基本步奏
(1)给出一连通图,如图,初始化全是白色(未访问);

(2)搜索起点V1(灰色);

(3)已搜索V1(黑色),即将搜索V2,V3,V4(标灰);

(4)对V2,V3,V4重复以上操作;

(5)直到终点V7被染灰,终止;

(6)最短路径为V1,V4,V7.
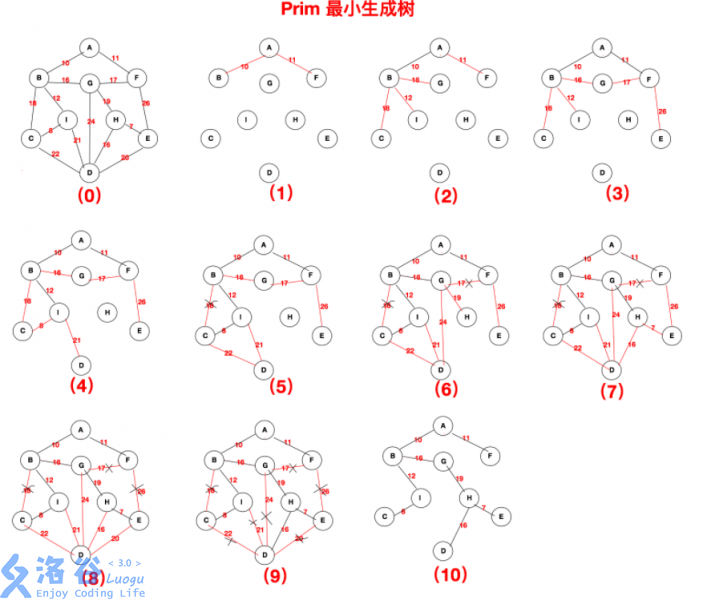
prim和kruscal算法
prim算法:
个人觉得Prim和最短路中的dijkstra很像,由于速度问题,所以这里我用链式前向星存图。Prim的思想是将任意节点作为根,再找出与之相邻的所有边(用一遍循环即可),再将新节点更新并以此节点作为根继续搜,维护一个数组:dis,作用为已用点到未用点的最短距离。
证明:Prim算法之所以是正确的,主要基于一个判断:对于任意一个顶点v,连接到该顶点的所有边中的一条最短边(v, vj)必然属于最小生成树(即任意一个属于最小生成树的连通子图,从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树)
一图了解prim算法
样例代码(在此仅贴出核心代码块)
int prim()
{
//先把dis数组附为极大值
for(re int i=2;i<=n;++i)
{
dis[i]=inf;
}
//这里要注意重边,所以要用到min
for(re int i=head[1];i;i=e[i].next)
{
dis[e[i].v]=min(dis[e[i].v],e[i].w);
}
while(++tot<n)//最小生成树边数等于点数-1
{
re int minn=inf;//把minn置为极大值
vis[now]=1;//标记点已经走过
//枚举每一个没有使用的点
//找出最小值作为新边
//注意这里不是枚举now点的所有连边,而是1~n
for(re int i=1;i<=n;++i)
{
if(!vis[i]&&minn>dis[i])
{
minn=dis[i];
now=i;
}
}
ans+=minn;
//枚举now的所有连边,更新dis数组
for(re int i=head[now];i;i=e[i].next)
{
re int v=e[i].v;
if(dis[v]>e[i].w&&!vis[v])
{
dis[v]=e[i].w;
}
}
}
return ans;
}
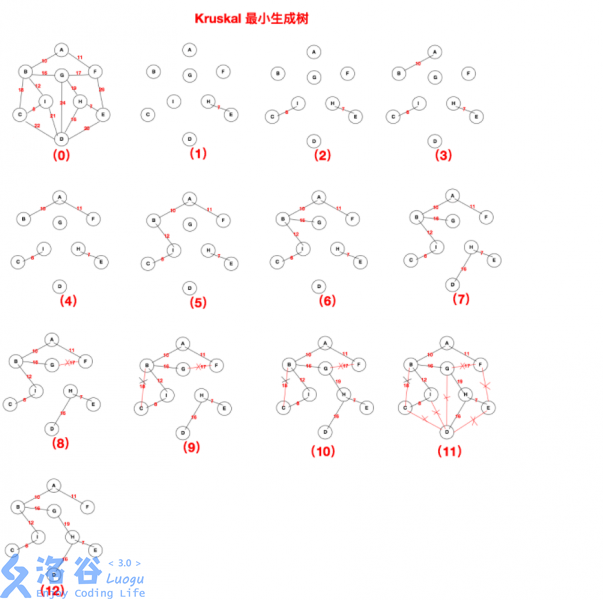
Kruskal算法:
Kruskal算法的思想比Prin好理解一些。先把边按照权值进行排序,用贪心的思想优先选取权值较小的边,并依次连接,若出现环则跳过此边(用并查集来判断是否存在环)继续搜,直到已经使用的边的数量比总点数少一即可。
证明:刚刚有提到:如果某个连通图属于最小生成树,那么所有从外部连接到该连通图的边中的一条最短的边必然属于最小生成树。所以不难发现,当最小生成树被拆分成彼此独立的若干个连通分量的时候,所有能够连接任意两个连通分量的边中的一条最短边必然属于最小生成树
一图了解Kruskal算法:
样例代码(在此仅贴出核心代码块)
//并查集循环实现模板,及路径压缩,不懂并查集的同学可以戳一戳代码上方的“并查集详解”
il void kruskal()
{
sort(edge,edge+m,cmp);
//将边的权值排序
for(re int i=0;i<m;i++)
{
eu=find(edge[i].u), ev=find(edge[i].v);
if(eu==ev)
{
continue;
}
//若出现两个点已经联通了,则说明这一条边不需要了
ans+=edge[i].w;
//将此边权计入答案
fa[ev]=eu;
//将eu、ev合并
if(++cnt==n-1)
{
break;
}
//循环结束条件,及边数为点数减一时
}
}
01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
算法1:
二维数组+动态规划
动态规划知识先导
状态转换方程:
定义f[i][j]:前i个物品,背包容量j下的最优解
(1) 当前背包容量不够(j<w[i]),为前i-1个物品最优解:
f[i][j]=f[i-1][j]
(2) 当前背包容量够,判断选与不选第i个物品
选:f[i][j] = f[i-1][j-w[i]] + v[i]
不选:f[i][j] = f[i-1][j]
参考代码:
#include<bits/stdc++.h>
using namespace std;
int N,V;
int v[1020],w[1020];
int dp[1020][1020];
int main()
{
cin>>N>>V;
for(int i=1;i<=N;i++)
cin>>v[i]>>w[i];
for(int i=1;i<=N;i++)
{
for(int j=V;j>=0;j--)
{
if(j>=v[i])
dp[i][j]=max(dp[i-1][j-v[i]]+w[i],dp[i-1][j]);
else
dp[i][j]=dp[i-1][j];
}
}
cout<<dp[N][V];
return 0;
}
二叉树的前中后序遍历
前面已经讲过树的前中后序遍历了,这里只贴代码
class Solution {
public:
void inorder(TreeNode* root, vector<int>& res) {
if (!root) {
return;
}
// 二叉树的前中后序遍历的不同体现在这个部分
// 这是二叉树的前序遍历(根左右)
res.push_back(root->val);
inorder(root->left, res);
inorder(root->right, res)
// 这是二叉树的中序遍历(左根右)
inorder(root->left, res);
res.push_back(root->val);
inorder(root->right, res);
// 这是二叉树的后序遍历(左右根)
inorder(root->left, res);
inorder(root->right, res);
res.push_back(root->val);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
inorder(root, res);
return res;
}
};
树的广度优先遍历

1.广度优先遍历
英文缩写为BFS即Breadth FirstSearch。其过程检验来说是对每一层节点依次访问,访问完一层进入下一层,而且每个节点只能访问一次。对于上面的例子来说,广度优先遍历的 结果是:A,B,C,D,E,F,G,H,I(假设每层节点从左到右访问)。
先往队列中插入左节点,再插右节点,这样出队就是先左节点后右节点了。
广度优先遍历树,需要用到队列(Queue)来存储节点对象,队列的特点就是先进先出。例如,上面这颗树的访问如下:
首先将A节点插入队列中,队列中有元素(A);
将A节点弹出,同时将A节点的左、右节点依次插入队列,B在队首,C在队尾,(B,C),此时得到A节点;
继续弹出队首元素,即弹出B,并将B的左、右节点插入队列,C在队首,E在队尾(C,D,E),此时得到B节点;
继续弹出,即弹出C,并将C节点的左、中、右节点依次插入队列,(D,E,F,G,H),此时得到C节点;
将D弹出,此时D没有子节点,队列中元素为(E,F,G,H),得到D节点;
。。。以此类推。。
代码:这里以二叉树为例,遍历所有节点的值
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> lists=new ArrayList<Integer>();
if(root==null)
return lists;
Queue<TreeNode> queue=new LinkedList<TreeNode>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode tree=queue.poll();
if(tree.left!=null)
queue.offer(tree.left);
if(tree.right!=null)
queue.offer(tree.right);
lists.add(tree.val);
}
return lists;
}
}