【模板】后缀排序（SA数组）

【模板】后缀排序

题目背景

这是一道模板题。

题目描述

读入一个长度为 (n) 的由大小写英文字母或数字组成的字符串，请把这个字符串的所有非空后缀按字典序从小到大排序，然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 (1) 到 (n) 。

输入输出格式

输入格式：

一行一个长度为 (n) 的仅包含大小写英文字母或数字的字符串。

输出格式：

一行，共 (n) 个整数，表示答案。

输入输出样例

输入样例#1： 复制

ababa

输出样例#1： 复制

5 3 1 4 2

说明

(n <= 10^6)

---

一点点理解？

怎么说呢？
后缀数组是用来处理字符串后缀的有效手段。
虽然 DC3 的时间复杂度比 倍增 要少了一个log。
但是我们在平常中还是用倍增更多一些。
倍增是用基数排序来维护的。
事先说明。我学的后缀数组资源来源与自为风月马前卒大佬的博客（强烈推荐）。
rak[i]=表示后缀开头位置为 i 的排名,也是第一关键词
num[i]=桶计数
tp[i]=第二关键词，也就是基数排序的后半段
sa[i]=第i个排名的后缀的开头位置


先来看个图



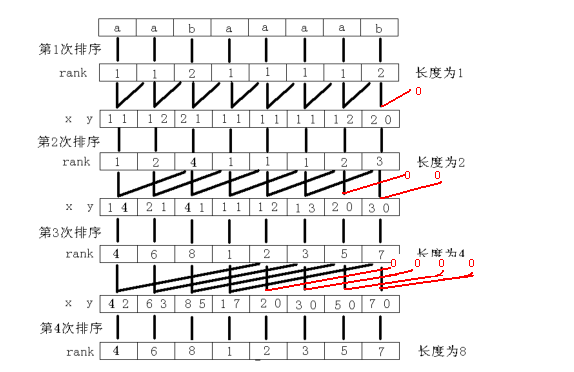
接下来看代码

void Sort()
{ 
	for(int i=0;i<=m;i++)num[i]=0; 
	for(int i=1;i<=n;i++)num[rak[i]]++; 
	for(int i=1;i<=m;i++)num[i]+=num[i-1]; 
	for(int i=n;i>=1;i--)sa[num[rak[tp[i]]]--]=tp[i]; 
}

这时候比较难理解的就是最后一句对吧,别急,看后面的代码。

	cnt=0;
	for(int i=1;i<=w;i++)tp[++cnt]=n-w+i; 
	for(int i=1;i<=n;i++)if(sa[i]>w)tp[++cnt]=sa[i]-w;

这是第一次倍增时的确定tp[]值的代码。
为什么先把后面的tp[]值赋为后面小于ｗ(w为当前排序的长度)呢？
因为后面的长度小于等于ｗ的字符串，再怎么倍增第二关键词都是空集，就相当于只比第一关键词。
第二句话，如果sa[i]的位置能在倍增时作为前面第一关键词的第二关键词，那么便让当前第二关键词的位置等于第一关键词。
因为这里sa[i]已经排序好了，所以其实我们是已经求好了第二关键词的大小的，这样就只要回到第一关键词的大小比较即可。
此时sa[num[rak[tp[i]]--]=tp[i]　事实上就是在排好了第二关键词的情况下，求出来的第一关键词的sa[]值。不过这一次的sa[]值已经是第一关键词和第二关键词的总和的字符串的位置。

---

代码

	#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1000100;
char s[N];
int sa[N],rak[N],tp[N],num[N];
int n,m=200;
void Sort(){
    for(int i=0;i<=m;i++)num[i]=0;
    for(int i=1;i<=n;i++)num[rak[i]]++;
    for(int i=1;i<=m;i++)num[i]+=num[i-1];
    for(int i=n;i>=1;i--)sa[num[rak[tp[i]]]--]=tp[i];
}

void SA_sort(){
    for(int i=1;i<=n;i++){
        rak[i]=s[i]-'0',tp[i]=i;
    }
    Sort();
    int p=0,w=1,cnt;
    while(p<n){
        cnt=0;
        for(int i=1;i<=w;i++)tp[++cnt]=n-w+i;
        for(int i=1;i<=n;i++)if(sa[i]>w)tp[++cnt]=sa[i]-w;
        Sort();swap(rak,tp);
        rak[sa[1]]=p=1;
        for(int i=2;i<=n;i++)
        if((tp[sa[i]]==tp[sa[i-1]])&&(tp[sa[i]+w]==tp[sa[i-1]+w]))
        rak[sa[i]]=p;
        else rak[sa[i]]=++p;
        w<<=1;m=p;
    }
}

int main(){
    scanf("%s",s+1);
    n=strlen(s+1);
    SA_sort();
    for(int i=1;i<=n;i++)
    {
        printf("%d ",sa[i]);
    }
    return 0;
}