两个变量之间的交换,通过查阅资料,有如下四种常见方法:
1.利用一个中间变量实现交换
int a, b;
int temp;
temp = a;
a = b;
b = temp;
2.利用+-操作实现
int a, b; //a = 1 b = 2
a = a + b; //a = 3 b = 2
b = a - b; //b = 1 a = 3
a = a - b; //a = 2 b = 1
3.利用乘除操作实现
int a, b;
a = a * b;
b = a / b;
a = a / b;
4.利用异或操作实现(当a,b相等时,不可用)
int a, b;
a = a ^ b;
b = a ^ b;
a = a ^ b;
数组的冒泡排序法:
冒泡排序是最简单的排序方法,理解起来容易。虽然它的计算步骤比较多,不是最快的,但它是最基本的,初学者一定要掌握。
冒泡排序的原理是:从左到右,相邻元素进行比较。每次比较一轮,就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。
以从小到大排序为例,第一轮比较后,所有数中最大的那个数就会浮到最右边;第二轮比较后,所有数中第二大的那个数就会浮到倒数第二个位置……就这样一轮一轮地比较,最后实现从小到大排序。
比如对下面这个序列进行从小到大排序:90 21 132 -58 34
第一轮:
1) 90 和 21比,90>21,则它们互换位置:21 90 132 -58 34
2) 90 和 132 比,90<132,则不用交换位置。
3)132 和 –58 比,132>–58,则它们互换位置:21 90 -58 132 34
4)132 和 34 比,132>34,则它们互换位置:
21 90 -58 34 132
到此第一轮就比较完了。第一轮的结果是找到了序列中最大的那个数,并浮到了最右边。
比较时,每轮中第 n 次比较是新序列中第 n 个元素和第 n+1 个元素的比较(假如 n 从 1 开始)。
第二轮:
1) 21 和 90 比,21<90,则不用交换位置。
2) 90 和 –58 比,90>–58,则它们互换位置:21 -58 90 34 132
3) 90 和 34 比,90>34,则它们互换位置:
21 -58 34 90 132
到此第二轮就比较完了。第二轮的结果是找到了序列中第二大的那个数,并浮到了最右边第二个位置。
第三轮:
1) 21 和 –58 比,21>–58,则它们互换位置:-58 21 34 90 132
2) 21 和 34 比,21<34,则不用交换位置。到此第三轮就比较完了。第三轮的结果是找到了序列中第三大的那个数,并浮到了最右边第三个位置。第四轮:1) –58 和 21 比,–58<21,则不用交换位置。至此,整个序列排序完毕。从小到大的序列就是“–58 21 34 90 132”。从这个例子中还可以总结出,如果有 n 个数据,那么只需要比较 n–1 轮。而且除了第一轮之外,每轮都不用全部比较。因为经过前面轮次的比较,已经比较过的轮次已经找到该轮次中最大的数并浮到右边了,所以右边的数不用比较也知道是大的
拓展:
通过在vs上调试:运用了引用第三变量和异或法分别调试
引入第三变量法:
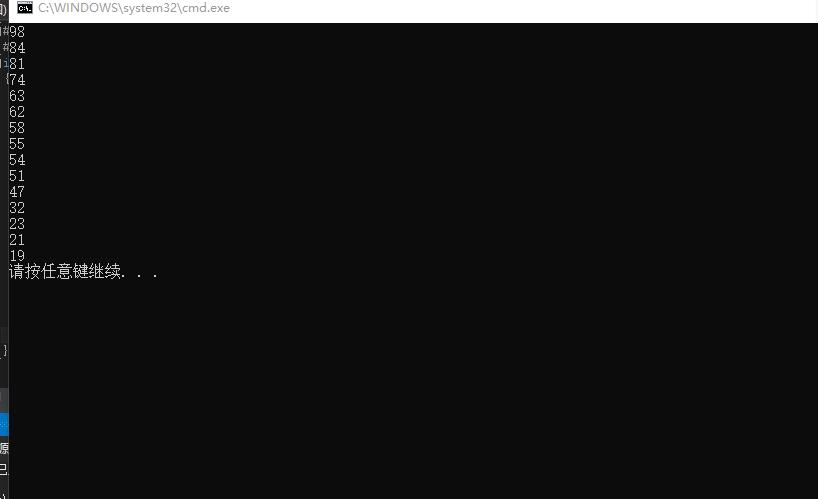
1 #include <stdio.h> 2 #include <stdlib.h> 3 int main() 4 { 5 int i, j, tem; 6 int arr1[] = { 81, 51, 62, 84, 74, 21, 32, 16, 58, 63, 19, 54, 23, 98, 47, 55 }; 7 for (i = 0; i< 15; i++){ 8 for (j = 0; j < 15 - i; j++){ 9 if (arr1[j] < arr1[j + 1]){ 10 tem = arr1[j]; 11 arr1[j] = arr1[j + 1]; 12 arr1[j + 1] = tem; 13 } 14 } 15 } 16 for (i = 0; i < 15; i++){ 17 printf("%d ", arr1[i]); 18 } 19 system("pause"); 20 return 0; 21 }
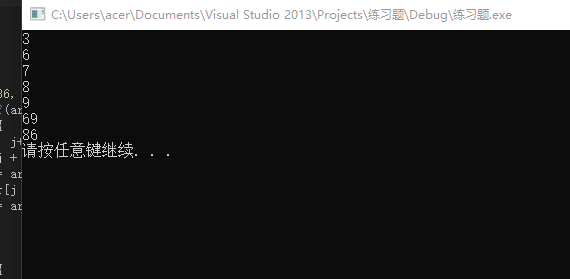
1 冒泡排序法 2 #include <stdio.h> 3 #include <stdlib.h> 4 int main() 5 { 6 int i, j, k; 7 int arr[] = { 8, 6, 7, 86, 9, 3, 69 }; 8 k = sizeof(arr) / sizeof(arr[0]); 9 for (i = 1; i <k ; i++){ 10 for (j = 0; j < k-i; j++){ 11 if (arr[j]>arr[j + 1]){ 12 arr[j + 1] = arr[j+1]^arr[j]; 13 arr[j] = arr[j + 1]^arr[j]; 14 arr[j + 1] = arr[j + 1] ^ arr[j]; 15 } 16 } 17 } 18 for (i = 0; i < k; i++){ 19 printf("%d ", arr[i]); 20 } 21 system("pause"); 22 return 0; 23 }
程序中,为什么每轮比较的次数是 j<k-i,而不是 j<k–1?
因为冒泡排序有一个特点,这个程序是从大到小排序,所以第一轮排序以后,
最小的数就会浮到最右面;第二轮排序以后,第二小的数会浮到倒数第二个位置;
第三轮排序以后,第三小的数会浮到倒数第三个位置……也就是说,排序多少轮,
就有多少个数字已经按排序要求排好了,它们不需要再比较。写 j<k–1 也可以,
只不过程序在执行时多做了许多无用功
1 #include <stdio.h> 2 int main() 3 { 4 int arr1[] = { 1, 3, 5, 7, 9 }; 5 int arr2[] = { 3, 4, 5, 6, 7 }; 6 int tmp; 7 int i = 0; 8 for (i = 0; i < sizeof(arr1) / sizeof(arr1[0]); i++) 9 { 10 tmp = arr1[i]; 11 arr1[i] = arr2[i]; 12 arr2[i] = tmp; 13 } 14 for (i = 0; i < sizeof(arr1) / sizeof(arr1[0]); i++) 15 { 16 printf("%d ", arr1[i]); 17 } 18 printf(" "); 19 for (i = 0; i < sizeof(arr1) / sizeof(arr1[0]); i++) 20 { 21 printf("%d ", arr2[i]); 22 } 23 printf(" "); 24 return 0; 25 }
加减法:
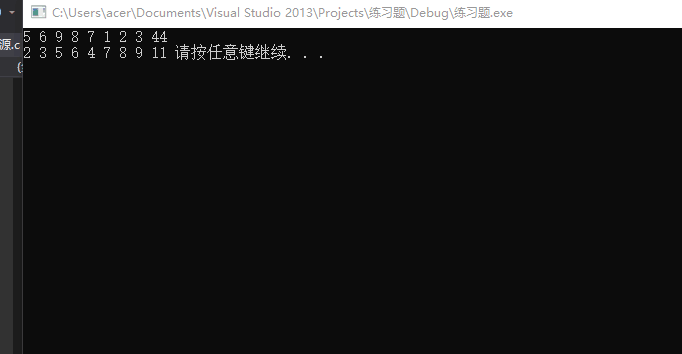
1 #include <stdio.h> 2 #include <stdlib.h> 3 int main() 4 { 5 int arr1[] = { 2, 3, 5, 6, 4, 7, 8, 9, 11 }; 6 int arr2[]= {5, 6, 9, 8, 7, 1, 2, 3, 44}; 7 int i; 8 for (i = 0; i < 9; i++){ 9 arr1[i] = arr1[i] + arr2[i]; 10 arr2[i] = arr1[i] - arr2[i]; 11 arr1[i] = arr1[i] - arr2[i]; 12 } 13 for (i = 0; i < 9; i++){ 14 printf("%d ", arr1[i]); 15 } 16 printf(" "); 17 for (i = 0; i < 9; i++){ 18 printf("%d ", arr2[i]); 19 } 20 21 system("pause"); 22 return 0; 23 }
异或法:
1 用异或法互换 2 #include <stdio.h> 3 #include <stdlib.h> 4 int main() 5 { 6 int arr1[] = { 2, 3, 5, 6, 4, 7, 8, 9, 11 }; 7 int arr2[] = { 5, 6, 9, 8, 7, 1, 2, 3, 44 }; 8 int i; 9 for (i = 0; i < 9; i++){ 10 arr1[i] = arr1[i] ^ arr2[i]; 11 arr2[i] = arr1[i] ^ arr2[i]; 12 arr1[i] = arr1[i] ^ arr2[i]; 13 14 } 15 for (i = 0; i < 9; i++){ 16 printf("%d ", arr1[i]); 17 } 18 printf(" "); 19 for (i = 0; i < 9; i++){ 20 printf("%d ", arr2[i]); 21 } 22 23 system("pause"); 24 return 0; 25 }


1348:【例4-9】城市公交网建设问题
P2024 [NOI2001]食物链
$P2573 [SCOI2012]滑雪$
$P1991 无线通讯网$
$P2872 [USACO07DEC]道路建设Building Roads$
$P1547 Out of Hay$
hdu 3468 Treasure Hunting
hungary HK 多重匹配
Hdu匹配题集