本文参考来自于:http://blog.csdn.net/wwjiang_ustc/article/details/50732211
在自然语言处理中,经常要计算单词序列(句子)出现的概率估计。我们知道,算法在训练时,语料库不可能包含所有可能出现的序列。
因此,为了防止对训练样本中未出现的新序列概率估计值为零,人们发明了好多改善估计新序列出现概率的算法,即数据平滑算法。
Laplace 法则(Add-one)
最简单的算法是Laplace法则,思路很简单,统计测试数据集中的元素在训练数据集中出现的次数时,计数器的初始值不要设成零,而是设成1。这样,即使该元素没有在训练集中出现,其出现次数统计值至少也是1。因此,其出现的概率估计值就不会是零了。
假设测试集 V 中某个元素在训练集 T 中出现 r 次,经过Laplace法则调整后的统计次数为:
当然这样做,纯粹是为了不出现零概率,并没有解决对未见过的实例进行有效预测的问题。因此,Laplace法则仅仅是一种非常初级的技术,有点太小儿科了。
Add-delta 平滑
Lidstone ’ s 不是加 1, 而是加一个小于 1 的正数,通常 = 0.5 ,此时又称为 Jeffreys-Perks Law 或 ELE 效果比 Add-one 好,但是仍然不理想 。
Good-Turing 估计
Laplace方法一个很明显的问题是 ∑r∗≠∑r。 Good-Turning 方法认为这是一个重大缺陷,需要给予改进。其实我觉得这真不算重要,只要能合理估计未见过的新实例的概率,总的统计次数发生变化又怎样呢?
Good-Turing 修正后的计算公式还真的很巧妙,它在Laplace法则后面乘了一个修正系数,就可以保证总次数不变。这个拿出来炫一炫还是没问题的:
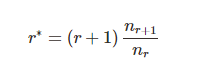
其中,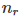 表示测试集 V 中,一共有
表示测试集 V 中,一共有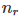 个元素在训练集 T 中出现过
个元素在训练集 T 中出现过 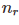 次。
次。
虽然我觉得这个方法没啥用,但是它的确保证了测试集中元素在训练集中出现的总次数不变。即:
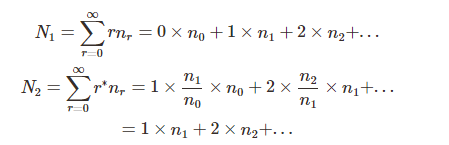
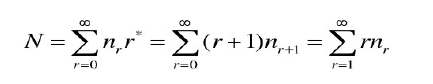


Good-Turing 估计适合单词量大并具有大量的观察数据的情况下使用,在观察数据不足的情况下,本身出现次数就是不可靠的,利用它来估计出现次数就更不可靠了。
缺乏利用低元模型对高元模型进行线性插值的思想。
显然,N1=N2。或许这个方法解决不了自然语言处理问题,而且 nr=0 时公式也会失效,但其思路应该还是很有价值的,或许解决其他问题能用得上。
缺点:(1) 无法保证概率估计的“有序性”,即出现次数多的事件的概率大于出现次数少的事件的概率。
(2) 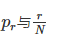 不能很好地近似,好的估计应当保证
不能很好地近似,好的估计应当保证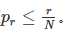
(3) 不能实现高阶模型和低阶模型的结合
优点:是其它平滑技术的基础
Backing-off 平滑
应用于大数据情况下的语言模型
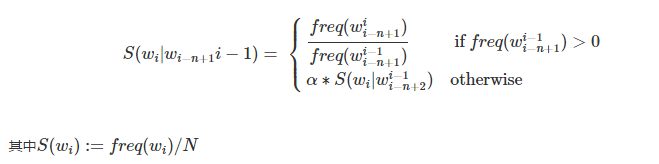
线性插值平滑
该参数平滑技术的基本思想是利用低元 n-gram 模型对高元 n-gram 模型进行线性插值。
用降元的方法来弥补高元的数据稀疏问题,数据估计有一定的可靠性。但是参数估计较困难。
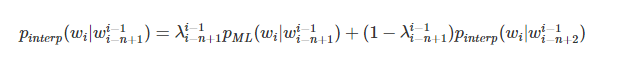
绝对折扣和线性折扣
估计发明的作者受到 Good-Turing 的刺激了,认为这个方法就是“劫富济贫”,把数量较大的统计次数拿出一部分均给了较小的统计次数,减少贫富差距。只不过这个方法用了一个很有技巧的公式掩盖的其本质。
与其羞羞答答“劫富济贫”,不如来个赤裸裸的方法,于是乎就出现了绝对折扣和线性折扣方法。
问题是,“劫富济贫”并不是我们的目的,我们需要的是能够对语料库中从未出现过的句子做出概率判断。要得到正确的判断,需要“劫”多少?“济”多少?这个问题绝对折扣和线性折扣都回答不了。所以,无论Good-Turing方法,还是这两种折扣方法,本质上都没跳出 Laplace 法则的思路。
Witten-Bell算法
Witten-Bell算法终于从 Laplace 算法跳了出来,有了质的突破。这个方法的基本思想是:如果测试过程中一个实例在训练语料库中未出现过,那么他就是一个新事物,也就是说,他是第一次出现。那么可以用在语料库中看到新实例(即第一次出现的实例)的概率来代替未出现实例的概率。
假设词汇在语料库出现的次数参见下表:

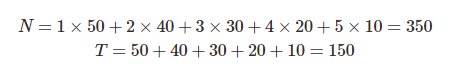
那么,我们可以用 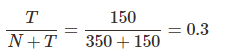 近似表示在语料库看到新词汇的概率。
近似表示在语料库看到新词汇的概率。
我不能说这个方法有多少道理,但与那些“劫富济贫”的方法相比,它至少提供了一个说得过去的理由。