题目大意:
个数,次操作
- 把修改为
- 询问区间的最大子段和
思路:
操作0很明显是可以用线段树维护的。但是问题是操作而应该如何进行操作1。
原来的只包含两个元素,现在在里面再加入四个元素。
- ,表示区间的每个点的权值之和
- ,表示区间的最大子段和
- ,表示区间的含点的最大子段和
- ,表示区间的含点的最大子段和
那么很明显,其实就是左右儿子的之和。那么就有
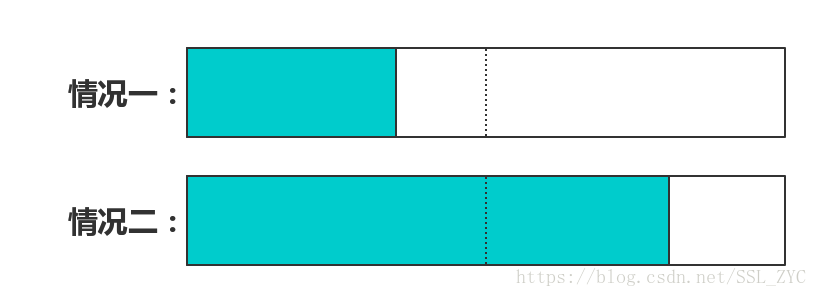
然后必须含有,那么它就有以下几种可能:
- 完全位于它的左儿子中
- 占据了全部的左儿子,并且有一部分在右儿子中,而且这部分必须在右儿子的最左边
情况一中的是,而情况二中的是(右儿子的全部和左儿子的一部分)
所以就得到了:
那么同理可得:
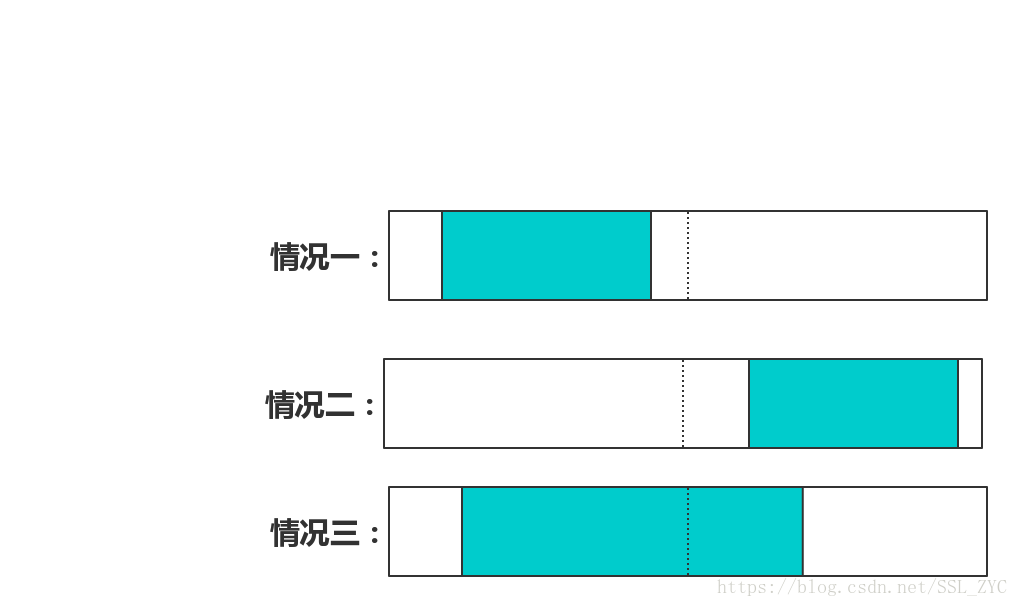
那么只要求出就可以了。很容易发现,只有三种可能:
- 完全是右儿子的最大子段和
- 完全是左儿子的最大子段和
- 既有一部分在左儿子中,又有一部分在右儿子中
所以就有:
那么我们也就维护好了最大子段和,再在每次更改中再重新更改就可以了,时间复杂度还是
代码:
#include <cstdio>
#include <algorithm>
#define N 500010
using namespace std;
int a[N];
int n,m,w,x,y,z;
struct node //线段树
{
int l,r,sum,max,lmax,rmax;
}tree[N*4];
int maxx(int x,int y,int z)
{
return max(x,max(y,z));
}
void make(int x) //建树
{
if (tree[x].l==tree[x].r) //叶子节点
{
tree[x].sum=a[tree[x].l];
tree[x].lmax=a[tree[x].l];
tree[x].rmax=a[tree[x].l];
tree[x].max=a[tree[x].l]; //只有一个可能,它本身
return;
}
int mid=(tree[x].l+tree[x].r)/2;
tree[x*2].l=tree[x].l;
tree[x*2].r=mid;
tree[x*2+1].l=mid+1;
tree[x*2+1].r=tree[x].r; //左右儿子的边界
make(x*2);
make(x*2+1);
tree[x].sum=tree[x*2].sum+tree[x*2+1].sum;
tree[x].lmax=max(tree[x*2].lmax,tree[x*2].sum+tree[x*2+1].lmax);
tree[x].rmax=max(tree[x*2+1].rmax,tree[x*2+1].sum+tree[x*2].rmax);
tree[x].max=maxx(tree[x*2].max,tree[x*2+1].max,tree[x*2].rmax+tree[x*2+1].lmax); //求出每个点的所有值
}
node find(int x,int l,int r) //查找
{
if (tree[x].l==l&&tree[x].r==r) return tree[x]; //找到
if (tree[x].l==tree[x].r) return (node){0,0,0,0,0,0}; //不成立
int mid=(tree[x].l+tree[x].r)/2;
if (r<=mid) return (node)find(x*2,l,r);
if (l>mid) return (node)find(x*2+1,l,r);
node a=find(x*2,l,mid),b=find(x*2+1,mid+1,r),c;
c.sum=a.sum+b.sum;
c.lmax=max(a.lmax,a.sum+b.lmax);
c.rmax=max(b.rmax,b.sum+a.rmax);
c.max=maxx(a.max,b.max,a.rmax+b.lmax); //求答案
return c;
}
void add(int x,int y,int k) //修改
{
if (tree[x].l==y&&tree[x].r==y) //找到
{
tree[x].sum=k;
tree[x].lmax=k;
tree[x].rmax=k;
tree[x].max=k; //重新更新
return;
}
if (tree[x].l==tree[x].r) return;
int mid=(tree[x].l+tree[x].r)/2;
if (y<=mid)
{
add(x*2,y,k);
tree[x].sum=tree[x*2].sum+tree[x*2+1].sum;
tree[x].lmax=max(tree[x*2].lmax,tree[x*2].sum+tree[x*2+1].lmax);
tree[x].rmax=max(tree[x*2+1].rmax,tree[x*2+1].sum+tree[x*2].rmax);
tree[x].max=maxx(tree[x*2].max,tree[x*2+1].max,tree[x*2].rmax+tree[x*2+1].lmax); //重新更新
}
else
{
add(x*2+1,y,k);
tree[x].sum=tree[x*2].sum+tree[x*2+1].sum;
tree[x].lmax=max(tree[x*2].lmax,tree[x*2].sum+tree[x*2+1].lmax);
tree[x].rmax=max(tree[x*2+1].rmax,tree[x*2+1].sum+tree[x*2].rmax);
tree[x].max=maxx(tree[x*2].max,tree[x*2+1].max,tree[x*2].rmax+tree[x*2+1].lmax); //重新更新
}
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
scanf("%d",&a[i]);
tree[1].l=1;
tree[1].r=n;
make(1);
scanf("%d",&m);
while (m--)
{
scanf("%d%d%d",&z,&x,&y);
if (z)
{
if (x>y) swap(x,y);
find(1,x,y);
printf("%d\n",find(1,x,y).max);
}
else
{
add(1,x,y);
}
}
return 0;
}