课后实验6--二维数组最大联通子数组的和

一、设计思想

   这次我们的题目是返回一个二维整数数组中最大联通子数组的和，在之前的基础上加了最大联通的要求。一开始是想沿用之前二维数组找矩阵最大子数组的方法，将其降维，变成一维数组之后再利用动态规划的方法找出整个二维数组的最大子数组，但是考虑到最大联通的多变性使得矩阵不容易确定，后来想起了老师在课堂上提出的另一个方法，利用图论的方法，之前在我们数据结构和离散数学课本中都有讲过，因此我们将这种方法作为了这次实验的突破点。
   这次实验的核心思想和算法就是图论中的遍历思想，以及寻找路径的方法，在遍历中在二维数组中按照优化逐个找出理想的数值相加然后比较后存入maxarray中，按照最小代价直到选出二维数组中最大的子数组的和为止。
   题目的另一个要求要有文件导入，在本次实验中实现了这个功能，用到了fstream文件输入流，方法就是写入，显示到屏幕，存入一位数组再进行遍历最后将结果显示到屏幕上，当然用户也可以选择在屏幕上输入。
   这次实验的缺点就是input.txt中二维数组中的数据只能是一位整数，因为中间有int和char的转换问题，以及循环截止的问题，因此文件的改动是有限制的，由于时间问题没有进行完善。

二、出现的问题

   在进行遍历算法求最大联通子数组和最大值的时候，在定义了数组之后，在多个函数中使用时它的引参问题，使得程序运行过程中老是出现中断的问题。后来通过结构体解决了这个问题。

   在进行文件导入，用到文件输入流时，用到了字符串写入，在编写这部分程序时在字符串存入结构体时遇到了一些问题，通过判断字符串类型解决了这个问题。

三、源程序

//二维数组最大联通子数组和最大值实验 Hao Ying CengQiqin
//2016 04 01
#include<iostream>
#include<fstream>
using namespace std;

typedef struct//建立数据结构存放二维数组以及遍历路径
{
    int traver[100];
    int Array[100][100];
    int row,column;
}Array;

int Find(Array &arr,int mul)//遍历时用来寻找代价最小的路径
{ 
    int i,j;
    for(i=1;i<=mul;i+=arr.column)
    { 
        for(j=i;j<=i+arr.column-2;j++)
        {
            arr.Array[j][j+1]=1;
            arr.Array[j+1][j]=1;
        }
    }
    for(i=1+arr.column;i<mul;i+=arr.column)
    {
        for(j=i;j<=i+arr.row-1;j++)
        {
            arr.Array[j][j-arr.column]=1;
            arr.Array[j-arr.column][j]=1;
        }
    }
    return 0;
}
int Input(Array &arr)//用于输入二维数组的函数
{
    cout<<"请输入行数："<<endl;
    cin>>arr.row;
    cout<<"请输入列数："<<endl;
    cin>>arr.column;
    cout<<"请输入一个二维数组："<<endl;
    int mul=arr.row*arr.column;
    for(int i=1;i<=mul;i++)
    {
        cin>>arr.traver[i];
    }
        return mul;
}

int MaxNum(Array &arr,int k, int traverse[], int &a, int &maxarray,int row,int mul)//遍历，找出当前的最大子数组的函数
{
    traverse[k]=1;
    maxarray+=arr.traver[k];
    if(maxarray>=a)
    {
        a=maxarray;
    }
    int k1=0,k2=0;
    for(int j1=1;j1<=mul;j1++)
    {
        for(int j2=1;j2<=mul;j2++)
        {
            if((traverse[j1]==0)&&(arr.Array[j2][j1]==1)&&(traverse[j2]==1))
            {
                k1=j1;
                k2=1; 
                break;
            }
        }
        if(k2==1)
        {
            break;
        }
    }
    for(int j1=1;j1<=mul;j1++)
    {
        for(int j2=1;j2<=mul;j2++)
        {
            if((traverse[j1]==0)&&(arr.Array[j2][j1]==1)&&(traverse[j2]==1))
            {
                if(arr.traver[k1]<arr.traver[j1])
                {
                    k1=j1;
                }
            }
        }
    }
    if(a+arr.traver[k1]<0)
    {
        arr.Array[k][k1] = 0;
    }
    else
        MaxNum(arr,k1,traverse,a,maxarray,row,mul);
    return 0;
}
int main()
{
    ifstream ifile("c:\input.txt",ios::in);//从c:input.txt文件输入数据
    Array arr;
    int p;
    cout<<"请选择输入方式：1.屏幕输入  2.文件输入  ";
    cin>>p;
    if(p==1)
    {
        Input(arr);
    }
    else if(p==2)
    {
        if(ifile.is_open()==false)
        {
            cerr<<"open error!"<<endl;
            exit(1);
        }
        cout<<"已从input.txt文件中导入数据！数据如下："<<endl;
        int p[20],u=0,s=1,c1,c2;
        char cc[20],i=0;
        ifile>>c1;
        cout<<"该数组行数："<<c1<<endl;
        arr.row=c1;
        ifile>>c2;
        cout<<"该数组列数："<<c2<<endl;
        arr.column=c2;
        cout<<"该二维数组为："<<endl;
        for(i=1;i<=18;i++)
        {
            ifile>>cc[i];
            if(cc[i]==',')
            {
                cout<<" ";
            }
            else
            {
                if(cc[i-1]=='-')
                {
                    p[s]=0-(cc[i]-48);//将文件中的负数存放起来
                    cout<<cc[i];
                    s++;
                }
                else
                {
                    if(cc[i]!='-')
                    {
                        p[s]=cc[i]-48;//将文件中的正数存放起来
                        s++;
                    }
                    cout<<cc[i];
                }
            }
            if(i%6==0)//输出矩阵
            {
                cout<<endl;
            }
        }
        ifile.close();
        for(i=1;i<=arr.row*arr.column;i++)
        {
            arr.traver[i]=p[i];//存入数据结构二维数组中
        }
    }
    else
    {
        cout<<"ERROR!"<<endl;
        return 0;
    }
    int mul=arr.row*arr.column;
    Find(arr,mul);
    int b[100]={0};
    for(int i=1;i<=mul;i++)//逐个遍历直到找到最大子数组为止
    {
        if(arr.traver[i]<0)
        {
            b[i]=arr.traver[i];
        }
        else
        {
            int traverse[100]={0};
            int maxarray=0;
            MaxNum(arr,i,traverse,b[i],maxarray,arr.row,mul);
        }
    }

    int maxarray = b[1];
    for(int i=2;i<=mul;i++)
    {
        if(b[i]>maxarray)
            maxarray=b[i];
    }
    cout<<"最大联通子数组的和为："<<maxarray<<endl;
    return 0;
}

四、结果截图

在选择使用屏幕输入时：

在选择实验input文件输入时：

input文件内容（input.txt在C盘根目录）：

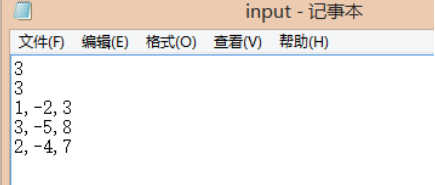
屏幕显示内容：

五、实验总结

   通过这次返回一个二维整数数组中最大联通子数组的和的实验，使我学习到了很多知识，结合上次二维数组实验，我学习到了降维的思想，在这次实验中，又学习到了图论中遍历和寻找路径的思想：在遍历中在二维数组中按照优化逐个找出理想的数值相加然后比较后存入maxarray中，按照最小代价直到选出二维数组中最大的子数组的和为止。在编写代码过程中感觉到了算法的精妙之处，虽然在中间遇到了许多的困难，比如说在定义了数组之后，在多个函数中使用时它的引参问题，使得程序运行过程中老是出现中断的问题，后来想起了使用数据结构中的结构体可以解决这个问题，也使我重新温习了一下这方面的知识。通过反复调试，最终可以输出最终结果。   

    在功能方面，一方面可以完成屏幕输入，还可以通过input文件输入，在编写这部分程序时在存入结构体时遇到了一些问题，通过判断字符串解决了这个问题，但是仍然有很多的不足，有些是我们知道的，比如文件中数据的局限性，还有一些是我们不知道的，但是不管怎么样，在这次实验中我的能力又得到了进一步的锻炼和提升，我的知识在不断的丰富和充实，相信在接下来的实验中，我会有更大的进步的！

六、工作照