二叉树学习笔记

二叉树分为斜树、满二叉树、完全二叉树

　　斜树：所有的结点都只有左子树（左斜树），或者只有右子树（右斜树）。这就是斜树，应用较少，如图

　　

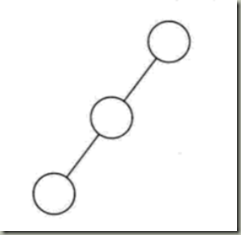
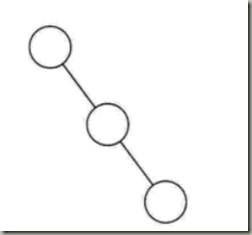
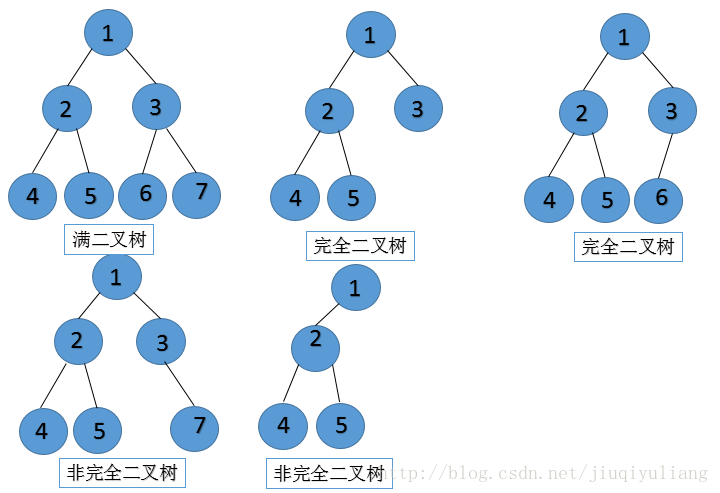
　　满二叉树：所有分支节点都存在左右子树，并且所有的叶子节点都在统一层次上，如图

　　

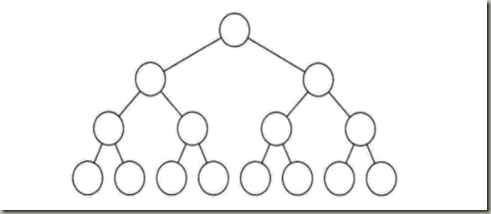
　　  根据满二叉树的定义，得到其特点为：

1. 叶子只能出现在最下一层。
2. 非叶子结点度一定是2.
3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

　　完全二叉树：对一棵具有n个结点的二叉树按层序排号，如果编号为i的结点与同样深度的满二叉树编号为i结点在二叉树中位置完全相同，（不能有节点缺失）就是完全二叉树。满二叉树必须是完全二叉树，反过来不一定成立。如图

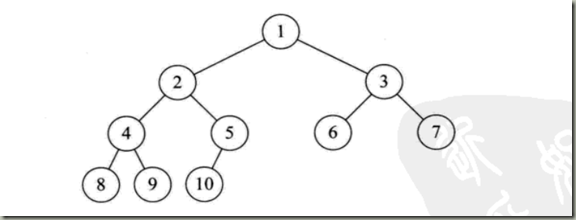　　 此树是完全二叉树

　　

二叉树性质

　　

1、在非空二叉树的i层上，至多有2^i-1个节点(i>=1)。通过归纳法论证。

2、在深度为K的二叉树上最多有2^k-1个结点（k>=1)。通过归纳法论证。

3、对于任何一棵非空的二叉树,如果叶节点个数为n₀，度数为2的节点个数为n₂，则有: n0 = n₂ + 1

证明：在一棵二叉树中，除了叶子结点（度为0）之外，就剩下度为2(n2)和1(n1)的结点了。则树的结点总数为T = n0+n1+n2;在二叉树中结点总数为T，而连线数为T-1.所以有：n0+n1+n2-1 = 2*n2 +n1;等式简化最后得到n0 = n2+1;

二叉树遍历

　　前序遍历：根->左子树->右子树

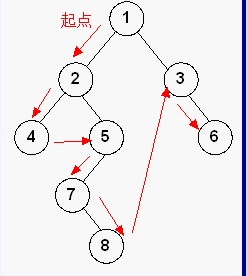
　　中序遍历：左子树->根->右子树

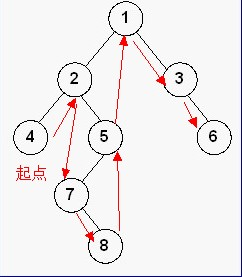
　　后续遍历：左子树->右子树->根