Leetcode刷题笔记—209Minimum Size Subarray Sum

一、问题

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组，返回 0。

示例: 

输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
进阶:

如果你已经完成了O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-size-subarray-sum

二、解决

思路1：滑动窗口：取[i  j] 区间的子数组，如果[i j]这段子数组sum<s的话，将j向后移一位使[i j]纳入一个新数字，如果还不大于s，j就继续

后移值到某一时刻大于s。

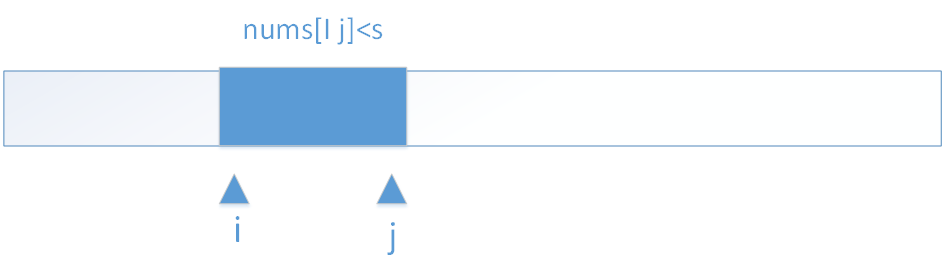
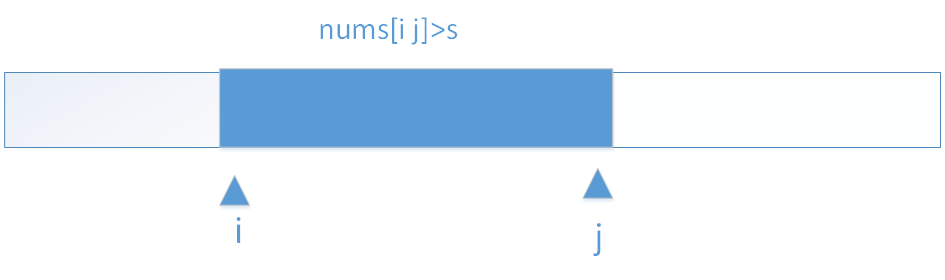
然后将i 也向后移，则子数组和不断缩小，直到某时刻又小于s，然后再去挪 j，使子数组不断增大 至某时刻又大于s。

 

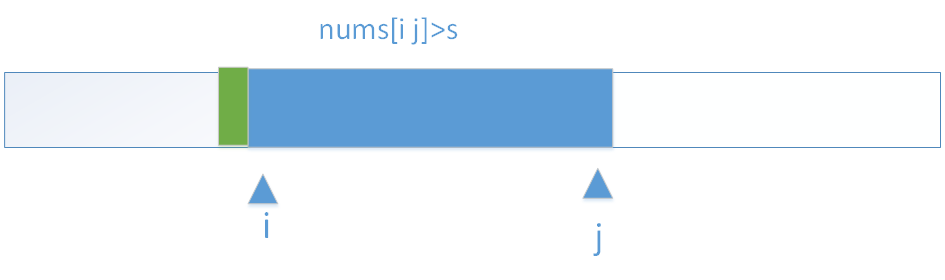
 以此类推。

 c++代码：

class Solution {

public:

    int minSubArrayLen(int s, vector<int>& nums) {

        assert(s > 0);
        int l = 0, r = -1; // 滑动窗口:nums[l...r] 因为是闭区间，所以r赋-1表示初始为空
        int sum = 0;   
        int res = nums.size() + 1;  //用于记录找到最小连续子数组的长度，初始化为nums数组长度加一
        
        while (l < nums.size()) {   // 循环条件是l索引 小于nums数组长度

            if (r + 1 < nums.size() && sum < s)// 如果sum小于s
                //因为++r要防止索引越界，所以需要在if语句中限定范围r + 1 < nums.size()
                // 如果超过这个界限 r就不能移动了，只有移动l
                sum += nums[++r];  //索引r向后移一位新纳入一位数字，然后新sum等于原sum加上新纳入的数字

            else

                sum -= nums[l++]; // 否则sum减去l索引指向的数字，然后l向后移一位。



            if (sum >= s)  // 如果sum>=s 则找到这个最小子数组

                res = min(res, r - l + 1);

        }



        if (res == nums.size() + 1)  // 无解的情况

            return 0;  // 返回 0

        return res;

    }

};

 时间复杂度O(n)，空间复杂度O(1)

代码参考：https://github.com/liuyubobobo/Play-Leetcode