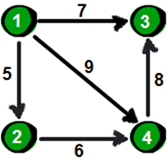
之前我们介绍过图的邻接矩阵存储法,它的空间和时间复杂度都是N2,现在我来介绍另外一种存储图的方法:邻接表,这样空间和时间复杂度就都是M。对于稀疏图来说,M要远远小于N2。先上数据,如下。
4 51 4 94 3 81 2 52 4 61 3 7
第一行两个整数n m。n表示顶点个数(顶点编号为1~n),m表示边的条数。接下来m行表示,每行有3个数x y z,表示顶点x到顶点y的边的权值为z。下图就是一种使用链表来实现邻接表的方法。
上面这种实现方法为图中的每一个顶点(左边部分)都建立了一个单链表(右边部分)。这样我们就可以通过遍历每个顶点的链表,从而得到该顶点所有的边了。使用链表来实现邻接表对于痛恨指针的的朋友来说,这简直就是噩梦。这里我将为大家介绍另一种使用数组来实现的邻接表,这是一种在实际应用中非常容易实现的方法。这种方法为每个顶点i(i从1~n)也都保存了一个类似“链表”的东西,里面保存的是从顶点i出发的所有的边,具体如下。
首先我们按照读入的顺序为每一条边进行编号(1~m)。比如第一条边“1 4 9”的编号就是1,“1 3 7”这条边的编号是5。
这里用u、v和w三个数组用来记录每条边的具体信息,即u[i]、v[i]和w[i]表示第i条边是从第u[i]号顶点到v[i]号顶点(u[i]àv[i]),且权值为w[i]。
再用一个first数组来存储每个顶点其中一条边的编号。以便待会我们来枚举每个顶点所有的边(你可能会问:存储其中一条边的编号就可以了?不可能吧,每个顶点都需要存储其所有边的编号才行吧!甭着急,继续往下看)。比如1号顶点有一条边是 “1 4 9”(该条边的编号是1),那么就将first[1]的值设为1。如果某个顶点i没有以该顶点为起始点的边,则将first[i]的值设为-1。现在我们来看看具体如何操作,初始状态如下。
咦?上图中怎么多了一个next数组,有什么作用呢?不着急,待会再解释,现在先读入第一条边“1 4 9”。
读入第1条边(1 4 9),将这条边的信息存储到u[1]、v[1]和w[1]中。同时为这条边赋予一个编号,因为这条边是最先读入的,存储在u、v和w数组下标为1的单元格中,因此编号就是1。这条边的起始点是1号顶点,因此将first[1]的值设为1。
另外这条“编号为1的边”是以1号顶点(即u[1])为起始点的第一条边,所以要将next[1]的值设为-1。也就是说,如果当前这条“编号为i的边”,是我们发现的以u[i]为起始点的第一条边,就将next[i]的值设为-1(貌似的这个next数组很神秘啊⊙_⊙)。
读入第2条边(4 3 8),将这条边的信息存储到u[2]、v[2]和w[2]中,这条边的编号为2。这条边的起始顶点是4号顶点,因此将first[4]的值设为2。另外这条“编号为2的边”是我们发现以4号顶点为起始点的第一条边,所以将next[2]的值设为-1。
读入第3条边(1 2 5),将这条边的信息存储到u[3]、v[3]和w[3]中,这条边的编号为3,起始顶点是1号顶点。我们发现1号顶点已经有一条“编号为1 的边”了,如果此时将first[1]的值设为3,那“编号为1的边”岂不是就丢失了?我有办法,此时只需将next[3]的值设为1即可。现在你知道next数组是用来做什么的吧。next[i]存储的是“编号为i的边”的“前一条边”的编号。
读入第4条边(2 4 6),将这条边的信息存储到u[4]、v[4]和w[4]中,这条边的编号为4,起始顶点是2号顶点,因此将first[2]的值设为4。另外这条“编号为4的边”是我们发现以2号顶点为起始点的第一条边,所以将next[4]的值设为-1。
读入第5条边(1 3 7),将这条边的信息存储到u[5]、v[5]和w[5]中,这条边的编号为5,起始顶点又是1号顶点。此时需要将first[1]的值设为5,并将next[5]的值改为3。
此时,如果我们想遍历1号顶点的每一条边就很简单了。1号顶点的其中一条边的编号存储在first[1]中。其余的边则可以通过next数组寻找到。请看下图。
细心的同学会发现,此时遍历边某个顶点边的时候的遍历顺序正好与读入时候的顺序相反。因为在为每个顶点插入边的时候都直接插入“链表”的首部而不是尾部。不过这并不会产生任何问题,这正是这种方法的其妙之处。
创建邻接表的代码如下。
int n,m,i;//u、v和w的数组大小要根据实际情况来设置,要比m的最大值要大1int u[6],v[6],w[6];//first和next的数组大小要根据实际情况来设置,要比n的最大值要大1int first[5],next[5];scanf("%d %d",&n,&m);//初始化first数组下标1~n的值为-1,表示1~n顶点暂时都没有边for(i=1;i<=n;i++)first[i]=-1;for(i=1;i<=m;i++){scanf("%d %d %d",&u[i],&v[i],&w[i]);//读入每一条边//下面两句是关键啦next[i]=first[u[i]];first[u[i]]=i;}
接下来如何遍历每一条边呢?我们之前说过其实first数组存储的就是每个顶点i(i从1~n)的第一条边。比如1号顶点的第一条边是编号为5的边(1 3 7),2号顶点的第一条边是编号为4的边(2 4 6),3号顶点没有出向边,4号顶点的第一条边是编号为2的边(2 4 6)。那么如何遍历1号顶点的每一条边呢?也很简单。请看下图:
遍历1号顶点所有边的代码如下。
遍历每个顶点的所有边的代码如下。k=first[1];// 1号顶点其中的一条边的编号(其实也是最后读入的边)while(k!=-1) //其余的边都可以在next数组中依次找到{printf("%d %d %d ",u[k],v[k],w[k]);k=next[k];}
for(i=1;i<=n;i++){k=first[i];while(k!=-1){printf("%d %d %d ",u[k],v[k],w[k]);k=next[k];}}
可以发现使用邻接表来存储图的时间空间复杂度是O(M),遍历每一条边的时间复杂度是也是O(M)。如果一个图是稀疏图的话,M要远小于N2。因此稀疏图选用邻接表来存储要比邻接矩阵来存储要好很多。