作者:Grey
原文地址: 最长递增子序列
问题描述
说明:这里的递增指的是严格递增,相等的时候不算递增。
暴力解法
dp[i]表示:
必须以i位置结尾的最长递增子序列是多少,如果求出了每个位置的
dp[i]值,最大的dp[i]值,就是最长递增子序列的长度
显而易见
dp[0] = 1; // 必须以0位置结尾的最长递增子序列显然是1
针对一个普遍位置i,dp[i]至少是1,那dp[i]还能扩多少呢?取决于[0,i)之间的位置j,如果arr[j] < arr[i],那么dp[i]可以是dp[j]+1。每次来到i位置,都遍历一下[0,i)之间的j位置的值是否可以和arr[i]位置连成最长递增子序列,整个暴力解法的时间复杂度是O(N^2)。暴力解法的完整代码如下:
public class LeetCode_0300_LongestIncreasingSubsequence {
// 暴力解(O(N^2))
public static int lengthOfLIS(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
if (arr.length == 1) {
return 1;
}
int max = 1;
int[] dp = new int[arr.length];
dp[0] = 1;
for (int i = 1; i < arr.length; i++) {
// dp[i]至少是1
dp[i] = 1;
for (int j = 0; j < i; j++) {
dp[i] = Math.max(dp[i], arr[j] < arr[i] ? dp[j] + 1 : 1);
}
max = Math.max(dp[i], max);
}
return max;
}
}
O(N*logN)解法
设置两个数组,含义如下
dp数组
长度和原数组长度一样,
dp[i]表示必须以i结尾的,最长递增子序列有多长。
ends数组
长度和原数组长度一样,
ends[i]表示所有长度为i+1的递增子序列中最小结尾是什么。
举例说明
以下示例图采用Processon绘制,地址见:最长递增子序列

其中i初始指向0位置,用-表示dp和ends数组中都未填数据,开始遍历原始数组arr。
当i来到0位置,arr[i]=3,显然:dp[i]=1,此时,所有长度为0+1的递增子序列中最小结尾是3。所以ends[i]=3,i来到下一个位置1。

当i来到1位置,arr[1] = 2,用arr[1]的值去ends数组中做二分查找,找大于等于arr[1]的最左位置,即ends数组的0位置,因为ends[0] = 3表示:所有长度为1的递增子序列中的最小结尾是3,所以arr[1]=2无法成长为长度为2的递增子序列,arr[1] = 2只能成长为长度为1的最长递增子序列,将ends[0]位置的值从3改成2。ends[0]左边包含自己只有1个数,所以dp[1] = 1。i来到下一个2位置。
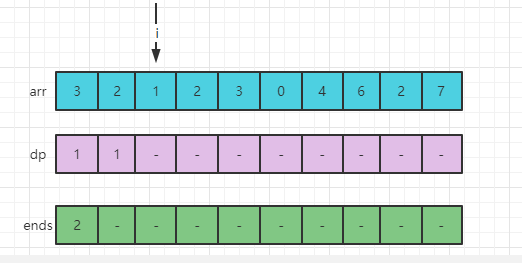
此时,arr[2] = 1,用arr[2]的值去ends数组中做二分查找,找大于等于arr[2]的最左位置,即ends数组的0位置,因为ends[0] = 2表示:所有长度为1的递增子序列中的最小结尾是2,所以arr[2]=1无法成长为长度为2的递增子序列,arr[2] = 1只能成长为长度为1的最长递增子序列,将ends[0]位置的值从2改成1。ends[0]左边包含自己只有1个数,所以dp[2] = 1。i来到下一个3位置。

此时,arr[3] = 2,用arr[3]的值去ends数组中做二分查找,找大于等于arr[3]的最左位置,没有找到,则可以扩充ends数组,因为ends[0] = 1表示:所有长度为1的递增子序列中的最小结尾是1,而现在的arr[3]=2,所以arr[3]=2有资格成长为长度为2的递增子序列,设置ends[1]=2,ends[1]左边包含自己有2个比自己小的数,所以dp[3]=2,i来到下一个4位置。
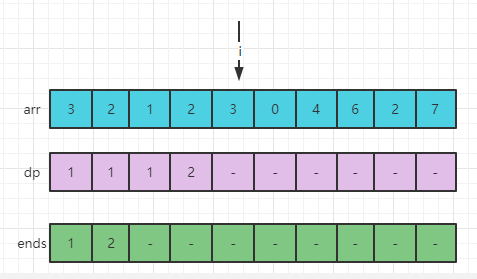
此时,arr[4] = 3,用arr[4]的值去ends数组中做二分查找,找大于等于arr[4]的最左位置,没有找到,则可以扩充ends数组,因为ends[1] = 2表示:所有长度为2的递增子序列中的最小结尾是2,而现在的arr[4]=3,所以arr[4]=3有资格成长为长度为3的递增子序列,设置ends[2]=3,ends[2]左边包含自己有3个比自己小的数,所以dp[4]=3,i来到下一个5位置。

此时,arr[5] = 0,用arr[5]的值去ends数组中做二分查找,找大于等于arr[5]的最左位置,即ends数组的0位置,因为ends[0] = 1表示:所有长度为1的递增子序列中的最小结尾是2,所以arr[5]=0无法成长为长度为2的递增子序列,arr[5] = 0只能成长为长度为1的最长递增子序列,将ends[0]位置的值从1改成0。ends[0]左边包含自己只有1个数,所以dp[5] = 1。i来到下一个6位置。
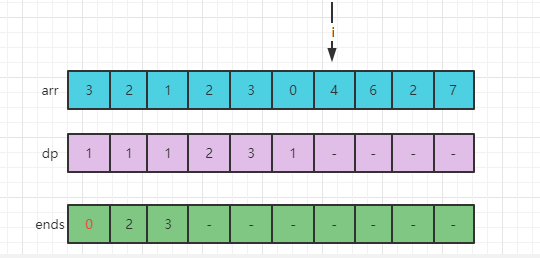
此时,arr[6] = 4,用arr[6]的值去ends数组中做二分查找,找大于等于arr[6]的最左位置,没有找到,则可以扩充ends数组,因为ends[2] = 3表示:所有长度为3的递增子序列中的最小结尾是3,而现在的arr[6]=4,所以arr[6]=4有资格成长为长度为4的递增子序列,设置ends[3]=4,ends[3]左边包含自己有4个比自己小的数,所以dp[6]=4,i来到下一个7位置。
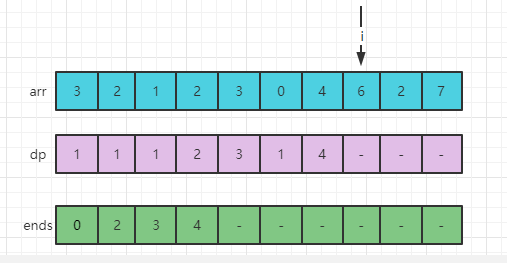
此时,arr[7] = 6,用arr[7]的值去ends数组中做二分查找,找大于等于arr[7]的最左位置,没有找到,则可以扩充ends数组,因为ends[3] = 4表示:所有长度为4的递增子序列中的最小结尾是4,而现在的arr[7]=6,所以arr[7]=6有资格成长为长度为5的递增子序列,设置ends[4]=6,ends[4]左边包含自己有5个比自己小的数,所以dp[7]=5,i来到下一个8位置。
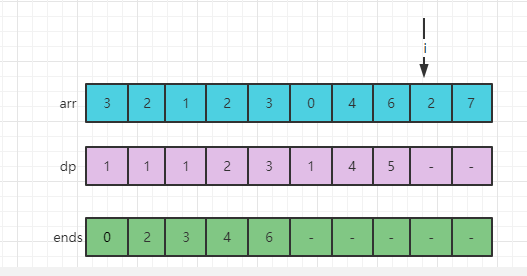
此时,arr[8] = 2,用arr[8]的值去ends数组中做二分查找,找大于等于arr[8]的最左位置,即ends数组的1位置,因为ends[1] = 2表示:所有长度为2的递增子序列中的最小结尾是2,所以arr[8]=2无法成长为长度为3的递增子序列,arr[8] = 2只能成长为长度为2的最长递增子序列,将ends[1]位置的值改成arr[8]中的这个2。ends[1]左边包含自己只有2个数,所以dp[8] = 2。i来到最后一个9位置。

arr[9] = 7,用arr[9]的值去ends数组中做二分查找,找大于等于arr[9]的最左位置,没有找到,则可以扩充ends数组,因为ends[4] = 6表示:所有长度为5的递增子序列中的最小结尾是6,而现在的arr[9]=7,所以arr[9]=7有资格成长为长度为6的递增子序列,设置ends[5]=7,ends[5]左边包含自己有6个比自己小的数,所以dp[9]=6,终止。
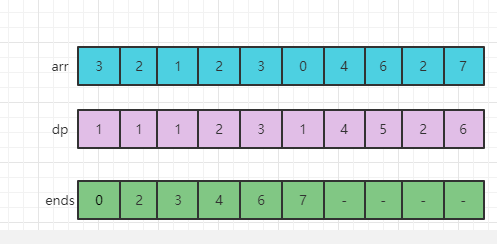
原始数组arr的最长递增子序列长度为6。
暴力解法中,来到每个i位置需要找一遍[0,i),复杂度是O(N^2),现在有了ends数组的辅助,用二分法加速了这一过程,所以,这个解法的复杂度是O(N*logN)。
完整代码如下
public class LeetCode_0300_LongestIncreasingSubsequence {
public static int lengthOfLIS(int[] arr) {
if (null == arr || arr.length == 0) {
return 0;
}
int N = arr.length;
int[] dp = new int[N];
int[] ends = new int[N];
dp[0] = 1;
ends[0] = arr[0];
int l;
int r;
int right = 0;
int max = 1;
for (int i = 0; i < N; i++) {
l = 0;
r = right;
while (l <= r) {
int m = (l + r) / 2;
if (arr[i] > ends[m]) {
l = m + 1;
} else {
r = m - 1;
}
}
right = Math.max(right, l);
dp[i] = l + 1;
ends[l] = arr[i];
max = Math.max(max, dp[i]);
}
return max;
}
}
类似问题
主要思路
信封的两个维度的数据分别依据如下规则排序:
一维从小到大,二维从大到小,然后把二维数据拿出来,最长递增子序列就是嵌套层数。
举例说明:
假设信封数据如下:[[5,4],[6,4],[6,7],[2,3]]
按照一维从小到大,二维从大到小排序后的信封如下:[[2,3],[5,4],[6,7],[6,4]]
拿出二维数据的数组如下:[3,4,7,4]
这个数组的最长递增子序列是[3,4,7], 所以返回3层。
原理:
假设信封一维从小到大,二维从大到小,然后把二维数据拿出来后的数组为[a,b,c,d,e,f,g],注:其中的字母只是抽象表示,不表示具体的数值大小。
我们调研任一位置,假设调研的位置是2号的c,根据排序策略,可以得到两个结论:
结论1:一维数据和c表示的信封一样的,二维数据不如c表示的信封的数据,一定在c的右边。这样的数据一定可以套入c里面
结论2:一维数据不如c的,二维数据也不如c的,一定在c的左边,c信封一定可以把这些数据套入
两部分内容不会干扰,所以最长递增子序列就是套的层数。