Description
Consider a tree T with N (1 <= N <= 20,000) nodes numbered 1...N. Deleting any node from the tree yields a forest: a collection of one or more trees. Define the balance of a node to be the size of the largest tree in the forest T created by deleting that node from T.
For example, consider the tree:
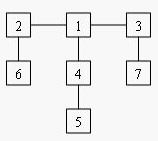
Deleting node 4 yields two trees whose member nodes are {5} and {1,2,3,6,7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2,6}, {3,7}, and {4,5}. Each of these trees has two nodes, so the balance of node 1 is two.
For each input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number.
For example, consider the tree:

Deleting node 4 yields two trees whose member nodes are {5} and {1,2,3,6,7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2,6}, {3,7}, and {4,5}. Each of these trees has two nodes, so the balance of node 1 is two.
For each input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number.
Input
The first line of input contains a single integer t (1 <= t <= 20), the number of test cases. The first line of each test case contains an integer N (1 <= N <= 20,000), the number of congruence. The next N-1 lines each contains two space-separated node numbers that are the endpoints of an edge in the tree. No edge will be listed twice, and all edges will be listed.
Output
For each test case, print a line containing two integers, the number of the node with minimum balance and the balance of that node.
Sample Input
1
7
2 6
1 2
1 4
4 5
3 7
3 1
Sample Output
1 2
这是一个模板题,是点分治的基础。我们先随便把一个结点作为根,求出siz数组,siz[i]表示以i为根的子树的大小(dfs/bfs都可以,我就用bfs了),然后去掉结点i后的最大块的大小就是max(n-siz[i],i的所有儿子中的最大siz),这样就做好了。
1 program rrr(input,output); 2 type 3 etype=record 4 t,next:longint; 5 end; 6 var 7 e:array[0..40040]of etype; 8 a,q,father,siz,f:array[0..20020]of longint; 9 v:array[0..20020]of boolean; 10 tt,i,j,n,x,y,cnt,h,t,ans,min:longint; 11 function max(a,b:longint):longint; 12 begin 13 if a>b then exit(a) else exit(b); 14 end; 15 procedure add(x,y:longint); 16 begin 17 inc(cnt);e[cnt].t:=y;e[cnt].next:=a[x];a[x]:=cnt; 18 end; 19 begin 20 assign(input,'r.in');assign(output,'r.out');reset(input);rewrite(output); 21 readln(tt); 22 for i:=1 to tt do 23 begin 24 readln(n); 25 for j:=1 to n do a[j]:=0;cnt:=0; 26 for j:=1 to n-1 do begin read(x,y);add(x,y);add(y,x); end; 27 fillchar(v,sizeof(v),false); 28 h:=0;t:=1;q[1]:=1;v[1]:=true; 29 while h<t do 30 begin 31 inc(h); 32 j:=a[q[h]]; 33 while j<>0 do 34 begin 35 if not v[e[j].t] then 36 begin 37 v[e[j].t]:=true;father[e[j].t]:=q[h]; 38 inc(t);q[t]:=e[j].t; 39 end; 40 j:=e[j].next; 41 end; 42 end; 43 for j:=1 to n do siz[j]:=1; 44 fillchar(f,sizeof(f),0);min:=n; 45 for j:=n downto 2 do 46 begin 47 t:=max(f[q[j]],n-siz[q[j]]); 48 if (t<min) or (t=min) and (q[j]<ans) then begin ans:=q[j];min:=t; end; 49 inc(siz[father[q[j]]],siz[q[j]]); 50 if siz[q[j]]>f[father[q[j]]] then f[father[q[j]]]:=siz[q[j]]; 51 end; 52 if f[1]<=min then begin ans:=1;min:=f[1]; end; 53 writeln(ans,' ',min); 54 end; 55 close(input);close(output); 56 end.