正常的欧几里得算法
1 int gcd(int a,int b){ 2 return b==0?a:gcd(b,a%b); 3 }
可以在O(n)的时间复杂度内,求出a和b两数的最大公约数。
而扩展欧几里得算法则可以在求出最大公约数的同时,求出两个数x,y,使得x*a+y*b=gcd(a,b),用处就是可以用来求解线性同余方程(写在下边)
1 //推荐第二种写法 2 #include<iostream> 3 using namespace std; 4 int exgcd1(int a,int b,int& x,int& y){ 5 if(b==0){ 6 x=1,y=0; 7 return a; 8 }else{ 9 int d=exgcd1(b,a%b,x,y); 10 int t=y; 11 y=x-(a/b)*y; 12 x=t; 13 return d; 14 } 15 } 16 int exgcd2(int a,int b,int& x,int& y){ 17 if(b==0){ 18 x=1,y=0; 19 return a; 20 }else{ 21 int d=exgcd2(b,a%b,y,x); 22 y=y-(a/b)*x; 23 return d; 24 } 25 } 26 int main(void){ 27 int n; 28 cin>>n; 29 for(int i=0;i<n;i++){ 30 int a,b,x,y; 31 cin>>a>>b; 32 exgcd2(a,b,x,y); 33 cout<<x<<" "<<y<<endl; 34 } 35 return 0; 36 }
第一种证明,第二种类似
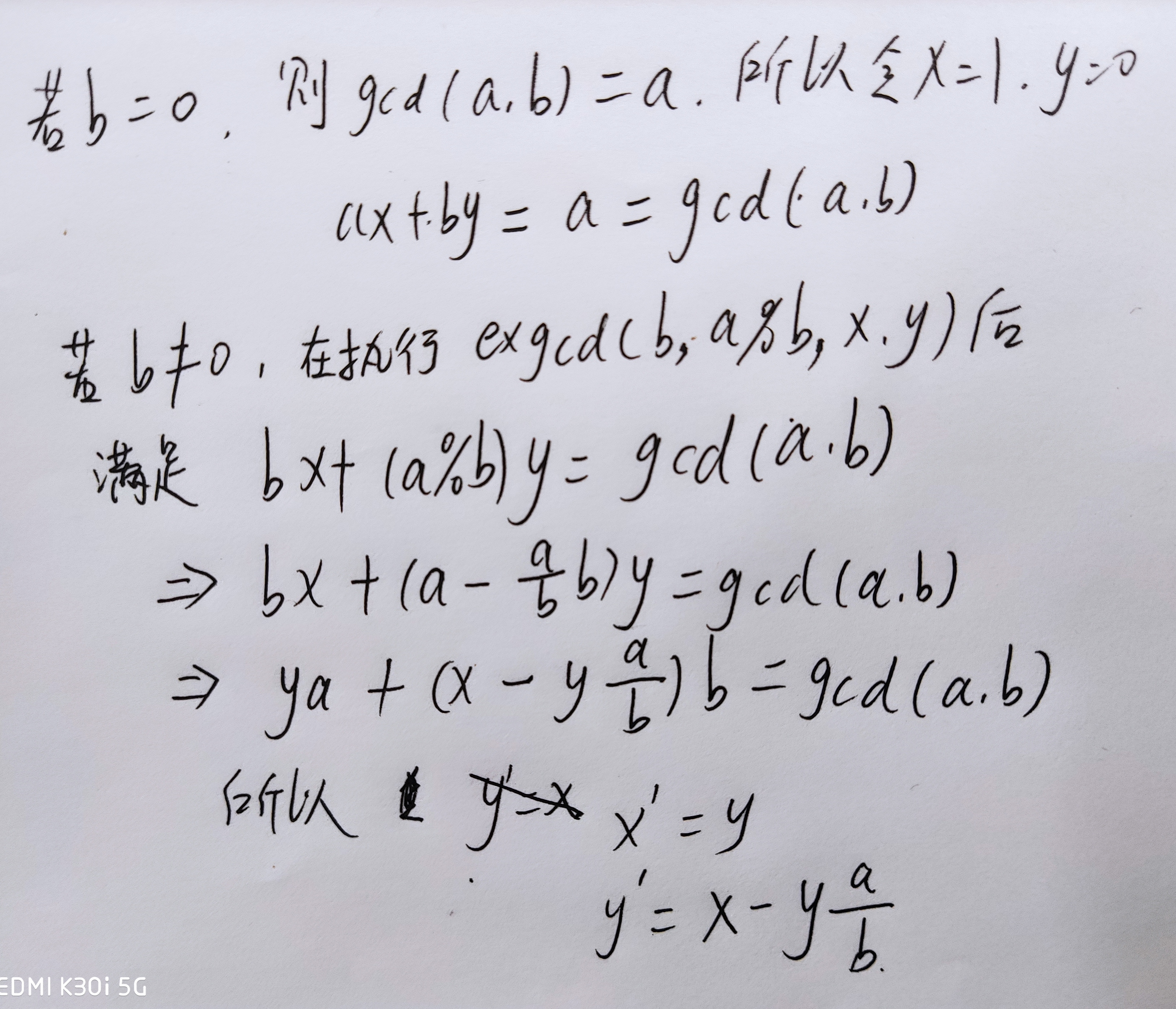
求解同余方程
同余方程的定义,给定a,b,m,求出一个满足条件的x,使得a*x=b(mod m)。
也就是a*x=b+y*m,令y′=-y,得
x*a+ y′ *m=b,这就和上边的扩展欧几里得完全符合
1 #include<iostream> 2 using namespace std; 3 typedef long long LL; 4 int exgcd(int a,int b,int& x,int& y){ 5 if(b==0){ 6 x=1,y=0; 7 return a; 8 }else{ 9 int d=exgcd(b,a%b,y,x); 10 y=y-(a/b)*x; 11 return d; 12 } 13 } 14 int main(void){ 15 int n; 16 cin>>n; 17 for(int i=0;i<n;i++){ 18 int a,b,m; 19 int x,y; 20 cin>>a>>b>>m; 21 int d=exgcd(a,m,x,y); 22 if(b%d==0){ 23 cout<<(LL)(b/d)*x%m<<endl;//%m是为了保证答案在m的范围内 24 //% m 仍然是正确的是因为,相当于将y′增加了 25 }else{ 26 cout<<"impossible"<<endl; 27 } 28 } 29 return 0; 30 }
既然能解同余方程的话,那就能够求逆元,只不过逆元是更加特殊的情况,b=1
具体的可以翻一翻博客。