There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up (u), down (d), left (l) or right (r), but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction. There is also a hole in this maze. The ball will drop into the hole if it rolls on to the hole.
Given the ball position, the hole position and the maze, find out how the ball could drop into the hole by moving the shortest distance. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the hole (included). Output the moving directions by using 'u', 'd', 'l' and 'r'. Since there could be several different shortest ways, you should output the lexicographically smallest way. If the ball cannot reach the hole, output "impossible".
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The ball and the hole coordinates are represented by row and column indexes.
Example 1
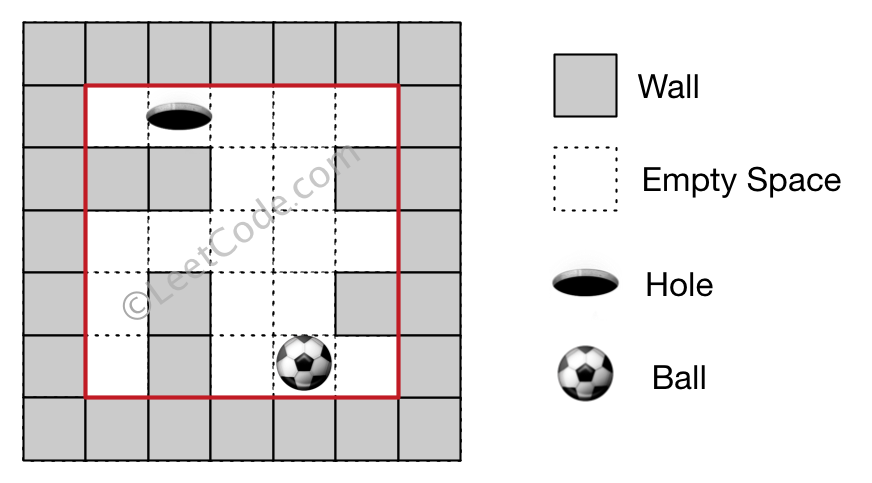
Input 1: a maze represented by a 2D array 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 Input 2: ball coordinate (rowBall, colBall) = (4, 3) Input 3: hole coordinate (rowHole, colHole) = (0, 1) Output: "lul" Explanation: There are two shortest ways for the ball to drop into the hole. The first way is left -> up -> left, represented by "lul". The second way is up -> left, represented by 'ul'. Both ways have shortest distance 6, but the first way is lexicographically smaller because 'l' < 'u'. So the output is "lul".
Example 2
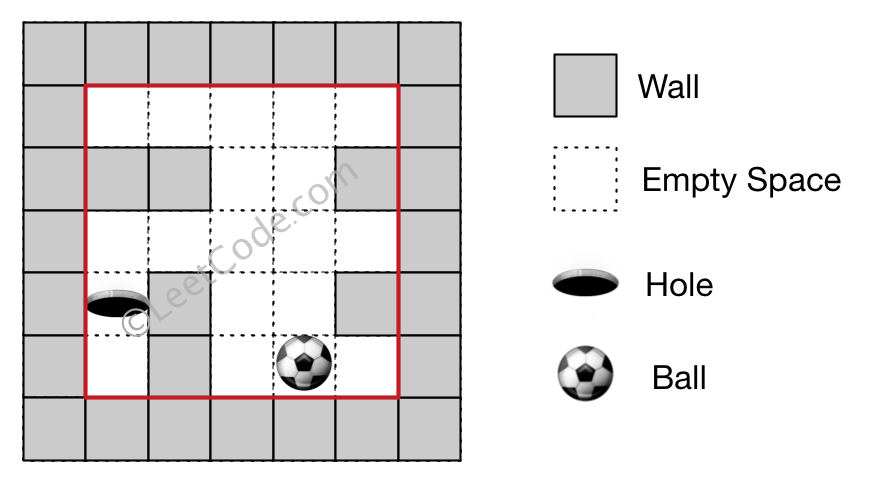
Input 1: a maze represented by a 2D array 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 Input 2: ball coordinate (rowBall, colBall) = (4, 3) Input 3: hole coordinate (rowHole, colHole) = (3, 0) Output: "impossible" Explanation: The ball cannot reach the hole.
Note:
- There is only one ball and one hole in the maze.
- Both the ball and hole exist on an empty space, and they will not be at the same position initially.
- The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and the width and the height of the maze won't exceed 30.
这道题在之前的两道The Maze II和The Maze的基础上又做了些改变,在路径中间放了个陷阱,让球在最小步数内滚到陷阱之中,此时返回的并不是最小步数,而是滚动的方向,用u, r, d, l 这四个字母来分别表示上右下左,而且在步数相等的情况下,让我们返回按字母排序小的答案。相对于迷宫二那题来说,难度是增加了一些,但我们还是可以借鉴之前那道题的思路,我们还是需要用一个二位数组dists,其中dists[i][j]表示到达(i,j)这个位置时需要的最小步数,我们都初始化为整型最大值,在后在遍历的过程中不断用较小值来更新每个位置的步数值。我们还需要用一个哈希表来建立每个位置跟滚到该位置的方向字符串之间的映射,这里我们用一个trick,将二维坐标转(i,j)为一个数字i*n+j,这实际上就是把二维数组拉成一维数组的操作,matlab中很常见的操作。还有需要注意的是,一滚到底的操作需要稍作修改,之前我们都是一直滚到墙里面或者界外才停止,然后做退一步处理,就是小球能滚到的位置,这里我们滚的时候要判断陷阱,如果滚到了陷阱,那么我们也停下来,注意这时候不需要做后退一步处理。然后我们还是比较当前步数是否小于dists中的原有步数,小于的话就更新dists,然后更新哈希表中的映射方向字符串,然后对于不是陷阱的点,我们加入队列queue中继续滚。另一点跟迷宫二不同的之处在于,这里还要处理另一种情况,就是当最小步数相等的时候,并且新的滚法的方向字符串的字母顺序要小于原有的字符串的时候,我们也需要更新哈希表的映射,并且判断是否需要加入队列queue中,参见代码如下:
解法一:
class Solution { public: string findShortestWay(vector<vector<int>>& maze, vector<int>& ball, vector<int>& hole) { int m = maze.size(), n = maze[0].size(); vector<vector<int>> dists(m, vector<int>(n, INT_MAX)); vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}}; vector<char> way{'l','u','r','d'}; queue<pair<int, int>> q; unordered_map<int, string> u; dists[ball[0]][ball[1]] = 0; q.push({ball[0], ball[1]}); while (!q.empty()) { auto t = q.front(); q.pop(); for (int i = 0; i < 4; ++i) { int x = t.first, y = t.second, dist = dists[x][y]; string path = u[x * n + y]; while (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == 0 && (x != hole[0] || y != hole[1])) { x += dirs[i][0]; y += dirs[i][1]; ++dist; } if (x != hole[0] || y != hole[1]) { x -= dirs[i][0]; y -= dirs[i][1]; --dist; } path.push_back(way[i]); if (dists[x][y] > dist) { dists[x][y] = dist; u[x * n + y] = path; if (x != hole[0] || y != hole[1]) q.push({x, y}); } else if (dists[x][y] == dist && u[x * n + y].compare(path) > 0) { u[x * n + y] = path; if (x != hole[0] || y != hole[1]) q.push({x, y}); } } } string res = u[hole[0] * n + hole[1]]; return res.empty() ? "impossible" : res; } };
下面这种写法是DFS的解法,可以看出来思路基本上跟上面的解法没有啥区别,写法上稍有不同,参见代码如下:
解法二:
class Solution { public: vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}}; vector<char> way{'l','u','r','d'}; string findShortestWay(vector<vector<int>>& maze, vector<int>& ball, vector<int>& hole) { int m = maze.size(), n = maze[0].size(); vector<vector<int>> dists(m, vector<int>(n, INT_MAX)); unordered_map<int, string> u; dists[ball[0]][ball[1]] = 0; helper(maze, ball[0], ball[1], hole, dists, u); string res = u[hole[0] * n + hole[1]]; return res.empty() ? "impossible" : res; } void helper(vector<vector<int>>& maze, int i, int j, vector<int>& hole, vector<vector<int>>& dists, unordered_map<int, string>& u) { if (i == hole[0] && j == hole[1]) return; int m = maze.size(), n = maze[0].size(); for (int k = 0; k < 4; ++k) { int x = i, y = j, dist = dists[x][y]; string path = u[x * n + y]; while (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == 0 && (x != hole[0] || y != hole[1])) { x += dirs[k][0]; y += dirs[k][1]; ++dist; } if (x != hole[0] || y != hole[1]) { x -= dirs[k][0]; y -= dirs[k][1]; --dist; } path.push_back(way[k]); if (dists[x][y] > dist) { dists[x][y] = dist; u[x * n + y] = path; helper(maze, x, y, hole, dists, u); } else if (dists[x][y] == dist && u[x * n + y].compare(path) > 0) { u[x * n + y] = path; helper(maze, x, y, hole, dists, u); } } } };
类似题目:
参考资料:
https://discuss.leetcode.com/topic/77116/bfs-solution-using-a-queue
https://discuss.leetcode.com/topic/77074/clear-java-accepted-dfs-solution-with-explanation
https://discuss.leetcode.com/topic/77474/similar-to-the-maze-ii-easy-understanding-java-bfs-solution