题目描述
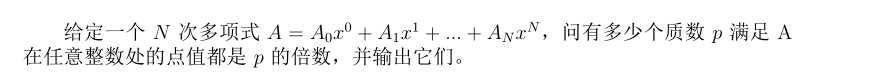

假的,n<=10^5
题解
(本题中倍数可以为负)
满足条件的p要么是|Ai|(|Ai|≠0)的gcd的约数,要么原式中存在(prod_{i=0}^{p-1}{(x-i)})
神奇结论:(prod_{i=0}^{p-1}{(x-i)}=x^p-x;(mod;p) ; p in prime)
证明: https://www.cnblogs.com/Dup4/p/10750749.html
大概是右边=x(x^(p-1)-1),根据费马小定理等于0,和左边的点值完全一致
随便枚举一下p,多项式除法O(n)判断即可
据说会卡常?
code
#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define abs(x) ((x)>0?(x):-(x))
#define ll long long
#define file
using namespace std;
ll a[100001],b[100001],s;
int p[100001],ans[200001],n,i,j,k,l,tot,len,S;
bool f[100001];
ll gcd(ll n,ll m)
{
ll r=n%m;
while (r)
n=m,m=r,r=n%m;
return m;
}
void init()
{
int i,j,k,l;
fo(i,2,n)
{
if (!f[i])
p[++len]=i;
fo(j,1,len)
if (1ll*i*p[j]<=n)
{
f[i*p[j]]=1;
if (!(i%p[j]))
break;
}
else
break;
}
}
void pd(int p)
{
int i;
fd(i,n,p)
{
b[i-p+1]=(b[i-p+1]+b[i])%p;
b[i]=0;
}
fo(i,0,n) if (b[i]) return;
ans[++tot]=p;
}
int main()
{
freopen("poly.in","r",stdin);
#ifdef file
freopen("poly.out","w",stdout);
#endif
scanf("%d",&n);
fd(i,n,0)
{
scanf("%lld",&a[i]);
if (a[i])
s=(s)?gcd(s,abs(a[i])):abs(a[i]);
}
init();
fo(i,1,len)
if (s%p[i] && !(a[0]%p[i]))
{
fo(j,0,n) b[j]=a[j]%p[i];
pd(p[i]);
}
S=floor(sqrt(s));
fo(i,2,S)
if (!(s%i))
{
ans[++tot]=i;
while (!(s%i))
s/=i;
}
if (s>1) ans[++tot]=s;
if (tot)
sort(ans+1,ans+tot+1);
fo(i,1,tot)
printf("%d
",ans[i]);
fclose(stdin);
fclose(stdout);
return 0;
}