2019年春季学期第四周作业

5-1

输入一个正整数 n (1≤n≤10)和n 阶方阵a的元素，如果方阵a中的所有元素都沿主对角线对称，输出“Yes”, 否则，输出“No”。主对角线为从矩阵的左上角至右下角的连线，方阵a中的所有元素都沿主对角线对称指对所有i, k，a[i][k]和a[k][i]相等。输入输出示例如下：

输入：

3
1 2 3
4 5 6
7 8 9

输出：

No
 
1.我的代码

#include <stdio.h>
int main(void)    
{    
       int found, i, k, n;
       int a[10][10];

       scanf ("%d", &n);
       for (i = 0; i < n; i++)    
           for (k = 0; k < n; k++)
            scanf("%d", &a[i][k]);

     found = 1;
       for (i = 0; i < n; i++){    
           for (k = 0; k < i; k++){
               if (
a[i][k]!=a[k][i]
(3分)) {    
                
found=0
;          
                           break;
                            }
        }
        if (
found==0
){
            break;
           }
      }

      if (found != 0){
          printf("Yes
");
      }  
      else{
          printf("No
");
      }  

    return 0;
}

2.设计思路

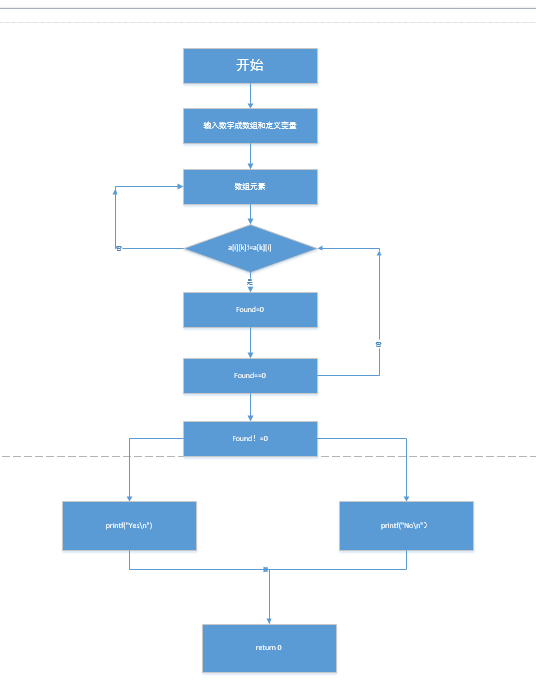
3.遇到的问题

无

4.运行结果

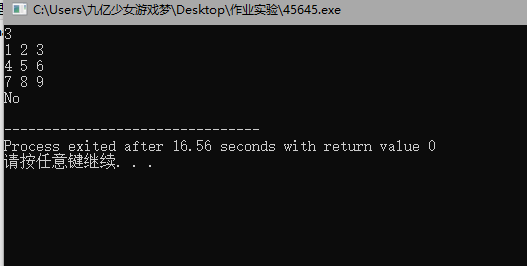
7-2 选择法排序 （20 分)

本题要求将给定的n个整数从大到小排序后输出。

输入格式：

输入第一行给出一个不超过10的正整数n。第二行给出n个整数，其间以空格分隔。

输出格式：

在一行中输出从大到小有序的数列，相邻数字间有一个空格，行末不得有多余空格。

输入样例：

4
5 1 7 6

输出样例：

7 6 5 1


1.我的代码

#include<stdio.h>
void bubble (int a [], int n);
int main()
{
  int n, a [10];
  int i;
  scanf ("%d", &n);
  for (i=0; i<n; i++)
  scanf ("%d", &a [i]);
  bubble (a, n);
  
  printf("%d",a[0]);
  for (i=1; i<n; i++)
  printf (" %d", a [i]);
  return 0;
}
void bubble (int a [], int n)
{
  int i, j, t;
  for (i=1; i<n; i++)
  for (j=0; j<n-i; j++)
  if (a [j] < a [j+1]) {
    t=a [j];
    a [j]=a [j+1];
    a [j+1]=t;
  }
}

代码是和小伙伴共同完成的。

2.遇到的问题

跟着书上的流程走没什么问题。

3.设计思路

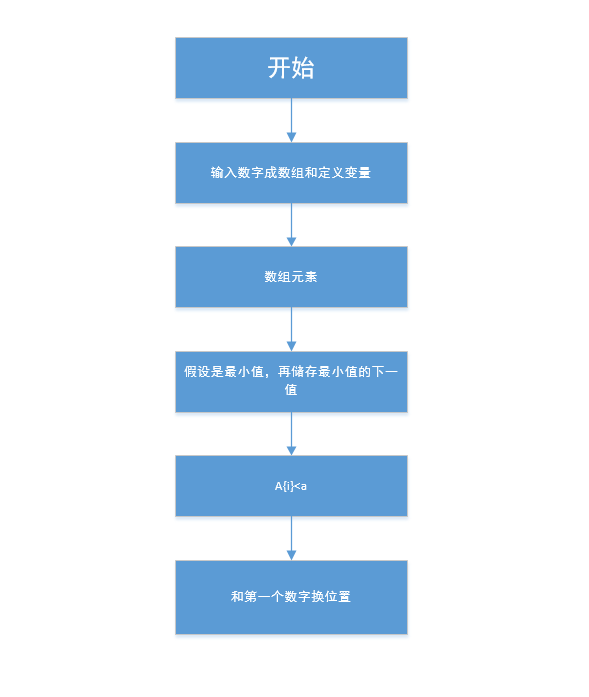
4运算结果

7-1 找鞍点 （20 分)

一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。

本题要求编写程序，求一个给定的n阶方阵的鞍点。

输入格式：

输入第一行给出一个正整数n（1≤n≤6）。随后n行，每行给出n个整数，其间以空格分隔。

输出格式：

输出在一行中按照“行下标 列下标”（下标从0开始）的格式输出鞍点的位置。如果鞍点不存在，则输出“NONE”。题目保证给出的矩阵至多存在一个鞍点。

输入样例1：

4
1 7 4 1
4 8 3 6
1 6 1 2
0 7 8 9

输出样例1：

2 1

输入样例2：

2
1 7
4 1

输出样例2：

NONE


1.我的编程

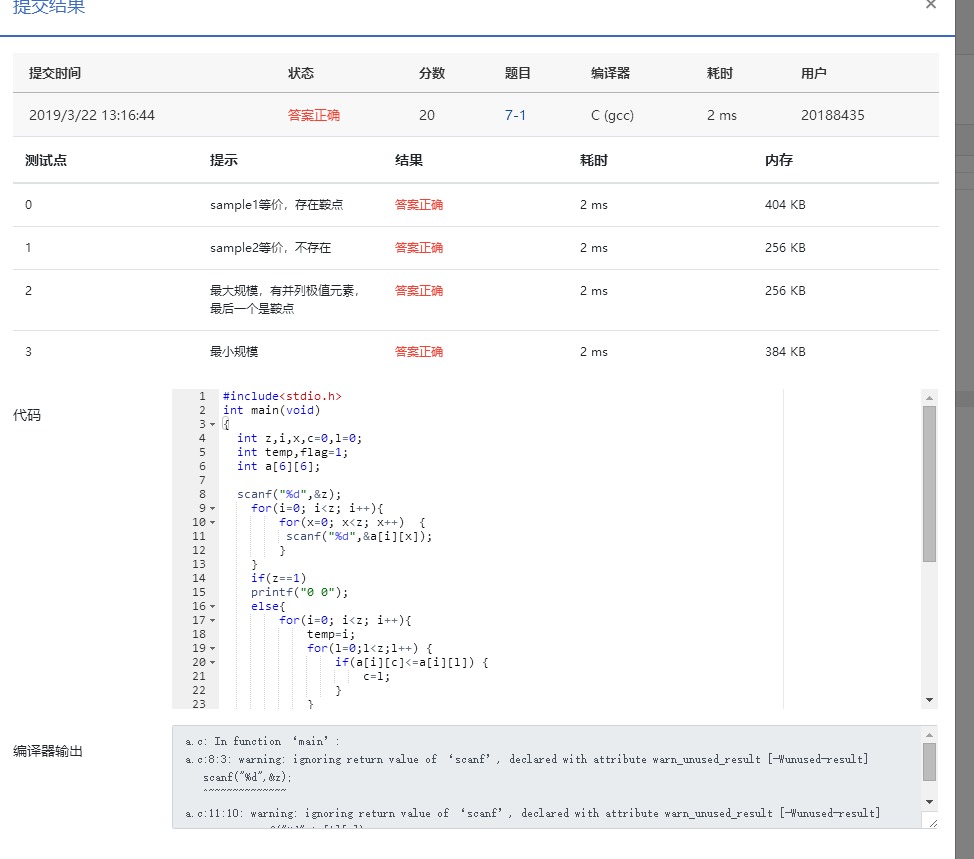
#include<stdio.h>  
int main(void)  
{       
  int z,i,x,c=0,l=0;
  int temp,flag=1;
  int a[6][6];
  
  scanf("%d",&z);
    for(i=0; i<z; i++){
        for(x=0; x<z; x++)  {  
         scanf("%d",&a[i][x]);  
        }       
    } 
    if(z==1)
    printf("0 0");
    else{  
        for(i=0; i<z; i++){  
            temp=i;   
            for(l=0;l<z;l++) {   
                if(a[i][c]<=a[i][l]) {  
                    c=l;  
                }  
            }  
            for(x=0;x<z;x++){   
                if(a[temp][c]>a[x][c]){ 
                    temp=x;  
                    break;  
                }  
            }  
            
            if(i==temp){
                flag=0;  
                break;  
            }  
        }  
        if(flag==0) 
        printf("%d %d",i,c);  
        else        
        printf("NONE");  
    }  
    return 0;
}

2.遇到的问题

懵了，至今未懂

3.运行结果

总结

周/日期	这周所花的时间	代码行	学到的知识点简介	目前比较困惑的问题
3/9-3/15	5h	132	文件建立及其文件的利用
3/15-3/18	4h	156	二位数组和暴力解法
3/18-3/19	5h	187	选择排序法	选择排序法不是特别理解