WCSPH实现方法

 在lagrange的观点里，所有的粒子carry的量都是通过一个kernel半径加权算出来的，类似于卷积方法。

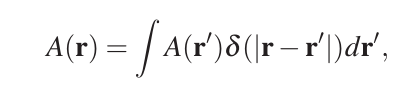
比如我要计算粒子carry的密度：

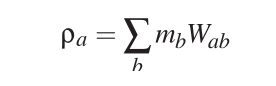
此公式与上面没有任何区别，所以最重要的如何选取一个kernel 卷积函数，而且这个kernel函数 是2阶可导。

插值可视化： 

cubic hermite smooth插值：

输入：一个线性curve，在x= [ 0 ,1] 区间，y=[0,1]区间,输入为 @P.y = @P.x;

 公式：注意只满足0-1区间。不过用数值重映射可以把函数输入的参数值输入为 真正的0-1区间。那么这个函数的导数也好求。

float smooth2(float val){
    return x*x *(3.0f - 2.0f * x);
    
};

@P.y = smooth2(@P.x);

那么这个函数导数：

// 原函数：
y = x*x *(3.0f - 2.0f * x) 
y = 3.0*x*x - 2.0f*x*x*x

// 导数为：
y' = 6*x - 5*x*x

输入：一个圆: 此概念可以扩展到高纬度， 比如输入是一个距离函数。 X Z 平面一个半径为1的⚪。

 经过反向： (p2 = {0,0,0})

float smooth2(float val) {
    return 1 - val *val *  ( 3.0f -2.0f * val);
}


vector p2 = point(1, "P", 0);
float r = distance(@P, p2);


@P.y = smooth2(r);

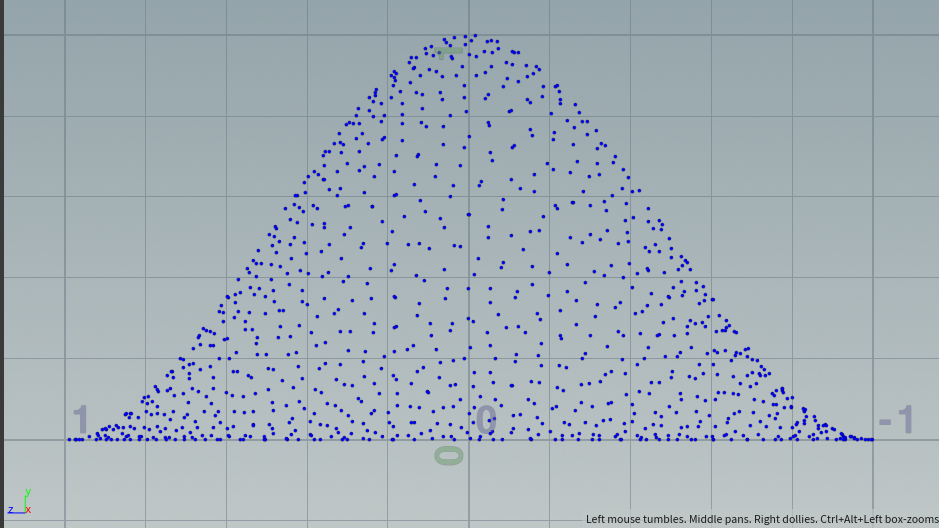
GaussKernel:

 https://staff.fnwi.uva.nl/r.vandenboomgaard/IPCV20162017/LectureNotes/IP/LocalStructure/GaussianDerivatives.html

https://homepages.inf.ed.ac.uk/rbf/HIPR2/gsmooth.htm

 

一个2d的：

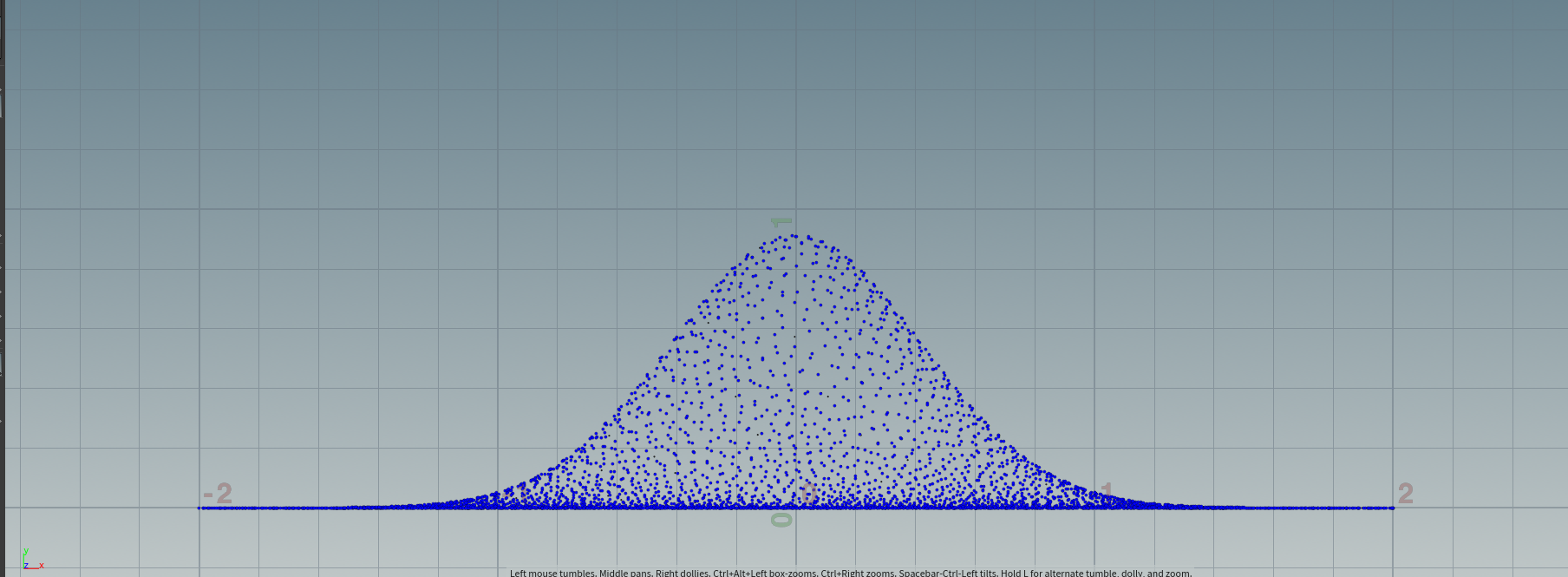
h=0.4173时候的图像

vector p2 = point(1, "P",0);
vector dir = @P - p2;
float r = dir.x*dir.x + dir.y* dir.y + dir.z * dir.z;
float h = chf("h");

float dim2_G( float r ; float h){

    float left = 1.0f / (2.0f * PI * h * h);
   
    float right = exp(- r / (2 * h * h) );
    
    return left * right;
}

float dim3_G( float r ; float h){

    float left = 1.0f / pow( ( sqrt(2.0f * PI) * h) ,3 );
   
    float right = exp(- r / (2 * h * h) );
    
    return left * right;
}

@P.y = dim3_G(r , h);

梯度：

其实上述公式可以简述，偏导数：

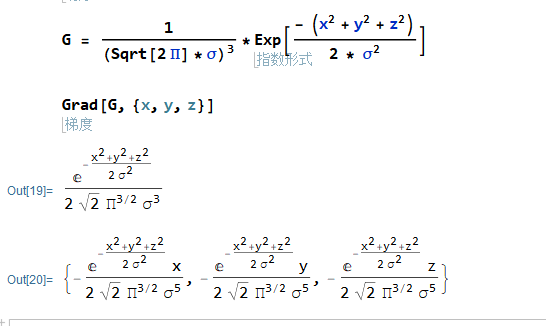
 也可以一步完成：

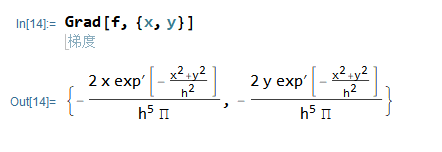
B-Cubic-Spline Kernel

(1, 2) J. Monaghan, Smoothed Particle Hydrodynamics, “Annual Review of Astronomy and Astrophysics”, 30 (1992), pp. 543-574.

https://pysph.readthedocs.io/en/latest/reference/kernels.html

 

h = 0.837 ,下图刚好看到grad方向。

 

function float Kernel(vector r ; float h){
    float q = length(r);
    q /= h;
    float factor =  1.0f / (PI  * h * h * h );

    
    if( q>0 && q<=1){
        float right =  1.0f - 1.5f  * (q * q) * (1.0f - q/ 2.0f) ;    
        return factor * right;
    }
    if(q >1 && q <=2 )
    {
        float left = factor / 4.0f;
        float right = pow(2.0f - q , 3);
        return left*right;
    }
    
    if(q>2)
    {
        return 0;
    }
    return 0;
}


function vector GradKernel(vector r; float h){
    float q = length(r);
    q /= h;
    vector dir = normalize(r);
    float factor =  1.0f / (PI  * h * h * h );
    vector retgrad = set(0,0,0);
    
    if( q<=1){
        retgrad = dir * (factor / h) * (-3.0 * q + 2.25f * q*q);
    }
    
    if( q<2){
        retgrad = dir * (-0.75f * (factor / h) * pow((2.0f - q),2) );
    }
    
    return retgrad;

}

float h = chf("h");
@P.y = Kernel(@P, h);

@N = GradKernel(@P, h);

h = 0.413 y轴的高度是density积分。

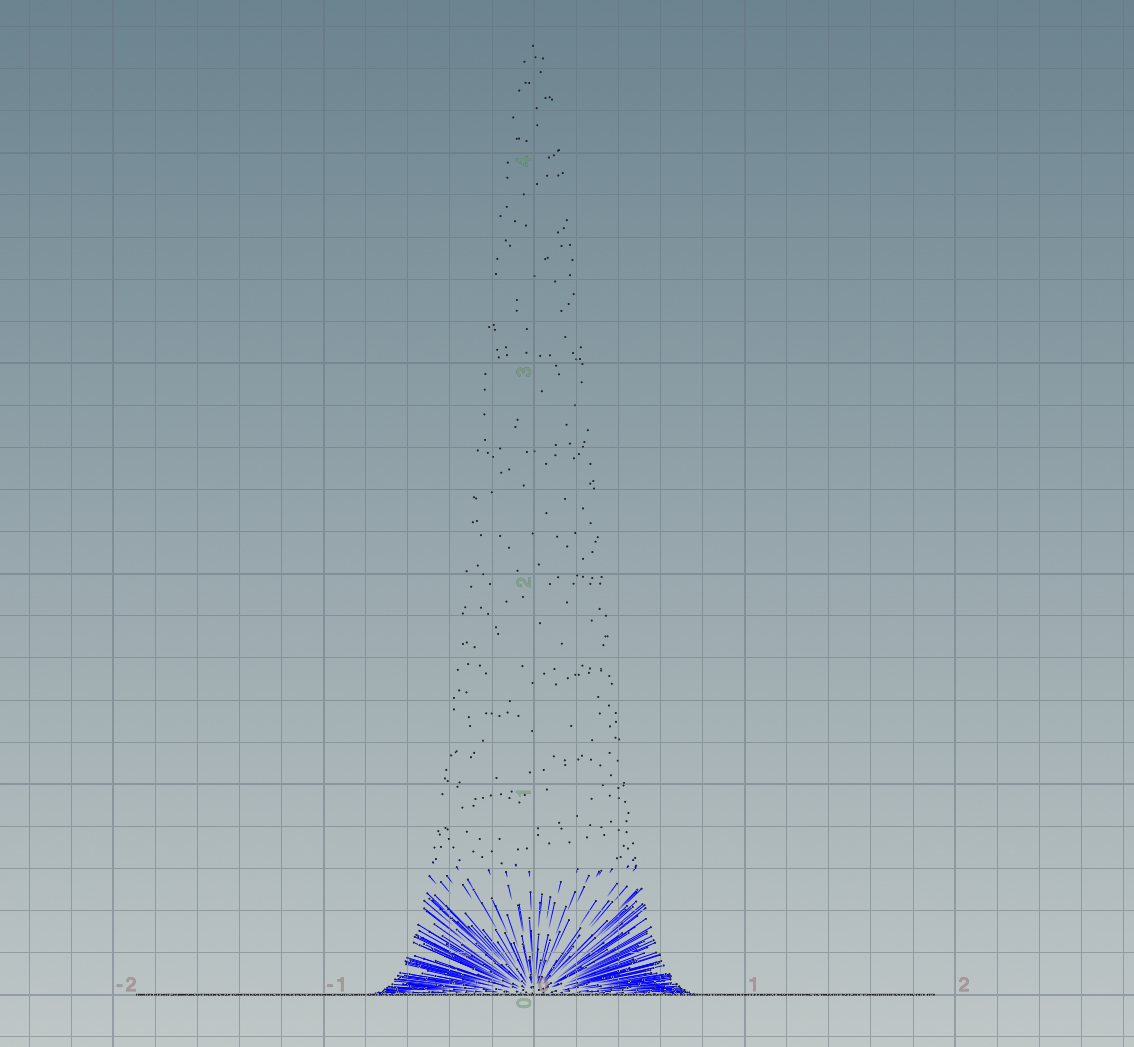
Poly6 with spiky_grandient kenel：

 

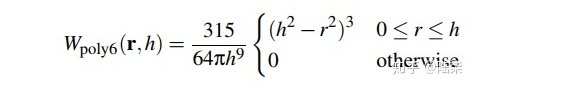
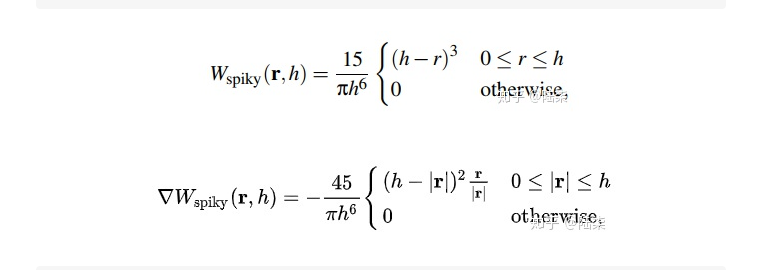
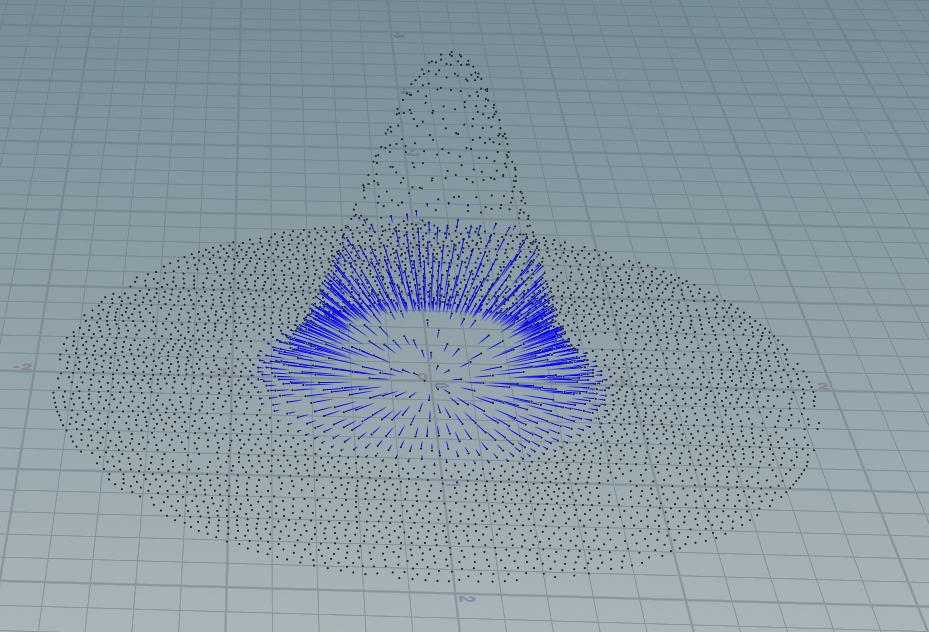
float wpoly6(float r; float h) {

    float k = 315.0f/ (64.0 * PI * pow(h,9)) ;
    float result = 0;
    if(0 < r && r <= h){
        result = k * pow(h*h - r*r , 3);
               
     }
    
    return result;
}
vector spiky_grandient(vector r; float h){
    vector result = set(0,0,0);
    float r_len = length(r);
    float k = -45.0f / (PI * pow(h,6));
    if (0 < r_len && r_len < h)
    {
    
      result = r/r_len *  k * pow(h - r_len, 2);
      
    }
    return result;
}

float r = length(@P);
float h = chf("h");

@P.y = wpoly6(r, h);
@N = spiky_grandient(@P, h);

IMP the WCSPH

Review Paper

1， 选取kernel and kernel梯度，上面的都可以选。

2，密度计算

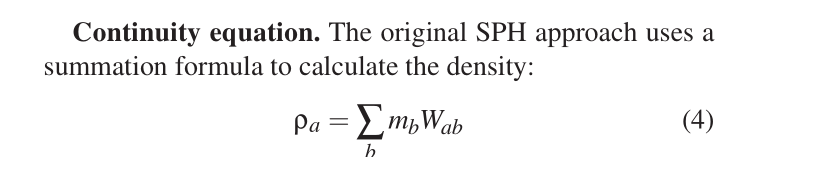
 3，根据密度计算压力

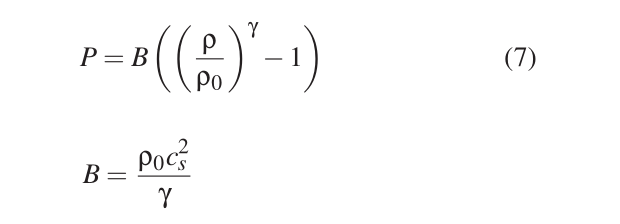
cs是sound of speed ，一般选200 

 

 

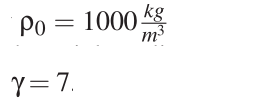
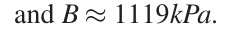
4，计算密度变化率

 5，加速度计算，求出dvdt

 6,密度加速度计算