2018-2019-1 20189221 《深入理解计算机系统》第 2 周学习总结
《深入理解计算机系统》第二章
本章讲述了计算机的算术运算,重点描绘了无符号数和数的补码表示的特性。
信息存储
计算机字长,指明指针数据的标称大小。32位机器虚拟地址空间为4GB。64位为16EB。64位机器可以运行32位机器编译的程序,反过来不行。
寻址和字节顺序:多字节对象在内存中的存放方式分为小端法和大端法。例如一个int有4个字节[x4,x3,x2,x1],x4位最高位,若x4在最前面(低地址)则为大端法,若x1在最前面则为小端法。大多数Intel兼容机都只用小端模式(也就是低地址放低位,高地址放高位)。大多数IBM的使用大端。
大小端产生的问题:1)在不同类型的机器之间通过网络传输二进制数据(用协议解决)2)在阅读表示整数数据的字节序列时。3)编写规避正常的类型系统的程序时。
字符串表示:字符串被编码为一个以null(‘�’)字符结尾的字符数组。每个字符用某个标准编码来表示,常见的为ASCII字符码。扩展有Unicode,UTF-8,其中UTF-8兼容了ASCII码。
代码表示:不同机器的指令编码是不同的,一般二进制代码是不兼容的。
布尔运算:~非,&与,|或,^异或,位运算。
逻辑运算:逻辑运算认为所有非0参数表示TRUE,0表示FALSE。对应OR(||)、AND(&&)和NOT(!)。如果第一个参数求值就能确定表达式的结果,那么逻辑运算符就不会对第二个参数求值。
移位运算:左移,x<<k,丢弃最高的k位,右端补k个零。右移分为逻辑右移和算术右移。逻辑右移在左端补0,算术右移在左端补最高位,在有符号的整数(最高位为
利用数字的算数右移,然后利用0XFF这样的数字做掩码运算,可以获取到一个数字的符号位。计算机的移位运算有一种很重要的作用就是利用掩码运算去提取一个位模式的一段信息。
C语言中的条件语句、条件运算符可以用移位的方式来做。
整数表示
无符号整数直接用其二进制数值表示。
有符号整数用补码编码,最高位为符号位,1表示负数,0为非负。负数的补码为原码的反码加1,正数的补码为本身。补码表示的范围,以4位为例,1000表示最小(-8),最大为0111(7),1111表示-1,0000表示0。
补码的范围是不对称的,|Tmin|=|Tmax|+1,C语言中文件<limits.h>定义了一组常量,来限定编译器运行时整数的范围,有INT_MAX,INT_MIN,UINT_MAX等。
为了保证程序的兼容性,ISO C99标准在文件stdint.h中引入了整数类型类,定义了如int32_t和int64_t这样恒定长度的整数类型。
在C语言中,允许强制类型转换,转换规则是数值可能会变化,位模型不变。
在进行位扩展操作的时候,比如将一个32位的有符号数扩展到64位,那么在保证原来的值不变的情况下,把31个低位扩展到64位的低位上,而最高的符号位扩展到高33位上。
将一个无符号数转换为一个更大的数据类型,直接补零就可以,这叫零扩展。将一个有符号数转换为一个更大的数据类型,补符号位,叫符号扩展。
整数运算
无符号加法:溢出直接去除高位。
有符号加法:当做无符号数进行加法,溢出直接截断。
有符号的非:-x=~x+1,即等于按位取反再加1.
有符号数的乘法:xy=(x的补码y的补码)的补码
整数乘以常数:用移位和加法以及减小来代替乘法,无论x是无符号的还是有符号的,其计算结果一致。
浮点数
浮点数表示(IEEE标准):
符号位s:复数s=1,正数s=0
尾数M:是一个二进制小数
阶码E:对浮点数加权,权重为2,可以为负数。
浮点数规格化步骤:
(1)将一个浮点数变为二进制,并且写成1.x的科学记数法形式,注意是2进制,基数是2.这样的话,小数点后面的就是尾数部分,可以在尾数部分后面补足0,如果是单精度的话,要保证尾数的一个23位。
(2)因为在计算阶码的时候会用到E = exp - Bias, 所以exp = E+ Bias。这里我要强调的是,我们在写数字的时候,所看的那个阶码就是E,比如1.00000*2^12,,那么此时12是E不是exp这个位模式所代表的值。
(3)最后把对应的三个位置上的位模式写入对应的位置即可。
浮点数运算:
(浮点数的表示不像是整数,整数是能够表示确切值的,但是浮点数却不能,它是有可能做一些四舍五入的操作的,所以只是编码,不能代表准确值,因为尾数和阶码等等都是有精度限制的,有些我们能够手写出来的浮点数,但是计算机并不一定能够表示出来。)
在浮点数运算的时候,可能会出现这样两个问题:
一是加法中,两个数的阶码不同,需要调整尾数,以便两个数的小数点能够对齐,然后相加。
二是乘法中,乘法时两乘数的指数可能都很大,存在溢出可能。所以首先计算出运算准确的结果,然后在进行舍入操作,使得结果能够控制在规定的精度内
(a)舍入操作的种类:1.向0舍入 2.无限向负无穷舍入 3.无限向正无穷舍入 4.向最近的舍入(貌似看起来是最好的办法,但是一个数在两个整数中间的时候,这种情况会出问题)5.向偶数舍入
(b)但是要注意的是,在进行带有舍入操作的运算的时候,是不能运用结合律还有分配律的。这两个数学运算定律在带有舍入操作的浮点数运算里是不适用的。
(3.14 + 1e10) - 1e10 != 3.14 + (1e10 - 1e10) 1e20 * (1e20 - 1e20) != (1e20 * 1e20) - (1e20 * 1e20)
默认的情况下,浮点数的舍入方式是向偶数舍入。
C语言中的浮点数:
第一个要点也是我很熟悉的,以前在打ACM比赛的时候老师经常强调的一点就是不要用==符号去比较浮点数,那样会出问题。事实上很多数学函数以及运算符用在浮点数上都会出现问题,所以还是要慎重的好。最好的判断两个浮点数是否相等的办法就是使用减法,如果两者的结果是一个非常非常小的量,那么就可以近似的认为这两个浮点数是相等 的。
浮点数和整数之间的转化:
从int ---> float可能会发生舍入,但是不会发生溢出
从int --> double,如果Int的值是在53位以下的(包括53位),会得到一个精确的转换。
从float --> double, 我们会得到一个精确的转换因为double的精度远远大于float的精度
从float, double -- > int,这样的转化可能会有问题,一个是从单精度浮点数到Int,由于阶码的存在,要调整尾数的尾数,所以在移位操作的时候可能会丢掉一些低有效位。并且这样的转化会按照向0舍入的操作去进行处理数据。另一个问题是浮点数可能会远远大于或者小于整型能够表示范围,因此我们把两种类型的浮点数的比整型最小值还要小的变为Tmin,并且一些在浮点数中特殊的值,我们会将它们都转化为Tmin或者Tmax。
课后习题
- 2.61

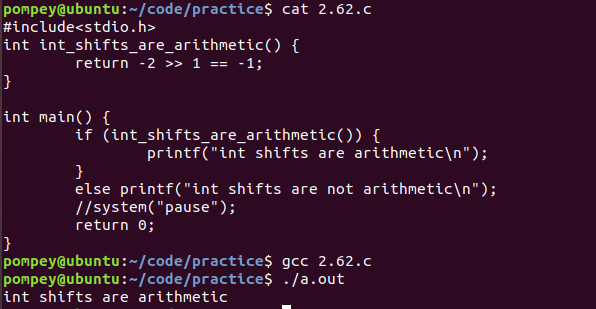
- 2.62