最小生成树的Prim算法
思想:采用子树延伸法
将顶点分成两类:
生长点——已经在生成树上的顶点
非生长点——未长到生成树上的顶点
使用待选边表:
每个非生长点在待选边表中有一条待选边,一端连着非生长点,另一端连着生长点
步骤:
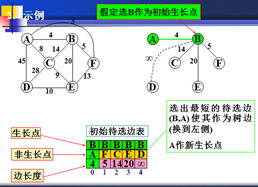
步骤1)构造初始待选边表,任选一个顶点v作为初始生长点,对其余每个非生长点w(共n-1个),将边(w,v)加进待选边表,如果边(w,v)不存在,则认为边(w,v)的长度是∞。
步骤2)循环n-2遍,非生长点个数k从n-1变到1。
①选择树边。
从待选边表中选出一条最短的待选边(u,v),这里u是非生长点,v是生长点,将(u,v)从待选边表移入生成树的边集,并且将u作为新选出的生长点。
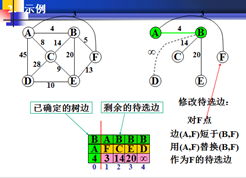
②修改待选边
对剩下的每个非生长点w,比较待选边是(w,x)与边(w,u)的长度,这里x是原有的生长点,u是新选出的生长点,如果(w,u)短于边(w,x),则用(w,u)代替(w,x),作为w的待选边;否则,什么也不做。
示例:
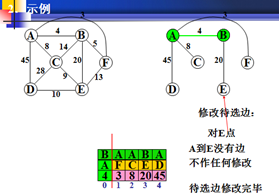



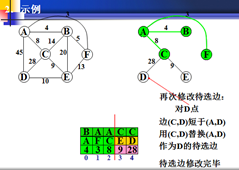


以上为官方图例,如果看不懂可以看下面的世俗图解。。。。。。。。。。。。。。。。
B为生长点,列出所有与B连接点权值。
|
B |
B |
B |
B |
B |
|
C |
A |
D |
E |
F |
|
14 |
4 |
∞ |
20 |
5 |
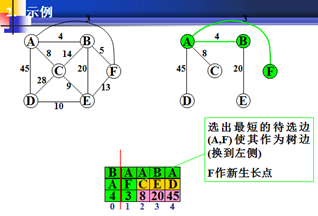
1.再以权值最小的为生长点,发现B-A的权值最小。A为新的生长点。
及B-A的边确定了。
2.A的为生长点与B原来的边进行比较,若小于原来,就交换。
A-C 8 小于 B-C 交换
A-D 45 小于 B-D 交换
A-E ∞ 大于 B-E 不交换
A-F 3 小于 B-F 交换
|
B |
A |
A |
B |
A |
|
A |
C |
D |
E |
F |
|
4 |
8 |
45 |
20 |
3 |
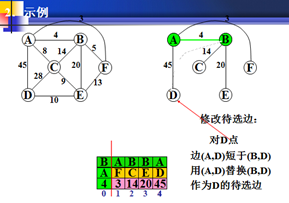
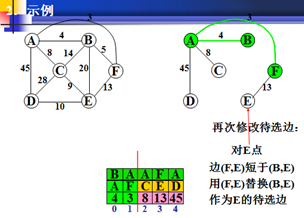
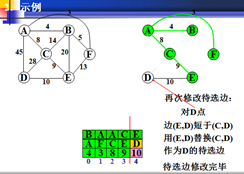
在以权值最小为生长点。F为新的生长点。
同理,F分别于A原来的权值,进行比较(如上步骤)
|
B |
A |
A |
A |
F |
|
A |
F |
C |
D |
E |
|
4 |
3 |
8 |
45 |
13 |
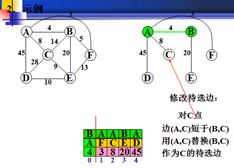
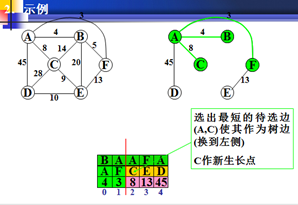
在以权值最小为生长点。C为新的生长点。
|
B |
A |
A |
C |
C |
|
A |
F |
C |
D |
E |
|
4 |
3 |
8 |
28 |
9 |
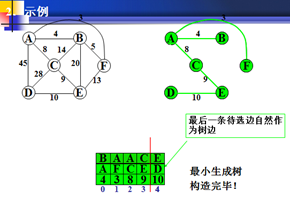
在以权值最小为生长点。E为新的生长点。
|
B |
A |
A |
C |
E |
|
A |
F |
C |
E |
D |
|
4 |
3 |
8 |
9 |
10 |
结束。按结点和权值依次画出最小生成树。
注意点:
1.要找准新的生长点(权值最小那个)。
2.找准新生长点后,要以新的生长点与各节点的权值,和原来生长点与各节点点权值,进行足一比较,小于原来的就交换。否则,保持原来的结点和权值。
实现方法分析:
(1)图的边集存储形式
采用邻接数组存储,便于比较边长度,只需存储邻接矩阵的下三角部分(无向加权图)。
(2)待选边表和树边集的存储形式
如上例,待选边表和树边集共用一个长度为n-1的数组存储,元素含3个域:生长点和非生长点名称,边长度。
(3)处理步骤(循环n-2遍)
如上例,每次从当前待选边中选出最短边作树边,换到数组左段的右端,修改剩下的待选边。
Prim算法与Kruskal算法对照:
1)主要思想——都是选短边,但选法不同
Kruskal算法从全图中选短边。
Prim算法从待选边表中选短边。
2)直观性
Kruskal采用子树合并法(直观)
Prim算采用子树延伸法
3)实现的难易程度
Kruskal算法需要判断回路(实现困难些)
Prim算法不需要判断回路
4)时间复杂性
Kruskal算法执行时间主要花费在判断回路,所需时间不超过O(mlogm),m是边数
Prim算法执行时间主要花费在n-2次修改待选边表,其时间耗费用量是O(n2)阶的,n是顶点数
Kruskal算法适用于顶点数较多,而边数较少的情况
Prim算法适用于顶点数较少,而边数较多的情况