描述
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以
从当前点走到左下方的点也可以到达右下方的点。
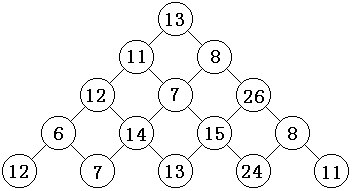
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
输入
第一个行包含R(1≤ R≤1000),表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100。
输出
单独的一行,包含那个可能得到的最大的和。
输入样例 1
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
输出样例 1
86
来源
一本通
这道题目就是一个典型的DP(动态规划)。
能用DP完成的题目有个特点:
能从局部最优解推出整体最优解。
什么意思呢?
就拿这道题来说,很明显,当这个三角形只有1层时,我们输出这个数就可以了;
当这个三角形只有2层时,我们输出上一层加上下一层的最大值就可以了。
…
这样可以推出一个结论:
每个位置能够得到的最大值,是上方和左上方中最大值与自己的和。(三角形左对齐)以此类推到第n层,把第n层的数值遍历一遍,找出其中的最大值,输出即可。
完整代码:
#include<bits/stdc++.h>
using namespace std;
int dp[1001][1001];
int main()
{
int n,ans=0;
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>dp[i][j];
}
}
if(n>1)
{
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+dp[i][j];
}
}
for(int i=1;i<=n;i++)
{
ans=max(ans,dp[n][i]);
}
cout<<ans<<endl;
}
else cout<<dp[1][1]<<endl;
return 0;
}
P.S. 因为这道题目可以用推出的DP值推出下一层的DP值,所以输入的时候也干脆直接用DP数组读入即可。。。
OV.