讲解数组之前,要了解数组的特性
1.数据具有连续性
2.数据类型相同
比如:
int Ary[3] = {0,1,2};
我们可以看出,上面定义的数组,数据是连续的,其中每个数据类型大小都是int类型(类型也是一样的)
汇编中识别数组:
1.地址连续
2.带有比例因子寻址 (lea reg32,[xxx + 4 *xxxx])
一丶一维数组在汇编中的表现形式
首先说下数组寻址公式,便于下面讲解
公式: 数组首地址 + sizeof(type) * n
伪代码:
int Ary[3] = {1,2,3};
Ary[N] = 1;
sizeof(type) : 这个是求数组元素的类型的,比如上面是int类型数组,我们求数组元素的类型 sizeof(Ary[0]);
n: n的取值是下标运算,比如我们要求第数组中的第一项,(元素为2,从零开始),
代入公式: Ary + sizeof(Ary[0]) * 1
= Ary +4 * 1
= Ary + 4 取内容则是元素2了.
看例子:
高级代码:
int main(int argc, char* argv[]) { int Ary[3] = {0,1,2}; int i = 0; scanf("%d",&i); Ary[i] = 3; //这句话会产生数组寻址公式 return Ary[i]; }
Debug下的汇编代码:
之截图重要代码

红色区域还有下面的add esp,8属于scanf上面的代码,给数组初始化等等,重要代码属于粉红框内的
1. 局部变量赋值给ecx
2.[ebp + ecx * 4 + var_c],写入了3,其中 ebp + var_c 是数组首地址, 4是sizeof(type), ecx则是n值.
由此代入我们的数组寻址公式
Ary + sizeof(type) * n
= [ebp + Var_c + 4 * ecx]
只不过比例因子寻址会变化,转为公式是一样的,其中sizeof()求出的值变为了常量.
如果喜欢汇编的这种表达形式,可以把数组公式变换一下,
变为:
Ary + (n * sizeof(type))汇编是这种的,其实是一样的.
Release下的汇编

Release下也是一样的,可能和Debug汇编不一样,但是其本质也就是数组寻址公式一样的.
Ary + sizeof(type) * n
Ary+ (n*sizeof(type))
在这里可能大家会有疑问,为什么esp + var_c是数组首地址,而不用+18h?
因为在vc6.0下,是esp寻址,而这个18h只是做调整,IDA中显示成这样是想告诉我们,我要用到Var_C,但是因为我是esp寻址,所以我要调整一下才能找到var_c
而在高版本下,则会直接ebp寻址.不重要,知道就好.
二丶二维数组在汇编下的表现形式
数组寻址公式是一样的,但不同,
1.sizeof(type)变了. type的取值变为的自己的低维
2.不光求高维,低维也要求
现在的数组寻址公式变为了:
int ary[M][C];
数组首地址 +sizeof(type[C]) * i + sizeof(type) * j; i和j是下标运算的值, 比如 ary[3][4] = 1, 3是i,j是4, 不要和MC搞混,MC是数组定义的时候的值.
其中的sizeof(type[C])变为了二维数组的低维了.
如有一个数组为:
int Ary[2][3] = {{1,2,3},{4,5,6}};
我要求4所在的位置,
我们打印的时候要输入 ary[1][0] 可以打印出4
那么我们可以通过手来计算出其位置
得出:
Ary + sizeof(type[C]) * i + sizeof(type) * j
简化公式:
Ary + C * sizeof(Type)*i + sizeof(type) * j 在Debug下会到这一步
简化公式:
ary + sizeof(type) * (i * C + j); 在Release下会优化为这一步,因为发现了公因子 sizeof(type)了,可以提出来
代入公式得到:
ary + 4 * 1 * 3 + 0
= ary + 12
也就是说数组首地址 + 12 就得出4所在的地址位置.
+12在高级语言中,因为要%4对齐,所以我们要/4
所以得出 12 / 4 = 3,那么如果是指针指向数组的首地址,那么只需要+3即可取得数组的元素4,这也是一维数组访问二维数组元素的公式.
代码:
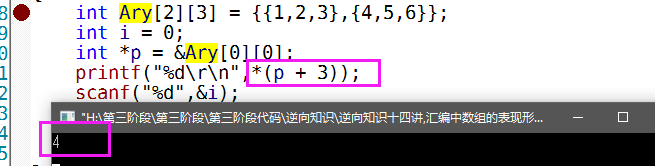
总结一下:
首先要知道数组的寻址公式,因为维数组多了一维,所以要求出高维还要求出低纬度.而其中的type取值是取自己的低维
公式; 数组首地址 + sizeof(type[C]) * i + sizeof(type)*j 重要,必须了解
举例子了解Debug下的汇编和Release下的数组寻址公式的区别
高级代码:
int main(int argc, char* argv[]) { int Ary[2][3] = {{1,2,3},{4,5,6}}; int i = 0; int j = 0; scanf("%d%d",&i,&j); Ary[i][j] = 9; //会产生数组寻址公式 return 0; }
Debug下的汇编
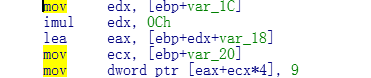
通过我们的数组寻址公式得出
1.edx 是获取i的值
2. edx * C 相当于我们的数组中的寻址公式 sizeof(type[C]) *i 的值.
3.lea的时候 求出数组首地址 + sizeof(type[c])的值.
4.ecx得出j的值
5.eax + 4 * ecx 相当于数组首地址 + sizeof(type)*j
致此熟悉数组寻址公式看汇编代码很简单了.
所以Debug下的数组公式会变成
数组首地址 + sizeof(type[C]) * i + sizeof(type] * j
Release下的汇编

上面说过,在Release下会优化我们的原始的公式为
数组首地址 + sizeof(type) * (C * i + j)的形式
我们代入到汇编中查看.
1.eax 得出i的值
2.edx得出数组首地址的值
3.ecx的出 数组首地址 + i * 2 的值
4.add eax,ecx 重新写会eax,eax = 数组首地址 + i * 2 + i 那么可以简化为数组首地址 + i * 3即可.
5.运用数组寻址公式 [esp + var18 + 4 * eax] esp + var18得出数组首地址 + i *3 + 4
因为我们的j的取值是0,所以在Release下不是我们想象的 数组首地址 + i * 3 *4 + 0,+0优化掉了.
三丶三维数组在汇编中的表现形式
其实二维数组就介绍了高维数组怎么求了,以不变应万变.
有一个三维数组
int Ary[M][C][H]
下标操作:
ary[i][j][k] = 1;
数组寻址公式为:
Ary + sizeof(type[C][H]) * i + sizeof(type[H])*j + sizeof(type)*k 在Debug下原模原样
在Release下会优化公式为:
Ary + sizeof(type)*c*h*i + sizeof(type)*h*j + sizeof(type)*k
发现公因数继续优化
Ary + sizeof(type) * (c*h*i + h*j + k)
发现了两个h
继续简化
Ary + sizeof(type) * (h*(c*i + j) + k);
所以上面就是最终公式
高级代码:
int main(int argc, char* argv[]) { int Ary[2][3][4] = {NULL}; int i = 0; int j = 0; int k = 0; scanf("%d%d%d",&i,&j,&k); Ary[i][j][k] = 9; //会产生数组寻址公式 return 0; }
Debug下的反汇编代码:
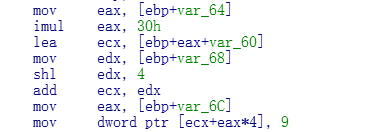
公式先贴出来:
Ary + sizeof(type[C][H]) * i + sizeof(type[H])*j + sizeof(type)*k
代入公式看汇编
1.eax = i的值
2. eax * 30 ,相当于求 sizeof(type[C][H]) * i
3.求出数组首地址+eax,也就是求出了 Ary[M]的位置,给Ecx赋值
4.求出j的值
5.左移4位,相当于2^4次方也就是16 这一步相当于求 sizeof(type[H])的值
6.ary[M] + sizeof(type[H])的值得出了 ary[M][C]的值
7.求出k的值
8.数组寻址公式 ary[M][C]的值 + 4 * k的值.
在Debug下代入公式即可.
Release下的汇编
上面说了,Release下汇编会优化,也就是我们的公式会优化.
优化为:
Ary + sizeof(type) * (h*(c*i + j) + k);
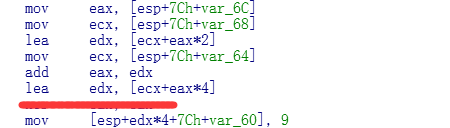
根据公式代入即可.
四维数组,高维数组,数组公式同上,只不过注意两点
1.sizeof(type) type类型比如是自己的低维
2.要加一条新的公式
比如
int ary[A][B][C][D];
下标分别为
i j k l
数组公式为:
Ary + sizeof(type[B][C][D]) * i + sizeof(type[C][D]) * j + sizeof(tyep[D]) * j + sizeof(type)*k
自己优化一下即可
总结:
数组寻址公式要熟悉最简单的数组寻址公式,因为更高纬度也是从上面公式,只不过type变化了,
会了数组寻址公式,可以说你用指针指向任何一个高维数组的值,取值使用即可.因为在高维在内存中也是线性存储,也就是一维数组的表现形式.
转载于:
作者:IBinary
出处:http://www.cnblogs.com/iBinary/