这可能是我写的最后一篇博客了....
12号了,最后一场模拟赛也落下了帷幕,终于结束了,而下一次再战就是真正的战场了...
谨以此篇祭我最后的模拟赛与我的OI生涯...
我们先看第二题吧:

考场暴毙的题...
记得以前做过类似的题,不过不敢联系他们...
其实这类题我都是好迷的,将具体的问题抽象化,不是我擅长的领域.
我们简化题意:求所有的关键点两两匹配的最大权值。上一次做的是最小值,而且所有的点都是关键题....
我们直接顺着上一次的思路想,如果求最小值,那我们可以让关键点在子树内匹配,因为出来子树要比子树内坏很多,所以我们尽可能的让点在子树内搞,实在不行才出来,很显然,出来子树一定要经过x和才能到x的父亲另找人匹配...
就像这样以u为根的子树内的关键点必须经过u到v这条边才能符合要求,这样总的对答案的贡献就是点数*1...
而这道题则要求最大,我们可以很容易的想到每个点都出来子树,这样带来的价值更大...
但我们又要考虑,如果子树外的点小于子树内的点,我们就不能让所有的点都出来,因为出来后没法匹配了,所以我们只能让部分点在子树内匹配,之后让剩下的点出来子树匹配,显然,为了让答案最大,我们让子树外的点的数量都出来匹配..
剩下的就没了,代码很简单:
#include<bits/stdc++.h> #define ll long long #define max(a,b) (a>b?a:b) #define min(a,b) (a<b?a:b) #define pb(a) push_back(a) using namespace std; const int N=100010; ll n,m,id,f[N],ans,link[N],tot,k; bool vis[N]; struct bian{int y,next;}a[N*2]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline void add(int x,int y) { a[++tot].y=y; a[tot].next=link[x]; link[x]=tot; } inline void dfs(int x,int fa) { if(vis[x]) f[x]++; for(register int i=link[x];i;i=a[i].next) { int y=a[i].y; if(y==fa) continue; dfs(y,x); f[x]+=f[y]; } if(f[x]<=k) ans+=f[x]; else ans+=2*k-f[x]; } int main() { freopen("1.in","r",stdin); n=read();k=read();id=read(); for(register int i=1,x;i<=2*k;++i) x=read(),vis[x]=1; for(register int i=1;i<n;++i) { int x=read(),y=read(); add(x,y);add(y,x); } dfs(1,0); printf("%d",ans); return 0; }
至于这类题为什么这么写,不是很懂...但仔细想想:
我们暴力求的是将每一个路径单独求解出来,然后将路径和相加,但这些思想显然没有那么具体化,他们只是在考虑每条边对答案的贡献,即这条边(如:上图中u到v)被多少个点经过,这样就不用了费时费力的枚举了...
然后分析点匹配的最优性,考虑什时候让他们经过那条边最优,这样就行了吧....
之后看第二题吧:

这个题超有信心的写了个二分+最大匹配,然后,然后就MLE了.....(呜呜呜)
这是最后一场模拟赛了,竟然还犯这种错误,这真的给我敲响了警钟...不要太掉以轻心,否则多么失望也只能接受..
都到最后还会犯MLE这种错误,那么惩罚就是但从现在开始把每一道题都当做CSP,该注意的都要注意,不能在随随便便交题了....
好了,回归这道题:
考场上注意到这应该是是个贪心,但由于我贪心的能力并不强,果断放弃,当看到每个怪只能打一次后,果断想起二分图的匹配,于是就草草的打了二分图的最大匹配去干第二题...
但除了空间问题之外,这种做法好像还会T,不知道为什么....
考后,看了某一位强者的check,使用贪心写的,真的好妙...
当给定一个答案时,我们思考如何判定,我们检查答案一定是先讨论最坏的情况,把更好的策略留给后面的人..
首先把人和怪兽坐标sort(不要问我为什么,因为这是在一维上),之后我么考虑答案的构成(人到怪兽的距离)+(怪兽到s的距离),那我们将人看成被动,兽看成主动的,排过序后针对每一个兽,他到s的距离是一定的,之后考虑到人的距离,我们会发现
只有将人和兽的坐标一一对应时才最优,否则必会造成更大的代价...

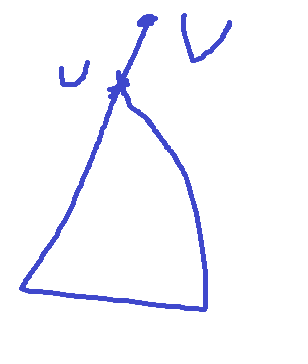
如图,圆圈代表人,三角代表怪兽,对于第三个图,第三个怪兽如果选择第一个人那么第一个怪兽无论选择2或3都会比原来选1,导致整体不是最优的,所以我们check的时候,只用用两个指针i和j扫一遍即可.
#include<bits/stdc++.h> #define ll long long #define max(a,b) (a>b?a:b) #define min(a,b) (a<b?a:b) #define pb(a) push_back(a) using namespace std; const int N=5100,qwq=1e9; int p[N],q[N],n,m,s; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline bool check(int x) { int now=1; for(register int i=1;i<=n;++i) { while(now<=m&&abs(p[i]-q[now])+abs(q[now]-s)>x) now++; if(now>m) return 0; now++; } return 1; } int main() { freopen("kill.in","r",stdin); freopen("kill.out","w",stdout); n=read();m=read();s=read(); for(register int i=1;i<=n;++i) p[i]=read(); for(register int i=1;i<=m;++i) q[i]=read(); sort(p+1,p+n+1);sort(q+1,q+m+1); int l=1,r=qwq*2; while(l<r) { int mid=(l+r)>>1; if(check(mid)) r=mid; else l=mid+1; } printf("%d",l); return 0; }
第三题正解是树剖,所以这里只讲暴力(不要问我为什么...)

有30分是n==m,显然树是个基环树,那对于不是环的边,一定在最小生成树上,则它权值可以随便变,若在环上,我们则考虑它与最大值的关系,因为它要在树上,必须删掉一个边,也就是说至少有一根边权值比他大.
那我们就找一下环的最大值和次大值,对于环上的边,如果是最大值,那最大为次大值-1,如果是次大值,则可为最大值-1...
只后有30是所有的边权为1,那我们用割边判断一下是不是必须的即可...
#include<bits/stdc++.h> #define ll long long #define max(a,b) (a>b?a:b) #define min(a,b) (a<b?a:b) #define pb(a) push_back(a) using namespace std; const int N=70010,M=100010; int f[N],dfn[N],n,m,id,link[N],tot=1,p,o,mx,mxx; int low[N]; bool vis[M*2]; struct bian{int y,next,v;}a[M*2]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline void add(int x,int y,int v) { a[++tot].y=y; a[tot].v=v; a[tot].next=link[x]; link[x]=tot; } inline void dfs(int x) { dfn[x]=++p; for(register int i=link[x];i;i=a[i].next) { int y=a[i].y; if(y==o) continue; if(!dfn[y]) f[y]=x,dfs(y); else if(y!=f[x]) { int now=x;o=x; vis[i]=1;mx=a[i].v; while(now!=y) { for(int j=link[now];j;j=a[j].next) { int v=a[j].y; if(v==f[now]) { vis[j]=1; if(a[j].v>mx) mxx=mx,mx=a[j].v; else if(a[j].v==mx) mxx=mx; else if(a[j].v<mx&&a[j].v>mxx) mxx=a[j].v; now=v;break; } } } } } } inline void solve1() { dfs(1); for(register int i=2;i<=2*m+1;i+=2) { if(!vis[i]&&!vis[i^1]) printf("-1 "); else { if(a[i].v==mx) printf("%d ",mxx-1); else printf("%d ",mx-1); } } } inline void tarjan(int x,int fa) { dfn[x]=low[x]=++p; for(register int i=link[x];i;i=a[i].next) { int y=a[i].y; if(!dfn[y]) { tarjan(y,x); low[x]=min(low[x],low[y]); if(low[y]>dfn[x]) vis[i]=vis[i^1]=1; } else if(y!=fa) low[x]=min(low[x],dfn[y]); } } inline void solve2() { for(register int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0); for(register int i=2;i<=tot;i+=2) { if(!vis[i]) printf("0 "); else printf("-1 "); } } int main() { freopen("weight.in","r",stdin); freopen("weight.out","w",stdout); n=read();m=read();id=read(); for(register int i=1;i<=m;++i) { int x=read(),y=read(),v=read(); add(x,y,v);add(y,x,v); } if(n==m) solve1(); else if(id) solve2(); return 0; }
至于调了一下午的代码,究其原因竟然是数组没开够,下次还得谨慎,因为这会影响你对算法的信心...
该开始数组还要考虑周到...
这次模拟赛是我订正最认真的一次吧,或许是最后一次了,且行且珍惜...
至于心态,我觉得比知识更重要,在这里,再安慰自己一下:
不要管别人怎么奶你的,你不是为他们比赛的,做出自己最大的努力.
尽全力,不为满足别人的期望与自己的虚荣,而是对人生的负责...
曾与别人交谈:你没得省一那就真亏了,亏了吗?难道我坚持一年只为了一纸证书???
相比于此,我觉得园神说得对:你别考虑成绩,咱们学知识知识多了一门技术,这对我们怎么来说都是有益的.要不然你整天想来想去,压力得多大呀!
这里真的真挚的感谢她,那时候我真的给自己施了太大的压力,仿佛每天真的喘不过气,大山般的压力真切的感受到了...
经她一点,仿佛重见天日,对呀,没得省一又怎么了,没拿奖我就白学编程了吗?编程带给我的难道就只能是一纸证书吗?
初学算法的艰辛,说自己不学状压,可还是硬生生的做了几道模板..
无穷无尽的debug,让我在坚韧中认真起来,让我知道了什么才是真正的永不放弃...
理性思维逐渐让我思考的更深,逐渐对人生更加合理的规划...
无论结果如何,我都享受过程了,这一路走来,我无悔!
不论结果,吾以吾血祭祭吾最后的亡魂!!!
OI生涯,青春无悔!