GANs生成对抗网络

GANs：生成对抗网络学习笔记

这一段是古德费落论文中的摘要，概括生成对抗网络。

概括:同时训练两个模型：一个产生式模型 G，该模型可以抓住数据分布；还有一个判别式模型 D 可以预测来自训练样本　而不是 G 的样本的概率．训练 G 的目的是让 D 尽可能的犯错误，让其无法判断一个图像是产生的，还是来自训练样本．这个框架对应了一个 minimax two-player game. 也就是，一方得势，必然对应另一方失势，不存在两方共赢的局面，这个就是这个游戏的规则和属性。当任意函数 G 和 D的空间，存在一个特殊的解，G 恢复出训练数据的分布，D 在任何地方都等于 1/2 。当 G 和 D 定义为 multilayer perceptrons, 整个系统可以通过 BP 算法来进行训练。在训练或者产生样本的过程中，不需要马尔科夫链 或者 unrolled approximate inference network 。

所以体现博弈过程就是生成与对抗的过程。能通过BP进行训练的原因也很简单就是两个都是神经网络。或者说多层感知机，因此可以用反向传播算法进行优化。

赶紧是竞争共赢的关系，因为彼此都达到了最好的状态。可以理解为师父在不断的鞭策徒弟使其进步。

The adversarial modeling framework 是最直接的方式, 当 models 都是多层感知机 (multilayer perceptrons) 。为了在数据 (mathrm{x}) 上学习到 generator 的分布(p_{g},) 我们在输入 noise variable (p_{z}(z)) 定义一个 prior, 然后表示到 data space 的
(Gleft(z ; heta_{g} ight)) 一个 mapping, 其中 (mathrm{G}) 是一个 differentiable function, 由多层感知机
(Dleft(x ; heta_{d} ight)) 表示。 (mathrm{D}(mathrm{x})) 表示 (mathrm{x}) 来自 (mathrm{data}) 而非 (p_{g}) 的概率。我们训练 (mathrm{D}) 来最大化赋予 training example 和 来自 G 的样本的概率。我们同时训练 G 来最小化
(log (1-D(G(z))):)换句话说, 就是 D 和 G 采用下面的 two-player minimax game with value function (mathrm{V}(mathrm{G}, mathrm{D}):)

[min _{G} max _{D} V(D, G)=mathbb{E}_{oldsymbol{x} sim p_{ ext {data }}(oldsymbol{x})}[log D(oldsymbol{x})]+mathbb{E}_{oldsymbol{z} sim p_{oldsymbol{z}}(oldsymbol{z})}[log (1-D(G(oldsymbol{z})))] ]

实际上, Equation 1 可能并没有提供足够的梯度来使得 G 学习的足够好。在学习的早期, G 是 poor 的, D 可以高置信度的方式 reject samples, 因为他们和原 始数据很明显不相同。在这种情况下, (log (1-D(G(z)))) saturates (quad) (饱和了) 。 Rather than training G to minimize (log (1-D(G(z)))), 我们可以训练G 来最大化 (log D(G(z))) 。这个目标函数 results in the same fixed point of the
dynamics of G and D but provides much stronger gradients early in learning
(在早期, 提供了非常强的梯度信息)

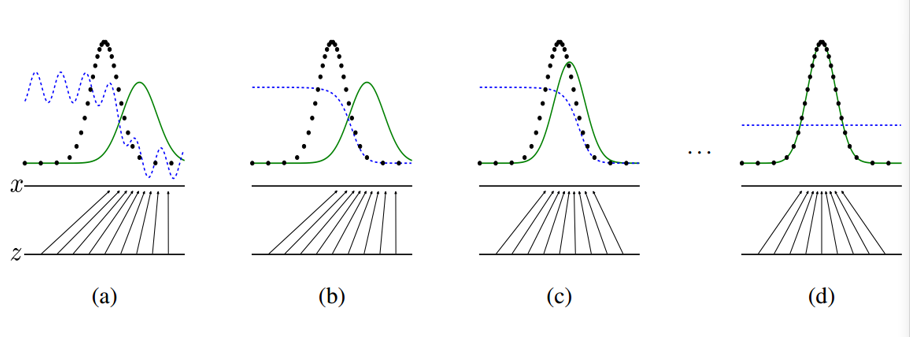
图 1. 这四个小图展示了对抗训练的过程。其中，这几条线的意思分别是：

• the discriminative distribution (D, blue, dashed line) 蓝色的虚线 表
  示判别式的分布 ;
• • • • • the data generating distribution (black, dotted line) (p_{x}) 黑色的点线表示数据产生的分布
• • • • • the generative distribution (p_{g}(G) quad) 绿色的实线
• • • • • the lower horizontal line is the domain from which z is sampled底部的水平线 是采样 z 的 domain
• • • • • the horizontal line above is part of the domain of (x). 上部的水平线 是 (mathrm{x}) domain 的部分。
• • • • • the upward arrows show the mapping (mathrm{x}=mathrm{G}(mathrm{z})) imposes the non-
          uniform distribution (p_{g}) on transformed samples. 向上的箭头展示了
          mapping (mathrm{x}=mathrm{G}(mathrm{z}),) 这个映射是非均匀分布 到 转换的samples

总的来说的步骤就是

(a) 考虑一个接近收签的 对抗 pair。 (p_{g}) 和 (p_{d a t a}) 相似; D 是一个有一定准确性的 classifier
(b) 在算法 D 的内部循环被训练用来 从数据中判断出 samples, 收签到 (D^{*}(x)=frac{p_{ ext {data}}(x)}{p_{ ext {data}}(x)+p_{g}(x)})
(c) 在更新 G 之后, D 的梯度已经引导 G(z) to flow to regions that are
more likely to be classified as data.
(d) 在几次训练之后, 如果 G 和 D 有足够的能力, 他们会达到一个平衡, 使
得两者都已经无法进一步的提升自我, 即： (p_{g}=p_{d a t a}) 。这个时候,
discriminator 已经无法判别两个分布的区别, 也就是说, 此时的 (mathrm{D}(mathrm{x})=1 / 2) 。