1635:【例 5】Strange Way to Express Integers


sol:貌似就是曹冲养猪的加强版,初看感觉非常没有思路,经过一番艰辛的***,得到以下的结果
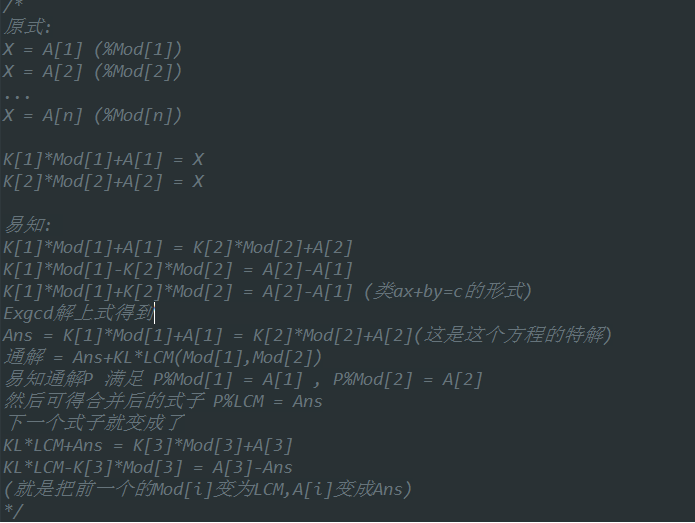
随便解释下给以后的自己听:K是要求的数字
第一个读入的A1,Mod1不用改,从2开始做,把Mod2改成LCM,A2改成Ans,接着搞3

/* 原式: X = A[1] (%Mod[1]) X = A[2] (%Mod[2]) ... X = A[n] (%Mod[n]) K[1]*Mod[1]+A[1] = X K[2]*Mod[2]+A[2] = X 易知: K[1]*Mod[1]+A[1] = K[2]*Mod[2]+A[2] K[1]*Mod[1]-K[2]*Mod[2] = A[2]-A[1] K[1]*Mod[1]+K[2]*Mod[2] = A[2]-A[1] (类ax+by=c的形式) Exgcd解上式得到 Ans = K[1]*Mod[1]+A[1] = K[2]*Mod[2]+A[2](这是这个方程的特解) 通解 = Ans+KL*LCM(Mod[1],Mod[2]) 易知通解P 满足 P%Mod[1] = A[1] , P%Mod[2] = A[2] 然后可得合并后的式子 P%LCM = Ans 下一个式子就变成了 KL*LCM+Ans = K[3]*Mod[3]+A[3] KL*LCM-K[3]*Mod[3] = A[3]-Ans (就是把前一个的Mod[i]变为LCM,A[i]变成Ans) */ #include <bits/stdc++.h> using namespace std; typedef long long ll; inline ll read() { ll s=0; bool f=0; char ch=' '; while(!isdigit(ch)) { f|=(ch=='-'); ch=getchar(); } while(isdigit(ch)) { s=(s<<3)+(s<<1)+(ch^48); ch=getchar(); } return (f)?(-s):(s); } #define R(x) x=read() inline void write(ll x) { if(x<0) { putchar('-'); x=-x; } if(x<10) { putchar(x+'0'); return; } write(x/10); putchar((x%10)+'0'); return; } #define W(x) write(x),putchar(' ') #define Wl(x) write(x),putchar(' ') const ll N=100005; int n; ll A[N],Mod[N]; inline ll gcd(ll x,ll y) { return (!y)?(x):(gcd(y,x%y)); } inline void Exgcd(ll a,ll b,ll &X,ll &Y) { if(b==0) { X=1; Y=0; return; } Exgcd(b,a%b,X,Y); ll XX=X,YY=Y; X=YY; Y=XX-a/b*YY; return; } inline ll Solve() { int i; ll a,b,c,r,X,Y,LCM=Mod[1],Ans=A[1]; for(i=2;i<=n;i++) { a=Mod[i-1]; b=Mod[i]; c=A[i]-A[i-1]; r=gcd(a,b); if(c%r) return -1; Exgcd(a,b,X=0,Y=0); X=X*c/r; ll tmp=b/r; X=(X>=0)?(X%tmp):(X%tmp+tmp); LCM=LCM*b/r; Mod[i]=LCM; Ans=X*Mod[i-1]+A[i-1]; Ans%=LCM; A[i]=Ans; } return Ans; } int main() { // freopen("2.in","r",stdin); // freopen("my.out","w",stdout); int i; while(~scanf("%d",&n)) { for(i=1;i<=n;i++) { R(Mod[i]); R(A[i]); } Wl(Solve()); } return 0; } /* input 2 8 7 11 9 output 31 input 3 91 26 62 49 95 80 3 23 9 89 80 72 15 output 409435 36303 */
