一、初识递归
1、递归的定义
在一个函数里再调用这个函数本身,这种魔性的使用函数的方式就叫做递归。
2、递归的深度
递归函数如果不受到外力的阻止会一直执行下去。每一次函数调用都会产生一个属于它自己的名称空间,如果一直调用下去,会造成名称空间占用太多内存。于是python为了杜绝类似内存溢出现象,强制将递归层数控制在了998。
def func():
print(1)
func()
func() # 递归最大深度为:998
由此可以看出,未报错之前能看到的最大数字就是997。997是python为了程序的内存优化所设定的一个默认值,可以通过一些手段修改:
# 修改递归的最大深度(尽量不要改)
import sys
sys.setrecursionlimit(1000000) # 3221
def foo(n):
print(n)
n += 1
foo(n)
foo(1)
可以通过这种方式来修改递归的最大深度,刚刚将python允许的递归深度设置为了10W,实际可以达到的深度取决于计算机的性能。不推荐修改这个默认的递归深度,如果用997层递归都没能解决的问题,要么不适合递归解决,要么代码写的太烂。
江湖流传这样一句话:人理解循环,神理解递归。
sys模块:包含所有和python相关的设置和方法。
递归就是自己调用自己。
递归需要有一个停止条件,如果没有停止条件就会报错。
二、再谈递归
例1:阶乘
6!
65432*1
def fn(n):
if n == 1:return 1
return n*fn(n-1)
print(fn(6))
执行过程:
def fn(6):
return 6*fn(5)
def fn(5):
return 5*fn(4)
def fn(4):
return 4*fn(3)
def fn(3):
return 3*fn(2)
def fn(2):
return 2*fn(1)
def fn(1):
return 1
例2:猜小明年龄
小明是新来的同学,丽丽问他多少岁了。
他说:我不告诉你,但是我比滔滔大两岁。
滔滔说:我也不告诉你,我比晓晓大两岁
晓晓说:我也不告诉你,我比小星大两岁
小星也没有告诉他说:我比小华大两岁
最后小华说,我告诉你,我今年18岁了
知道小华的,就会知道小星的,知道小星的就会知道晓晓的,以此类推,就会知道小明的年龄。这个过程接近递归思想。
- 小华 18+2
- 小星 20+2
- 晓晓 22+2
- 滔滔 24+2
- 小明 26+2
用序号表示:
age(5) = age(4)+2
age(4) = age(3) + 2
age(3) = age(2) + 2
age(2) = age(1) + 2
age(1) = 18
写成代码:
def age(n):
if n == 1:
return 18
else:
return age(n - 1) + 2
ret = age(6)
print(ret)
例3: 一个数除2,知道不能整除
def cal(num):
if num%2==0: #先判断能不能整除
num=num//2
return cal(num)
else:
return num
print(cal(8))
例4:一个数可以整除2,就整除。不能整除就*3+1
def func(num):
print(num)
if num==1:
return
if num%2==0:
num=num//2
else:
num=num*3+1
func(num)
func(5)
三、二分查找算法
# 人类的算法(灵活)
9999=99(100-1)=9900-99=9801
# 计算机的算法(死板)
99*99
计算一些比较复杂的问题,所采用的在空间上(内存里)或者时间上(执行时间)更有优势的方法
# 排序 500W个数:快速排序、堆排序、冒泡排序
# 查找
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
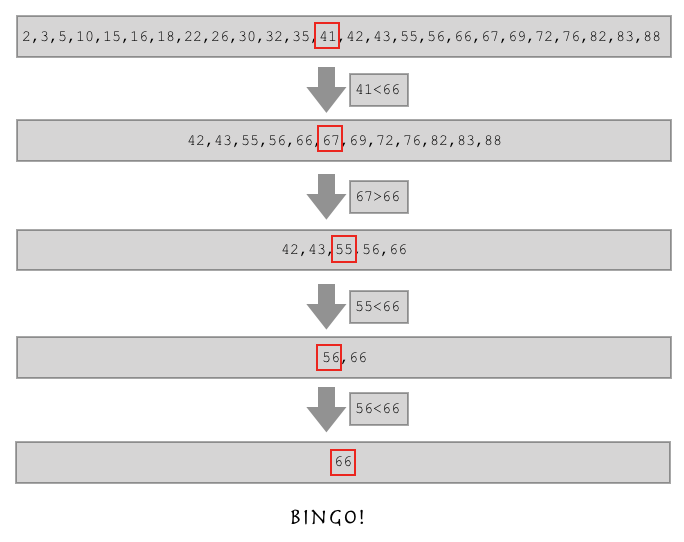
# 简单版二分法
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
def cal(l,num=66):
length = len(l)
mid = length//2
if num > l[mid]:
l = l[mid+1:]
cal(l,num)
elif num < l[mid]:
l = l[:mid]
cal(l, num)
else:
print('找到了',l[mid],mid)
cal(l,66)
# 升级版二分法
def cal(l,num,start=0,end=None):
# if end is None:end = len(l)-1
end = len(l)-1 if end is None else end
if start <= end:
mid = (end - start)//2 + start
if l[mid] > num :
return cal(l, num, start, mid-1)
elif l[mid] < num: # 13 24
return cal(l,num,mid+1,end)
else:
return mid
else:
return None
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
print(cal(l,56))