1、首先介绍一个简单的取石子游戏,规则如下:
(1)游戏参与者有两名,用A和B表示这两人
(2)有21枚石子摆成一堆
(3)两人轮流取石子,最少一枚,最多3枚
(4)两人都足够聪明,拿到最后一枚石子的玩家获胜
游戏可以逆推:
(1)当前局面无石子,上一玩家赢
(2)当前局面1-3石子,该玩家赢
(3)当前局面4石子,不管自己拿几枚石子,必输
(4)当前局面5-7石子,该玩家可把局面变成4石子,该玩家必赢
(5)当前局面8石子,不管自己拿几枚石子,给对手的局面都是对手必赢,自己必输
从上分析,当玩家面临0,4,...4n的局势,是必输的。面对着其他的局势,一定可以转化成4n的局势,自己必赢。
2、组合游戏的特点:
(1)游戏参与者有双方,且轮流行动
(2)每一方在决策的时候就能看到整个局势
(3)所有行动都将确定性的将当前局势转化成下一局势
(4)游戏开始后,一定在有限步数可以结束
3、组合游戏中的常见定义
P位置:前一玩家(Previous Player)获胜的位置
N位置:后一玩家(Next Player)获胜的位置
结束位置:由游戏规则所确定的位置,处于结束位置,不能再向其他位置移动
普通组合游戏:结束位置是P位置的组合游戏
Misere游戏:结束位置是N位置的组合游戏
4、下面只讨论普通组合游戏中P位置和N位置的计算
(1)把所有结束的位置标记为P位置
(2)一步能移动到P位置的位置标记成N位置
(3)一步只能移动到N位置的标记成P位置
(4)如果上一步没有位置标记成P位置算法结束,否则转到(2)
5、在组合游戏中P位置和N位置有如下性质:
(1)所有结束的位置都是P位置
(2)从任意一个N位置出发,通过一步一定能到达P位置
(3)从任意一个P位置出发,通过一步只能到达N位置
举例说明:
S={1,3,4},有一个n个石子的石子堆,两玩家依次取石子,取石子的数目只能是S中的某个数,取走最后一枚石子的玩家获胜。
分析:
设X为剩余石子数目,逆推这个游戏
(1)首先可知X=0为P位置

(2)X=1、3、4可以一步到达x=0的P位置,所以这些点为N位置

(3)X=2只能到达X=1的N位置,所以X=2为P位置
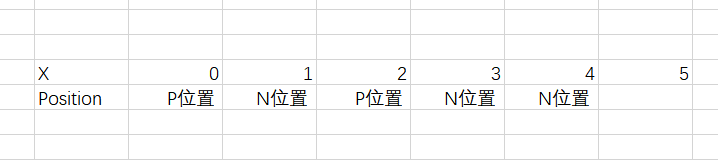
(4)X=5、6可以一步到达X=2的P位置,所以这些点为N位置

(5)X=7只能到达N位置,X=7为P位置

通过观察发现,被7整除和模7余2的位置均为P位置,其他位置为N位置(自然归纳法)
若起始位置为x=100,那么最先开始拿石子的玩家必输