问题描述
我们知道,阶乘n!表示n*(n-1)*(n-2)*......*2*1, 类似的,可以定义多阶乘计算,例如:5!!=5*3*1,依次可以有n!...!(k个‘!’,可以简单表示为n(k)!)=n*(n-k)*(n-2k)*....(直到最后一个数<=0)。
现给定一组数据n、k、m,当m=1时,计算并输出n(1)!+n(2)!+......+n(k)!的值,m=2时计算并输出n(1)!+n(2)!+......+n(k)!的各个位上的数字之和。
现给定一组数据n、k、m,当m=1时,计算并输出n(1)!+n(2)!+......+n(k)!的值,m=2时计算并输出n(1)!+n(2)!+......+n(k)!的各个位上的数字之和。
输入格式
两行,第一行为n和k,第二行为m。
输出格式
一行,为n(1)!+n(2)!+......+n(k)!的值或n(1)!+n(2)!+......+n(k)!的各个位上的数字之和。
样例输入
5 1
2
2
样例输出
3
数据规模和约定
0 < k < n <= 20
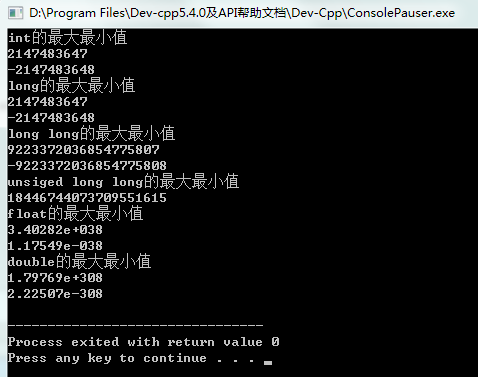
解题思路:唬人的题目,以为要上高精模板,看下数据范围,最坏的情况为n=20,k=1时,最大数为20!+19!+18!+...+1!,用long long足够存下了,以后做题先看数据范围。附上各种类型变量的最值,参考自https://blog.csdn.net/sinat_31275315/article/details/90477866。
1 #include <bits/stdc++.h>
2 using namespace std;
3 int main() {
4 cout << "int的最大最小值" << endl;
5 cout << INT_MAX << endl;
6 cout << INT_MIN << endl;
7 cout << "long的最大最小值" << endl;
8 cout << LONG_MAX << endl;
9 cout << LONG_MIN << endl;
10 cout << "long long的最大最小值" << endl;
11 cout << LONG_LONG_MAX << endl;
12 cout << LONG_LONG_MIN << endl;
13 cout << "unsiged long long的最大最小值" << endl;
14 cout << ULLONG_MAX << endl;
15 //unsigned long long 最小值为0
16 cout << "float的最大最小值" << endl;
17 cout << FLT_MAX << endl;
18 cout << FLT_MIN << endl;
19 cout << "double的最大最小值" << endl;
20 cout << DBL_MAX << endl;
21 cout << DBL_MIN << endl;
22 return 0;
23 }
1 #include <bits/stdc++.h>
2 using namespace std;
3 int main(){
4 int n, k, m;
5 cin >> n >> k >> m;
6 long long t;
7 long long ans = 0; //ans存储n(1)!+n(2)!+......+n(k)!的值
8 for (int i = 1; i <= k; i++) {
9 t = 1; //t存储n(i)!的值
10 for (int j = n; j > 0; j -= i) {
11 t *= j;
12 }
13 ans += t;
14 }
15 if (m == 1) {
16 cout << ans << endl;
17 } else {
18 int res = 0; //res存储ans这个数各个位上的数字之和
19 while (ans) {
20 res += ans % 10; //拆出每一位
21 ans /= 10;
22 }
23 cout << res << endl;
24 }
25 return 0;
26 }