大意
给定(N)个人与三个常量(A,B,C),每个人有两个属性:(Hi),(Vi).
现要让你选些人出来,定义(Hmin)为选出来的这些人中最小的(Hi)值,(Vmin)同理.
对于选出来的这些人,每个人都要满足$$Acdot Hi+Bcdot Vile Acdot Hmin+Bcdot Vmin+C$$
求最多能选出多少人。
(满足(Nle 5000))
思路
对于给出的条件,简列一下就是:
[egin{cases}
①~Acdot Hi+Bcdot Vile Acdot Hmin+Bcdot Vmin+C\
②~Hige Hmin\
③~Vige Vmin\
end{cases}]
首先,易得一个(O(N^3))的算法:暴力枚举(Hmin,Vmin),再对每个人,看是否满足以上条件。
考虑优化:
首先观察数据范围,发现支持(O(N^2))的做法。
那么先随便枚举一个(Hmin)出来(以下推导均已满足(Hminle Hi))。
考虑在枚举(Vmin)时,如何统计:
我们设(Si=Acdot Hi+Bcdot Vi),那么对于一个可以被选的点应满足
[egin{cases}
①Vige Vmin\
②Sile C+Acdot Hmin+Bcdot Vmin\
end{cases}]
发现在(Vmin)值变大的时候,式子的右边都是单调递增的。
所以我们按照(Vi)排序,再枚举一个(Vmin)出来。
然后对于一个人,我们可以这样想,把它想成二维平面上的一个点((Vi,Si))
那么就会有两个限制
[egin{cases}
①Vige Vmin\
②Sile C+Acdot Hmin+Bcdot Vmin\
end{cases}]
设有两条直线:$$L1:X=Vmin$$$$L2:Y=C+Acdot Hmin+Bcdot Vmin$$
那么在(Vmin)值变大的时候,(L1)右移,(L2)上移,如图:
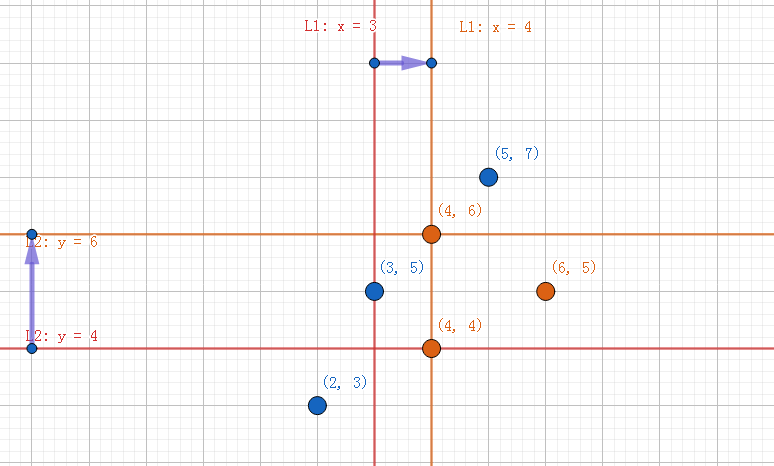
那么对应的,(L1)经过的点的(Vi)肯定都小于当前的(Vmin),故(L1)经过的都不合法。
而当前合法的点肯定会被(L2)经过。(包含当前(L2)上点)
所以,我们就可以在(Vmin)增大时,用什么Vis数组之类的动态维护答案,不断取Max值就行了。
代码
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
#define LL long long
const int MAXN=5005;
const int MAXV=10000;
int N,Ans,Vis[MAXN];
long long A,B,C;
struct Node{int H,V,id;LL S;};
Node s1[MAXN],s2[MAXN],s3[MAXN];
bool cmpH(Node X,Node Y){return X.H<Y.H;}
bool cmpV(Node X,Node Y){return X.V<Y.V;}
bool cmpS(Node X,Node Y){return X.S<Y.S;}
int main(){
//freopen("team.in","r",stdin);
//freopen("team.out","w",stdout);
scanf("%d%lld%lld%lld",&N,&A,&B,&C);
for(int i=1;i<=N;i++){
scanf("%d%d",&s1[i].H,&s1[i].V);
s1[i].S=s1[i].H*A+s1[i].V*B;s1[i].id=i;
s2[i]=s3[i]=s1[i];
}
sort(s2+1,s2+N+1,cmpV);
sort(s3+1,s3+N+1,cmpS);
for(int i=1;i<=N;i++){
int Hmin=s1[i].H;
int p1=1,p2=1,cnt=0;
for(int j=1;j<=N;j++)Vis[j]=0;
for(int j=1;j<=N;j++){
int Vmin=s2[j].V;
for(;p1<=N&&s3[p1].S<=C+Hmin*A+Vmin*B;p1++)
if(s3[p1].H>=Hmin)cnt+=(Vis[s3[p1].id]==0),Vis[s3[p1].id]=1;
for(;p2<=N&&s2[p2].V<Vmin;p2++)
if(s2[p2].H>=Hmin)cnt-=Vis[s2[p2].id],Vis[s2[p2].id]=1;
Ans=max(Ans,cnt);
}
}
printf("%d
",Ans);
}
/*
H*A+V*B<=C+Hmin*A+Vmin*B
H>=Hmin V>=Vmin
*/