在普通的PID控制算法中,由于积分系数Ki是常数,所以在整个控制过程中,积分增量是不变的。然而,系统对于积分项的要求是,系统偏差大时,积分作用应该减弱甚至是全无,而在偏差小时,则应该加强。积分系数取大了会产生超调,甚至积分饱和,取小了又不能短时间内消除静差。因此,如何根据系统的偏差大小改变积分速度,对提高系统的品质是有必要的。变积分PID算法正好可以满足这一要求。
1、变积分的基本思想
变积分PID的基本思想是设法改变积分项的累加速度,使其与偏差大小相对应:偏差越大,积分越慢; 偏差越小,积分越快。设定系数为f(err(k)),它是err(k)的函数。当|err(k)|增大时,f减小,反之增大。变积分的PID积分项表达式为:
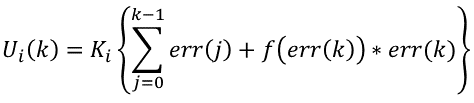
其中f(err(k))与|err(k)|的函数关系可根据具体情况设定,可以是线性的也可以是非线性的,通常比较简单的设置如下:
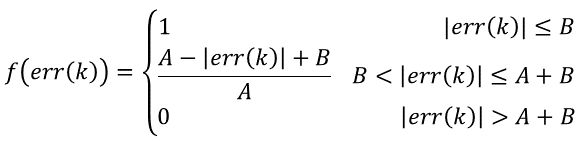
由以上公式可知,f(err(k))的值在[0,1]区间变化,当偏差值|err(k)|大于分离区间A+B时,不对当前偏差err(k)进行累加;当偏差值|err(k)|小于B时,加入当前偏差err(k)进行累加;介于B和A+B的区间时,按一定函数关系随err(k)变化。于是变积分PID算法可以表示为:
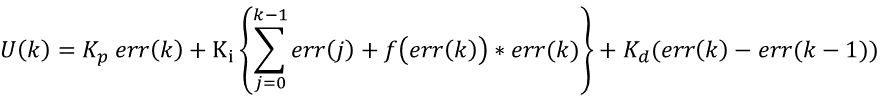
上述的f(err(k))函数只是我们列举的一种,事实上可以采取任何可行的方式,甚至是非线性函数,只要更符合控制对象的特性。
对于用增量型PID算法的变积分表示如下:
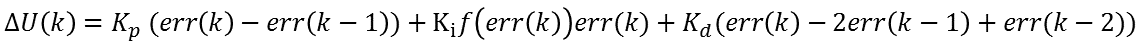
看到这个公式,很多人可能会发觉与前面的积分分离算法的公式很象。特别是在增量型算法中,它们的形式确实是一样的,但表达的意思确是有一定区别,那么我们来看看有什么不同呢?在后面我们再作总结。
2、算法实现
变积分实际上是通过对偏差的判断,让积分以不同的速度累计。这一系数介于0-1之间,可以通过多种方式实现,在这里我们按线性方式实现。变积分的控制流程图如下:
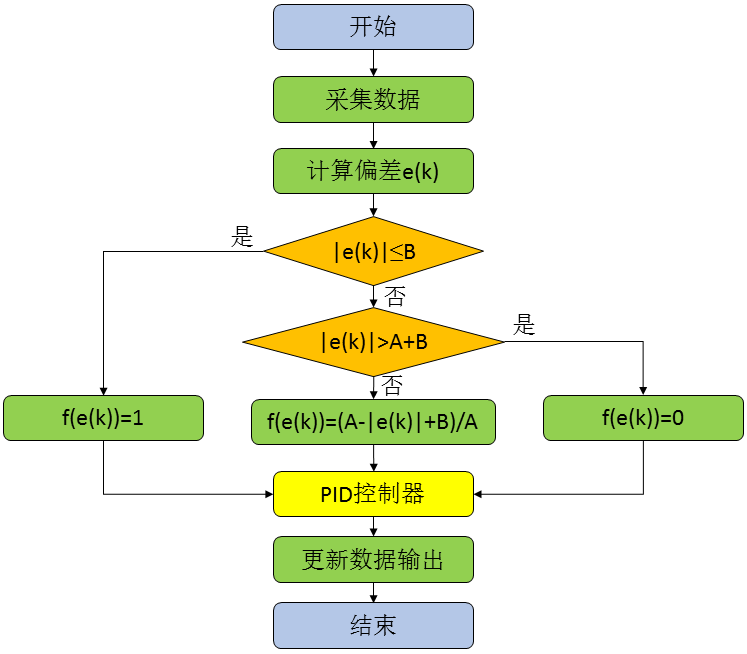
首先实现一个处理f(e(k))的函数,有前面的函数关系表达式,实现为响应的编码就很简单了:
1 /* 变积分系数处理函数,实现一个输出0和1之间的分段线性函数 */ 2 /* 当偏差的绝对值小于最小值时,输出为1;当偏差的绝对值大于最大值时,输出为0 */ 3 /* 当偏差的绝对值介于最大值和最小值之间时,输出在0和1之间现行变化 */ 4 /* float error,当前输入的偏差值 */ 5 /* float absmax,偏差绝对值的最大值 */ 6 /* float absmin,偏差绝对值的最小值 */ 7 static float VariableIntegralCoefficient(float error,float absmax,float absmin) 8 { 9 10 float factor=0.0; 11 12 if(abs(error)<=absmin) 13 { 14 15 factor=1.0; 16 17 } 18 else if(abs(error)>absmax) 19 { 20 21 factor=0.0; 22 23 } 24 else 25 26 { 27 28 factor=(absmax-abs(error))/(absmax-absmin); 29 30 } 31 32 return factor; 33 34 }
(1)位置型PID算法实现
变积分基于位置型PID的实现就是更具偏差绝对值的大小获取变积分的系数。然后再实现PID算法,同样首先定义PID对象的结构体:
1 /*定义结构体和公用体*/ 2 3 typedef struct 4 5 { 6 7 float setpoint; //设定值 8 9 float proportiongain; //比例系数 10 11 float integralgain; //积分系数 12 13 float derivativegain; //微分系数 14 15 float lasterror; //前一拍偏差 16 17 float result; //输出值 18 19 float integral;//积分值 20 21 float errorabsmax; //偏差绝对值最大值 22 23 float errorabsmin; //偏差绝对值最小值 24 25 }PID;
接下来实现PID控制器:
1 void PIDRegulation(PID *vPID, float processValue) 2 { 3 4 float thisError; 5 6 float factor; 7 8 thisError=vPID->setpoint-processValue; 9 10 factor= VariableIntegralCoefficient(thisError, vPID->errorabsmax, vPID->errorabsmin); 11 12 13 14 vPID->integral+= factor*thisError; 15 16 vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+vPID->derivativegain*(thisError-vPID->lasterror); 17 18 vPID->lasterror=thisError; 19 20 }
(2)增量型PID算法实现
同样变积分基于增量型PID的实现也是一样的。首先定义PID对象的结构体:
1 /*定义结构体和公用体*/ 2 typedef struct 3 { 4 5 float setpoint; //设定值 6 7 float proportiongain; //比例系数 8 9 float integralgain; //积分系数 10 11 float derivativegain; //微分系数 12 13 float lasterror; //前一拍偏差 14 15 float preerror; //前两拍偏差 16 17 float deadband; //死区 18 19 float result; //输出值 20 21 float errorabsmax; //偏差绝对值最大值 22 23 float errorabsmin; //偏差绝对值最小值 24 25 }PID;
接下来实现PID控制器:
1 void PIDRegulation(PID *vPID, float processValue) 2 { 3 4 float thisError; 5 6 float increment; 7 8 float pError,dError,iError; 9 10 float factor; 11 12 13 14 thisError=vPID->setpoint-processValue; //得到偏差值 15 16 factor= VariableIntegralCoefficient(thisError, vPID->errorabsmax, vPID->errorabsmin); 17 18 19 20 pError=thisError-vPID->lasterror; 21 22 iError= factor*thisError; 23 24 dError=thisError-2*(vPID->lasterror)+vPID->preerror; 25 26 increment=vPID->proportiongain*pError+vPID->integralgain*iError+vPID->derivativegain*dError; //增量计算 27 28 vPID->preerror=vPID->lasterror; //存放偏差用于下次运算 29 30 vPID->lasterror=thisError; 31 32 vPID->result+=increment; 33 34 }
3、总结
变积分实际上有一定的专家经验在里面,因为限值的选取以及采用什么样的函数计算系数,有很大的灵活性。
我们在前面做了积分分离的算法,这次又说了变积分的算法。他们有相通的地方,也有不同的地方,下面对他们进行一些说明。
首先这两种算法的设计思想是有区别的。积分分离的思想是偏差较大时,取消积分;而偏差较小时引入积分。变积分的实现是想是设法改变积分项的累加速度,偏差大时减弱积分;而偏差小时强化积分。有些所谓改进型的积分分离算法实际已经脱离了积分分离的基本思想,而是动态改变积分系数。就这一点而言,特别是在增量型算法中,已经属于变积分的思想了。
其次,对于积分分离来说,该操作是针对整个积分项操作,这一点在位置型PID算法中,表现的尤为明显。而对于变积分来说,是针对当前偏差的积分累计,就是说只影响当前这次的积分部分。再者,具体的实现方式也存在区别,特别是在位置型PID方式下尤为明显。
我们在这里讨论它们的区别原因,佷显然就是我们没办法同时采用这两种优化方式,只能分别实现,在后面我们将实现基于积分项的优化。
欢迎关注:
