Cat Noku has obtained a map of the night sky. On this map, he found a constellation with n stars numbered from 1to n. For each i, the i-th star is located at coordinates (xi, yi). No two stars are located at the same position.
In the evening Noku is going to take a look at the night sky. He would like to find three distinct stars and form a triangle. The triangle must have positive area. In addition, all other stars must lie strictly outside of this triangle. He is having trouble finding the answer and would like your help. Your job is to find the indices of three stars that would form a triangle that satisfies all the conditions.
It is guaranteed that there is no line such that all stars lie on that line. It can be proven that if the previous condition is satisfied, there exists a solution to this problem.
The first line of the input contains a single integer n (3 ≤ n ≤ 100 000).
Each of the next n lines contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109).
It is guaranteed that no two stars lie at the same point, and there does not exist a line such that all stars lie on that line.
Print three distinct integers on a single line — the indices of the three points that form a triangle that satisfies the conditions stated in the problem.
If there are multiple possible answers, you may print any of them.
3
0 1
1 0
1 1
1 2 3
5
0 0
0 2
2 0
2 2
1 1
1 3 5
In the first sample, we can print the three indices in any order.
In the second sample, we have the following picture.
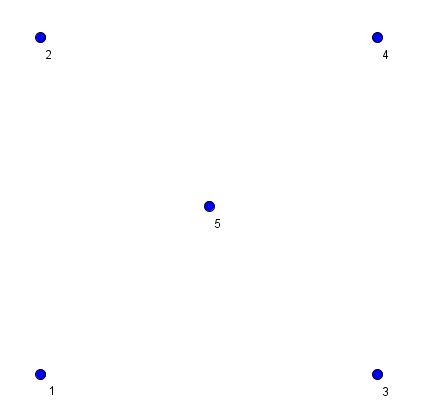
Note that the triangle formed by starts 1, 4 and 3 doesn't satisfy the conditions stated in the problem, as point 5 is not strictly outside of this triangle (it lies on it's border).
题意
给出n个点的坐标,找出任意三个点符合组成的三角形内不包含别的点
分析
我最先想的是选定第一个点,然后求别的点到它的距离,然后选离最近的点和第二近的点,共线的话去看第三近....但是这样WA了,为什么呢,待解释。。
解释来了,原来是我共线的判断方法写错了,改了一下也可以AC。详情看补充的代码↓。
正确的做法是把所有点按照xy坐标排序,先排x,x相同考虑y。
然后选取第一个点第二个点,然后第三个点看看是否共线,是则看第四个点...
判断是否共线就是斜率相同,(y1-y2)/(x1-x2)==(y3-y2)/(x3-x2)那就是(y1-y2)*(x3-x2)==(x1-x2)*(y3-y2)
代码
#include <stdio.h> #include <algorithm> #define F(a,b,c) for(int a=b;a<=c;a++) #define N 100005 #define ll long long using namespace std; ll n,m=3; struct num{ll x,y,id;}a[N]; int cmp(num a,num b){return a.x<b.x||a.x==b.x&&a.y<b.y;} int main() { scanf("%lld",&n); F(i,1,n) scanf("%lld%lld",&a[i].x,&a[i].y),a[i].id=i; sort(a+1,a+n+1,cmp); while((a[1].x-a[2].x)*(a[1].y-a[m].y)==(a[1].y-a[2].y)*(a[1].x-a[m].x))m++; printf("%lld %lld %lld",a[1].id,a[2].id,a[m].id); return 0; }
补充的代码
#include <stdio.h> #include <algorithm> #define F(a,b,c) for(int a=b;a<=c;a++) #define N 100005 #define ll long long using namespace std; ll n,x[N],y[N],a=3; struct num { double v; ll x,y,id; } d[N]; int cmp(num a,num b) { return a.v<b.v; } ll jl(ll a,ll b) { return (d[a].x-d[b].x)*(d[a].x-d[b].x)+(d[a].y-d[b].y)*(d[a].y-d[b].y); } int main() { scanf("%I64d",&n); F(i,1,n) { scanf("%I64d%I64d",&d[i].x,&d[i].y); if(i>1) d[i].v=jl(i,1),d[i].id=i; } sort(d+2,d+n+1,cmp); while((d[1].y-d[a].y)*(d[1].x-d[2].x)==(d[1].x-d[a].x)*(d[1].y-d[2].y)&&a<n)a++; printf("1 %I64d %I64d",d[2].id,d[a].id); return 0; }