题目描述
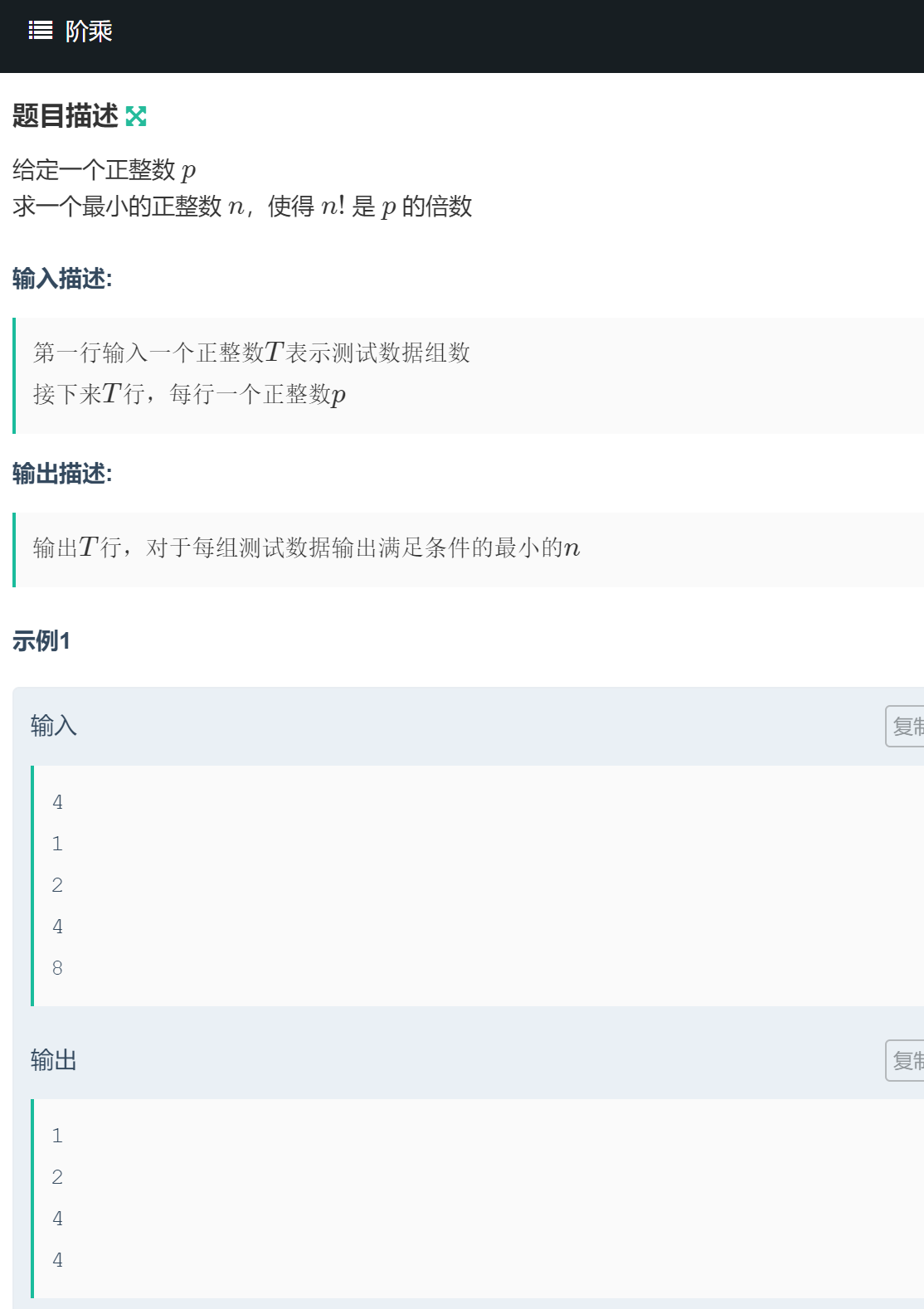
题目地址:https://ac.nowcoder.com/acm/contest/4784/B
思路
1.对p质因数分解,根据唯一分解定理,可以分解出唯一的如下表达式
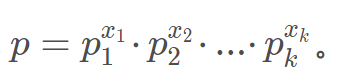
2.对n!进行质因数分解的话,也可以分解出p1x1,p2x2,p3^x3....,求n!中因子p的个数,参考这道题
3.如果n!中对应的质因子的次数x1,x2,x3...都大于p中因子幂次,那么n!就是p的倍数。
4.二分答案n即可
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t;
ll p;
vector<pair<int,int> > v;
bool check(ll n){
for(int i=0;i<v.size();i++){
ll cnt = 0, temp = n;
//分解n!的因子
while(temp){
cnt += temp/v[i].first;
temp /= v[i].first;
}
//如果n!的因子v[i]的个数 比p的少,那么n!肯定就不是p的倍数了
if(cnt < v[i].second) return false;
}
return true;
}
void solve(){
v.clear();
cin>>p;
ll l = 1,r = p,mid,ans = 1;
//p进行质因子分解, x^a y^b z^c...
for(int i=2;i*i<=p;i++){
if(p%i == 0){
int cnt = 0;
while(p%i == 0){
p /= i;
cnt++;
}
v.push_back({i,cnt});
}
}
if(p > 1) v.push_back({p,1});
//二分搜索答案 n
while(l <= r){
mid = (l+r) >> 1;
if(check(mid) == true) {
r = mid - 1;
}else{
l = mid + 1;
ans = l;
}
}
cout<<l<<endl;
}
int main(){
cin>>t;
while(t--){
solve();
}
return 0;
}