01 Trie 专题
异或最大值
The xor largest pair
题意： 异或最大值的模板。一个数和一个序列中一个数的异或最大值是多少？要支持询问。
思路:考虑把序列插入，构建一个 ( ext{Trie}) 树。那么在询问时，只需要讨论该数的位是 (0) 还是 (1) 就行了。这样就需要 (O(nlog w)) 的预处理，(O(log w)) 的询问和修改，为什么是对的。因为异或中我们如果可以满足最高位，那么没有理由不改变最高位，因为 (2^{bit} >sum_{i=0}^{i < bit}2^i) 。那么由高位到地位贪心就可以了。
/*
https://ac.nowcoder.com/acm/problem/50993
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e6 + 100;
int ch[maxn][2];
int sz = 0, rt, n;
int read() {int x; scanf("%d", &x); return x;}
void insert(int u, int t, int x){
if(t < 0) return;
int f = ((x >> t) & 1);
if(!ch[u][f]) ch[u][f] = ++sz;
insert(ch[u][f], t-1, x);
}
int ask(int u, int t, int x){
if(t < 0) return 0;
int f = ((x >> t) & 1);
if(ch[u][!f]) return ask(ch[u][!f], t-1, x) + (1 << t);
return ask(ch[u][f], t-1, x);
}
int main(){
n = read();
int ans = 0;
rt = ++ sz;
for(int i = 0; i < n; i++){
int x = read();
insert(rt, 30, x);
if(i != 0) ans = max(ans, ask(rt, 30, x));
}
printf("%d
", ans);
return 0;
}
Xor Sum
Problem Description
Zeus 和 Prometheus 做了一个游戏，Prometheus 给 Zeus 一个集合，集合中包含了N个正整数，随后 Prometheus 将向 Zeus 发起M次询问，每次询问中包含一个正整数 S ，之后 Zeus 需要在集合当中找出一个正整数 K ，使得 K 与 S 的异或结果最大。Prometheus 为了让 Zeus 看到人类的伟大，随即同意 Zeus 可以向人类求助。你能证明人类的智慧么？
Input
输入包含若干组测试数据，每组测试数据包含若干行。
输入的第一行是一个整数(T（T < 10）)，表示共有T组数据。
每组数据的第一行输入两个正整数(N，M（<1=N,M<=100000）)，接下来一行，包含N个正整数，代表 Zeus 的获得的集合，之后M行，每行一个正整数S，代表 Prometheus 询问的正整数。所有正整数均不超过(2^{32})。
Output
对于每组数据，首先需要输出单独一行”Case #?:”，其中问号处应填入当前的数据组数，组数从1开始计算。
对于每个询问，输出一个正整数K，使得K与S异或值最大。
Sample Input
2
3 2
3 4 5
1 5
4 1
4 6 5 6
3
Sample Output
Case #1:
4
3
Case #2:
4
同上题，简单板子
代码
/*
http://acm.hdu.edu.cn/showproblem.php?pid=4825
*/
#include<bits/stdc++.h>
using namespace std;
int read(){int x; scanf("%d", &x); return x;}
const int maxn = 5e6 + 10;
int ch[maxn][2], value[maxn];
int a[maxn];
int sz = 1, rt = 1;
int m, n, t, T;
void insert(int u, int t, int x){
if(t < 0) { value[u] = x; return; }
int i = (x >> t) & 1;
if(!ch[u][i]) ch[u][i] = ++sz;
insert(ch[u][i], t - 1, x);
}
int query(int u, int t, int x){
if(t < 0) return value[u];
int i = (x >> t) & 1;
if(ch[u][!i]) return query(ch[u][!i], t-1, x);
return query(ch[u][i], t - 1, x);
}
void solve(){
n = read(); m = read();
memset(ch, 0, sizeof ch);
sz = rt = 1;
memset(value, 0, sizeof value);
for(int i = 1; i <= n; i++) a[i] = read(), insert(rt, 31, a[i]);
printf("Case #%d:
", t - 1);
for (int i = 1; i <= m; i++){
int s = read();
printf("%d
", query(rt, 31, s));
}
}
int main(){
t = 1; T = read();
while(t++ <= T) solve();
return 0;
}
异或最小值
Vitya and Strange Lesson
((a_1,a_2,a_3..a_n) oplus Aoplus B) 根据结合率，等价于 ((a_1,a_2,a_3..a_n) oplus (Aoplus B)) 。
因为我们要求的是 (mex) ，那么我们就考虑 (0) 到 (mex-1) 的数是否全部出现过。那么就变为查询异或最小值了，我们在构建 ( ext{01 Trie}) 时要顺便记录 ( ext{Trie}) 中的元素个数，也就是(sz)，当一个节点的元素个数填满时，我们是不能考虑的。
/*
https://ac.nowcoder.com/acm/problem/112209
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn = 6e6 + 10;
int read(){ int x; scanf("%d", &x); return x;}
int sz[maxn], ch[maxn][2];
int size = 1, rt = 1;
int n, m, last;
void insert(int u, int t, int x){
if(t < 0){sz[u] = 1; return;}
int i = (x >> t) & 1;
if(!ch[u][i]) ch[u][i] = ++size;
insert(ch[u][i], t - 1, x);
sz[u] = sz[ch[u][i]] + sz[ch[u][!i]];
}
int query(int u, int t, int x){
if(t < 0 || u == 0) return 0;
int i = (x >> t) & 1;
if((1 << t) != sz[ch[u][i]]) return query(ch[u][i], t - 1, x);
else return query(ch[u][!i], t - 1, x) + (1 << t);
}
int main(){
n = read(); m = read();
for(int i = 1; i <= n; i++) insert(rt, 20, read());
while(m--){
last ^= read();
printf("%d
", query(rt, 20, last));
}
return 0;
}
保存值的异或最大值
奶牛异或
(aoplus a = 0) ，我们可以考虑做一次前缀异或和。那么区间操作就变为单点操作了。
/*
https://ac.nowcoder.com/acm/problem/22998
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e7 + 100;
int ch[maxn][2], id[maxn], a[maxn];
int sz = 0, rt, n;
int ans1, ans2 = 1, ans3 = 1;
int read() {int x; scanf("%d", &x); return x;}
void insert(int u, int t, int x, int ID){
if(t < 0){ id[u] = ID; return; }
int f = ((x >> t) & 1);
if(!ch[u][f]) ch[u][f] = ++sz;
insert(ch[u][f], t-1, x, ID);
}
int ask(int u, int t, int x){
if(t < 0) return id[u];
int f = ((x >> t) & 1);
if(ch[u][!f]) return ask(ch[u][!f], t-1, x);
return ask(ch[u][f], t-1, x);
}
int main(){
n = read(); a[0] = 0;
for(int i = 1; i <= n; i++) (a[i] = a[i-1] ^ read());
rt = ++ sz;
for(int i = 1; i <= n; i++){
insert(rt, 22, a[i-1], i);
int x = ask(rt, 22, a[i]) - 1;
if(ans1 < (a[x] ^ a[i])){
ans1 = (a[x] ^ a[i]);
ans2 = x + 1;
ans3 = i;
}
}
printf("%d %d %d
", ans1, ans2, ans3);
return 0;
}
带删除的异或最小值
我们在( ext{01 Trie}) 上再维护一个(sz_i) 标记，表示是否这个节点下还有没有可用元素。那么删除和插入都只会影响一条链。
/*
https://ac.nowcoder.com/acm/problem/112567
*/
#include<bits/stdc++.h>
using namespace std;
int read(){int x; scanf("%d", &x); return x;}
const int maxn = 6e6 + 10;
int ch[maxn][2], sz[maxn];
int size = 0, rt = 0;
int n, m;
int a[maxn], b[maxn], c[maxn];
void insert(int u, int t, int x){
if(t < 0) return;
int i = (x >> t) & 1;
if(!ch[u][i]) ch[u][i] = ++size;;
sz[ch[u][i]]++;
insert(ch[u][i], t - 1, x);
}
void erase(int u, int t, int x){
if(t < 0) return;
int i = (x >> t) & 1;
sz[ch[u][i]]--;
erase(ch[u][i], t - 1, x);
}
int query(int u, int t, int x){
if(t < 0) return 0;
int i = (x >> t) & 1;
if(sz[ch[u][i]]) return query(ch[u][i], t-1, x) + (i << t);
else return query(ch[u][!i], t-1, x) + ((!i) << t);
}
int main(){
n = read();
for(int i = 1; i <= n; i++) a[i] = read();
for(int i = 1; i <= n; i++) b[i] = read(), insert(rt, 30, b[i]);
for(int i = 1; i <= n; i++){
int x = query(rt, 30, a[i]);
printf("%d
", a[i] ^ x);
erase(rt, 30, x);
}
return 0;
}
带删除的异或最大值
D. Vasiliy's Multiset
Author has gone out of the stories about Vasiliy, so here is just a formal task description.
You are given q queries and a multiset A, initially containing only integer 0. There are three types of queries:
- "+ x" — add integer x to multiset A.
- "- x" — erase one occurrence of integer x from multiset A. It's guaranteed that at least one x is present in the multiset A before this query.
- "? x" — you are given integer x and need to compute the value
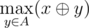, i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer x and some integer y from the multiset A.
Multiset is a set, where equal elements are allowed.
Input
The first line of the input contains a single integer$q (1 ≤ q≤ 200 000) $— the number of queries Vasiliy has to perform.
Each of the following q lines of the input contains one of three characters '+', '-' or '?' and an integer (x_i (1 ≤ x_i ≤ 10^9)). It's guaranteed that there is at least one query of the third type.
Note, that the integer 0 will always be present in the set A.
Output
For each query of the type '?' print one integer — the maximum value of bitwise exclusive OR (XOR) of integer x**i and some integer from the multiset A.
input
10
+ 8
+ 9
+ 11
+ 6
+ 1
? 3
- 8
? 3
? 8
? 11
output
11
10
14
13
Note
After first five operations multiset A contains integers (0, 8, 9, 11, 6 and 1.)
The answer for the sixth query is integer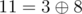 
— maximum among integers 
, 
, 
, 
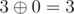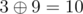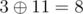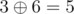and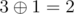 
.
题意
初始有个一个空集，n个操作，操作分三种
- ＋x，将一个 x 加入集合
- －x，删除集合内的一个 x
- ？x，询问集合中与 x 异或的最大值
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 6e6 + 10;
int ch[maxn][2], sz[maxn], val[maxn], cnt[maxn];
int size = 0, rt = 0;
int n, m;
void insert(int u, int t, int x){
if(t < 0) { val[u] = x; return;}
int i = (x >> t) & 1;
if(!ch[u][i]) ch[u][i] = ++size;
sz[ch[u][i]]++;
insert(ch[u][i], t - 1, x);
}
void erase(int u, int t, int x){
if(t < 0) return;
int i = (x >> t) & 1;
sz[ch[u][i]]--;
erase(ch[u][i], t - 1, x);
}
int query(int u, int t, int x){
if(t < 0) return val[u];
int i = (x >> t) & 1;
if(sz[ch[u][!i]]) return query(ch[u][!i], t-1, x);
else return query(ch[u][i], t-1, x);
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
char c; cin >> c;
int t; cin >> t;
if(c == '+') insert(rt, 30, t);
else if(c == '-') erase(rt, 30, t);
else printf("%d
", max(t, query(rt, 30, t) ^ t));
}
return 0;
}
/*
12
? 1
+ 1
+ 4
? 5
? 6
*/