基于贝叶斯理论的有监督学习算法
“朴素”：
因为这个算法是 基于样本特征之间相互独立的“朴素”假设
正因为如此，由于不考虑样本之间特征的关系——> 朴素贝叶斯分类器效率极高
朴素贝叶斯基本概念
1.贝叶斯定理
详细：https://www.jianshu.com/p/7e8504e9b929
2.简单应用
用1表示下雨，0表示不下雨：
过去的7天可以表示为： y = [0,1,1,0,1,0,0]
和气象有关的别的信息，如刮北风，闷热，多云，天气预保是否有雨——> 用1表示是，0表示否
则可得：X = [0,1,0,1],[1,1,1,0],[0,1,1,0],[0,0,0,1],[0,1,1,0],[0,1,0,1],[1,0,0,1]
数据关系：
#导入numpy
import numpy as np
#讲X，y赋值为np数组
X = np.array([[0,1,0,1],
[1,1,1,0],
[0,1,1,0],
[0,0,0,1],
[0,1,1,0],
[0,1,0,1],
[1,0,0,1]])
y = np.array([0,1,1,0,1,0,0])
#对不同分类计算每个特征为1的数量
counts = {}
for label in np.unique(y):
counts [label] = X[y == label].sum(axis=0)
#打印计数结果
print("feature counts:{}".format(counts))
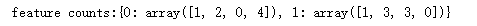
【结果分析：】
y = 0即无雨的4天中，1天刮北风，2天闷热，0天多云，4天天气预保有雨
y = 1即有雨的3天中，1天刮北风，3天闷热，3天多云，0天天气预保有雨
对于朴素贝叶斯来说，会根据上述的计算来推理，它会认为，如果天气预保没雨，但出现了多云，会倾向于把这一天放到“下雨”分类中
#导入贝努利贝叶斯
from sklearn.naive_bayes import BernoulliNB
#使用贝努利贝叶斯拟合数据
clf = BernoulliNB()
clf.fit(X,y)
#要预测的这一天，没有北风，也不闷热，但多云，天气预报没说下雨
Next_Day = [[0,0,1,0]]
pre = clf.predict(Next_Day)
#结果
if pre == [1]:
print ("下雨")
else:
print ("晴天")
下雨
如果另外一天，刮北风，闷热，不多云，预保有雨会怎样？
#假设另一天的数据如下
Another_day = [[1,1,0,1]]
#使用训练好的模型预测
pre2 = clf.predict(Another_day)
#结果
if pre2 ==[1]:
print("下雨")
else:
print("晴天")
晴天
准确率？
print(clf.predict_proba(Next_Day))
#第二天准确率
print(clf.predict_proba(Another_day))
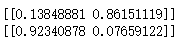【第一个是不下雨的概率，第二个是下雨的概率】
# 朴素贝叶斯是相当好的分类器，但对于预测具体的数值并不是很擅长，所以predict_proba给出的预测概率，不要太当真
朴素贝叶斯的不同方法
在sklearn中，朴素贝叶斯有三种方法：贝努利朴素贝叶斯、高斯朴素贝叶斯、多项式朴素贝叶斯
贝努利朴素贝叶斯
适合符合贝努利分布【二项分布】的数据集
刚才的例子，数据集中的每个特征只有0 1 两个数值，贝努利表现不错，下方使用更复杂的数据集：
#导入数据集生成工具
from sklearn.datasets import make_blobs
#导入数据集拆分工具
from sklearn.model_selection import train_test_split
#生成样本数据量为500，分类数为5的数据集
X,y = make_blobs(n_samples=500,centers=5,random_state=8)
#将数据集拆分为训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=8)
#使用贝努力贝叶斯拟合数据
nb = BernoulliNB()
nb.fit(X_train,y_train)
#结果
print(nb.score(X_test,y_test))
0.544
得分很差，只有一半的数据被放进了正确的分类中
用图像了解贝努利朴素贝叶斯的工作过程：
#导入画图工具
import matplotlib.pyplot as plt
#限定横纵轴的最大值
x_min,x_max = X[:,0].min() -0.5,X[:,0].max() +0.5
y_min,y_max = X[:,1].min() -0.5,X[:,1].max() +0.5
#用不同的背景色表示不同的分类
xx,yy = np.meshgrid(np.arange(x_min,x_max,.02),
np.arange(y_min,y_max,.02))
z = nb.predict(np.c_[(xx.ravel(),yy.ravel())]).reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Pastel1)
#将训练集和测试集的结果用散点图表示
plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k')
plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,marker='*',edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
#定义图题
plt.title("Classifier:BernoulliNB")
plt.show()
【结果分析】：模型非常简单，在横轴=0和纵轴=0的位置画两条直线，再用这两条直线形成的四个象限对数据分类
这是因为使用了默认的参数 bnarize = 0.0 所以，模型对于数据的判断就是 如果特征1 > /=0，且特征2 >/=0,分为1类；如果特征1 < 0且特征2 <0,分为另一类；其余的都分为一类
高斯朴素贝叶斯
适用：样本的特征符合高斯分布【正态分布】
对上方实例采用高斯朴素贝叶斯算法：
#导入高斯朴素贝叶斯
from sklearn.naive_bayes import GaussianNB
#使用高斯朴素贝叶斯拟合数据
gnb = GaussianNB()
gnb.fit(X_train,y_train)
#结果
print(gnb.score(X_test,y_test))
0.968
用图像演示以了解工作过程：
#用不同的色块表示不同的分类
z = gnb.predict(np.c_[(xx.ravel(),yy.ravel())]).reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Pastel1)
#用散点图画出训练集和测试集的数据
plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k')
plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,marker='*',edgecolor='k')
#设置横纵轴范围
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
#定义图题
plt.title("Classifier:GaussianNB")
plt.show()
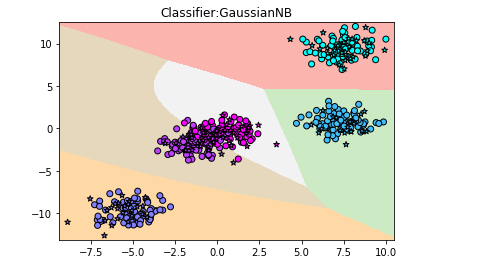
【结果分析】：分类边界更复杂，基本把数据点都放进了正确的分类中
多项式朴素贝叶斯
用于拟合多项式分布的数据集
二项式分布——> 抛硬币【结果只有2个，正反】
多项式分布——> 掷骰子【6个面，有6个结果，如果掷n次，而每个面朝上的次数的分布情况就是一个多项式分布】
继续用上上方的数据集实验：
#导入多项式朴素贝叶斯
from sklearn.naive_bayes import MultinomialNB
#拟合数据
mnb = MultinomialNB()
mnb.fit(X_train,y_train)
mnb.score(X_test,y_test)
会报错！！！
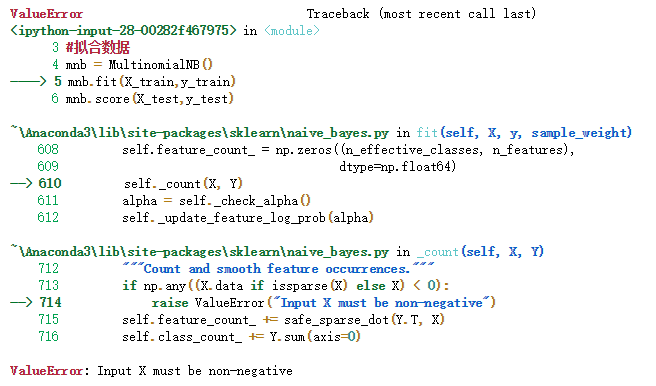
输入的X值必须非负！
对数据预处理：
#导入多项式朴素贝叶斯
from sklearn.naive_bayes import MultinomialNB
#导入数据预处理工具MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
#使用MinMaxScaler对数据预处理，使数据全部非负
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
#拟合
mnb = MultinomialNB()
mnb.fit(X_train_scaled,y_train)
#结果
print(mnb.score(X_test_scaled,y_test))
0.32
用图形表示的话，可以看出多项式朴素贝叶斯不适用此数据集：
#用不同的色块表示不同的分类
z = mnb.predict(np.c_[(xx.ravel(),yy.ravel())]).reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Pastel1)
#用散点图画出训练集和测试集的数据
plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k')
plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,marker='*',edgecolor='k')
#设置横纵轴范围
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
#定义图题
plt.title("Classifier:MultinomialNB")
plt.show()
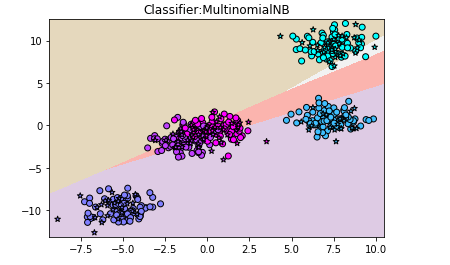
【结果分析】：多项式朴素贝叶斯只适合用来对非负离散数值特征进行分类
典例就是，对转化为向量后的文本数据进行分类
#本例中，用MinMaxScaler 对数据预处理，其作用是将数据集中的特征值转化为 0~1
实战——判断肿瘤良性还是恶性
1. 此数据集包含569个病例的数据样本，每个样本有30个特征值，样本共分为2类：恶性 良性
#导入肿瘤数据集
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
#打印数据集键值
print(cancer.keys())
#打印分类
print(cancer['target_names'])
#打印特征名称
print(cancer['feature_names'])
2. 分析，这个数据集的特征并不属于二项分布，也不属于多项式分布，所以选择高斯朴素贝叶斯建模
首先，将数据集拆分为训练集和测试集：
#将数据集的数值和分类目标复制给x y
X, y = cancer.data,cancer.target
#使用数据集拆分工具
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=8)
#打印训练集和测试集的数据形态
print(X_train.shape)
print(X_test.shape)
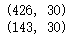
其次，拟合训练集：
#使用高斯朴素贝叶斯拟合
gnb = GaussianNB()
gnb.fit(X_train,y_train)
#打印评分
print(gnb.score(X_train,y_train))
print(gnb.score(X_test,y_test))
随机用样本让模型预测：如第312个样本
#预测分类
print(gnb.predict([X[312]]))
#正确分类
print(y[312])
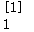
高斯朴素贝叶斯的学习曲线：
学习曲线：
指随着数据集样本数量的增加，模型得分变化情况
#导入学习曲线库
from sklearn.model_selection import learning_curve
#导入随机拆分工具
from sklearn.model_selection import ShuffleSplit
#定义一个函数绘制学习曲线
def plot_learning_curve(estimator,title,X,y,ylim=None,cv=None,n_jobs=1,train_sizes=np.linspace(.1,1.0,5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
#设置横轴标签
plt.xlabel("Training examples")
#设置纵轴标签
plt.ylabel("Score")
train_sizes,train_scores,test_scores = learning_curve(estimator,X,y,cv=cv,n_jobs=n_jobs,train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores,axis=1)
test_scores_mean = np.mean(test_scores,axis=1)
plt.grid()
plt.plot(train_sizes,train_scores_mean,'o-',color='r',label="Training score")
plt.plot(train_sizes,test_scores_mean,'o-',color='g',label="Croass-validation score")
plt.legend(loc="Lower right")
return plt
#设置图题
title = "Learning Curves (Naive Bayes)"
#设定拆分数量
cv = ShuffleSplit(n_splits=100,test_size=0.2,random_state=0)
#设定模型为高斯朴素贝叶斯
estimator = GaussianNB()
#调用定义好的函数
plot_learning_curve(estimator,title,X,y,ylim=(0.9,1.01),cv=cv,n_jobs=4)
plt.show()
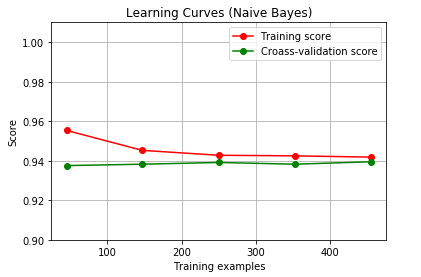
【结果分析】：模型交叉验证得分变化不怎么明显-—>高斯朴素贝叶斯在预测方面，对于样本数量的要求不苛刻
- 高斯朴素贝叶斯 可以应用于任何连续数值型的数据集中，如果是符合正态分布的数据集的话，得分会更高
- 相对于线性模型，朴素贝叶斯效率更高——> 把数据集中的各个特征看作完全独立的，不考虑特征之间的关联关系，但同时，泛化能力更弱
- 大数据时代，很多数据集的样本特征成千上万，这种情况下，模型的效率要比泛化性能多零点几个百分点的得分更重要