一、用户态、内核态和中断
1、一般现代cpu都有几种不用的指令执行级别
2、在高执行级别下,代码可以执行特权指令,访问任意的物理地址,这种CPU执行级别就对应着内核态。
3、在相应的低级别执行状态下,代码的掌控范围会受到限制。只能对应级别允许的范围内活动。
例:intel x86CPU有四种不同的执行级别0-3,Linux只使用了其中的0级和3级分别表示内核态和用户态。
4、为什么需要权限级别的划分?
程序员写的代码可能健壮性不够,使得整个系统崩溃等问题。所以由更专业的程序猿写系统的执行代码,即使用内核态进行操作,保证它的健壮性。
5、对用户态和内核态明显区分的是cs和eip
cs寄存器的最低两位表明了当前代码的特权级。
CPU每条指令的读取都是通过cs:eip这两个寄存器:
其中cs是代码段选择寄存器,eip是偏移量寄存器。
上述判断由硬件完成。
一般来说在Linux中,地址空间是一个显著的标志:0xc0000000以上的地址空间只能在内核态下访问,0x0000000-0xbffffff的地址空间在两种状态下都可以访问。
这里的地址空间是指逻辑地址
6.中断处理是从用户态进入内核态的主要方式,系统调用只是一种特殊的中断。
(1)寄存器上下文:
从用户态切换到内核态时:①必须保存用户态的寄存器上下文②将内核态响应值放入对应的寄存器中
中断/int指令会在堆栈上保存一些寄存器的值,如:用户态栈顶地址、当时的状态字,当时的cs:eip的值。
中断发生后的第一件事就是保存现场保存现场就是进入中断程序,保存需要用到的寄存器的数据,中断发生后最后一件事是恢复现场,恢复现场就是退出中断程序,恢复保存寄存器的数据。
二、系统调用概述
1、操作系统为用户态进程与硬件设备进行交互提供了一组接口-------系统调用
把用户从底层的硬件编程中解放出来
极大提高了系统的安全性
是用户程序具有可移植性
2、应用编程接口(API)和系统调用不同
API只是一个函数定义(可以将一个系统调用封装为一个函数)
系统调用通过软中断向内核发出一个明确的请求
Libc库定义的一些API应用了封装例程(唯一目的就是发布系统调用,程序猿写代码时不需要用汇编指令)
一般每个系统调用对应一个封装例程,库再用这些封装例程定义出给用户的API
不是每一个API都对应一个特定的系统调用。
API可能直接提供用户态的服务。一个单独的API可能调用几个系统调用,不同的API可能调用了同一个系统调用。
3、返回值
大部分封装例程返回一个整数,其值的含义依赖于相应的系统调用。
-1在多数情况下表示内核不能满足进程的请求,Libc中定义的errno变量包含特定的出错码。
4、当用户态进程调用一个系统调用时,CPU切换到内核态并开始执行一个内核函数。
传参内核实现了很多不同的系统调用,进程必须指明需要哪个系统调用,这需要传递一个名为系统调用号的参数,使用eax寄存器传递。
5、系统调用也需要输入输出参数,例如
实际的值。
用户态进程地址空间的变量地址。
甚至是包含指向用户态函数的指针的数据结构地址。
寄存器传参限制:
(1)每个参数的长度不能超过寄存器的长度,即32位。
(2)在系统调用号(eax)之外,参数的个数不能超过6个(ebx,ecx,edx,esi,sdi,ebp)超过6个之后就会把某一个寄存器指向一块内存,可以访问所有内存。
三、使用库函数API获取系统当前时间

在进行本次实验时,遇到了很多问题,首先是编译为32位时,提示错误:

经过查询,是因为虚拟机的机器位数是64位,但是要编译为32位,所以需要使用命令:
sudo apt-get install libc6-dev-i386
但是在执行该条命令时,出现错误:链接不上软件源:

此时,设置DNS
sudo vim /etc/resolv.conf
将文件内容改为:

然后,重启网络服务,并更新apt
sudo apt-get update
然后正常安装
sudo apt-get install libc6-dev-i386
编译之后出现问题:
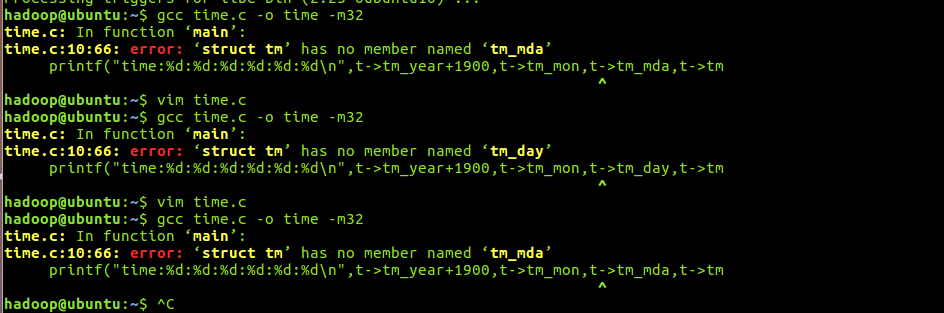
经过百度,发现,在tm结构体中的关于日的成员变量为tm_mday
改正之后,