POJ-3686 The Windy's KM算法 拆点题

参考：https://blog.csdn.net/sr_19930829/article/details/40680053

题意：

　　有n个订单，m个工厂，第i个订单在第j个工厂生产的时间为t[i][j],同一个工厂可以生产多个订单，但一次只能生产一个订单，也就是说如果先生产a订单，那么b订单要等到a生产完以后再生产，问n个订单用这m个工厂全部生产完需要最少的时间是多少。

思路：

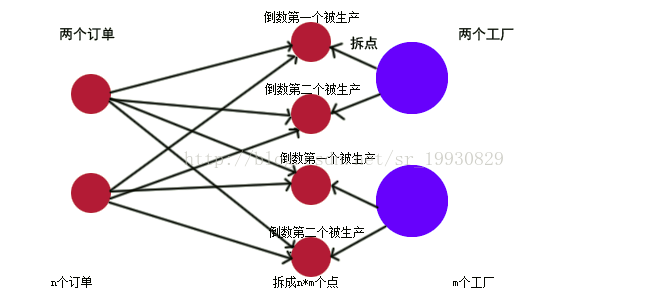
　　这道题好像用费用流也可以，建图思路好像也是一样的。每个订单耗费时间和在工厂中的等待顺序是有关系的。显然，如果一个工厂有k个订单，那么第一个商品 t1时间，第二个商品就是（t1 + t2）时间，第三个商品就是（t1+t2+t3)...因为我们考虑的是总时间，加起来 = t1 + (t1 + t2) + (t1 + t2 + t3) ... (t1 + t2 ... tk) 。去括号可以发现 K*t1 + (K-1) * t2 + ...tk。但这里你可能还像我一样不知所措。t1 贡献了 K 倍，t2 贡献了（K-1）倍，tk贡献了一倍。说得更清楚一些，某个工厂的倒数第 i 个订单贡献 i * t 的时间。所以我们要给每个工厂开n个点，这个点表示左边某个物品在第（1~n）个时的贡献。就是拆点的思想，每个工厂拆出n种情况。

图片可能更好理解（复制自参考）

#include <algorithm>
#include  <iterator>
#include  <iostream>
#include   <cstring>
#include   <iomanip>
#include   <cstdlib>
#include    <cstdio>
#include    <string>
#include    <vector>
#include    <bitset>
#include    <cctype>
#include     <queue>
#include     <cmath>
#include      <list>
#include       <map>
#include       <set>
//#include <unordered_map>
//#include <unordered_set>
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
using namespace std;
//#pragma GCC optimize(3)
//#pragma comment(linker, "/STACK:102400000,102400000")  //c++
#define lson (l , mid , rt << 1)
#define rson (mid + 1 , r , rt << 1 | 1)
#define debug(x) cerr << #x << " = " << x << "
";
#define pb push_back
#define pq priority_queue



typedef long long ll;
typedef unsigned long long ull;

typedef pair<ll ,ll > pll;
typedef pair<int ,int > pii;
typedef pair<int ,pii> p3;
//priority_queue<int> q;//这是一个大根堆q
//priority_queue<int,vector<int>,greater<int> >q;//这是一个小根堆q
//__gnu_pbds::cc_hash_table<int,int>ret[11];    //这是很快的hash_map
#define fi first
#define se second
//#define endl '
'

#define OKC ios::sync_with_stdio(false);cin.tie(0)
#define FT(A,B,C) for(int A=B;A <= C;++A)  //用来压行
#define REP(i , j , k)  for(int i = j ; i <  k ; ++i)
//priority_queue<int ,vector<int>, greater<int> >que;

const ll mos = 0x7FFFFFFFLL;  //2147483647
const ll nmos = 0x80000000LL;  //-2147483648
const int inf = 0x3f3f3f3f;
const ll inff = 0x3f3f3f3f3f3f3f3fLL; //18

const double PI=acos(-1.0);

template<typename T>
inline T read(T&x){
    x=0;int f=0;char ch=getchar();
    while (ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
    while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x=f?-x:x;
}

/*-----------------------showtime----------------------*/
            const int maxn = 100;
            int t[maxn][maxn];
            int mp[maxn][maxn*maxn];
            int visx[maxn],visy[maxn*maxn];
            int xn,xm,minz;
            int linkx[maxn],linky[maxn*maxn];
            int wx[maxn],wy[maxn * maxn];

            bool dfs(int x){
                visx[x] = true;
                for(int i=1; i<=xm; i++){
                    if(!visy[i]){
                        int t = wx[x] + wy[i] - mp[x][i];

                        if(t==0){
                            visy[i] = true;
                            if(!linky[i] || dfs(linky[i])){
                                linky[i] = x;
                                linkx[x] = i;
                                return true;
                            }
                        }
                        else if(t>0)minz = min(minz, t);
                    }
                }   
                return false;
            }
            int km(){
                for(int i=1; i<=max(xn,xm); i++)
                    linkx[i] = linky[i] = 0;
                for(int i=1; i<=xm; i++)wy[i] = 0;
                for(int i=1; i<=xn; i++){
                    wx[i] = -inf;
                    for(int j=1; j<=xm; j++){
                        wx[i] = max(wx[i], mp[i][j]);
                    }
                }

                for(int i=1; i<=xn; i++){
                    while(true){
                        memset(visx,0,sizeof(visx));
                        memset(visy,0,sizeof(visy));
                        minz = inf;
                        if(dfs(i))break;

                        for(int j=1; j<=xn; j++) if(visx[j])wx[j] -= minz;
                        for(int j=1; j<=xm; j++)if(visy[j])wy[j] += minz;
                    }
                }
                int ans = 0;
                for(int i=1; i<=xn; i++){
                    if(linkx[i]>0){
                        ans -= mp[i][linkx[i]];
                    }
                }
                return ans;

            }
int main(){
            int T;  cin>>T;
            while(T--){
                int n,m;
                scanf("%d%d", &n, &m);
                for(int i=1; i<=n; i++){
                    for(int j=1; j<=m; j++){
                        scanf("%d", &t[i][j]);
                    }
                }
                for(int i=1; i<=n; i++){
                    for(int j=1; j<=m; j++){
                        for(int k=1; k<=n; k++){
                            mp[i][(j-1)*n + k] = - k * t[i][j];
                        }
                    }
                }
                xn = n,xm = m*n;

                int ans = km();
                printf("%.6f
", ans *1.0/n);
            }

            return 0;
}