Support Vector Regression(SVR) 资料
[机器学习]回归--Support Vector Regression(SVR)
https://blog.csdn.net/zwqjoy/article/details/80251707
python 机器学习之支持向量机非线性回归SVR模型
https://www.jb51.net/article/163973.htm
5.4 SVR回归(时间序列分析)
https://blog.csdn.net/weixin_46649052/article/details/112757857
python中sklearn.svm.SVR,模型预测得出的结果都是一个值
https://ask.csdn.net/questions/262144
SVM算法的主要优点:
1) 解决高维特征的分类问题和回归问题很有效,在特征维度大于样本数时依然有很好的效果。
2) 仅仅使用一部分支持向量来做超平面的决策,无需依赖全部数据。
3) 有大量的核函数可以使用,从而可以很灵活的来解决各种非线性的分类回归问题。
4)样本量不是海量数据的时候,分类准确率高,泛化能力强。
SVM算法的主要缺点:
1) 如果特征维度远远大于样本数,则SVM表现一般。
2) SVM在样本量非常大,核函数映射维度非常高时,计算量过大,不太适合使用。
3)非线性问题的核函数的选择没有通用标准,难以选择一个合适的核函数。
4)SVM对缺失数据敏感。
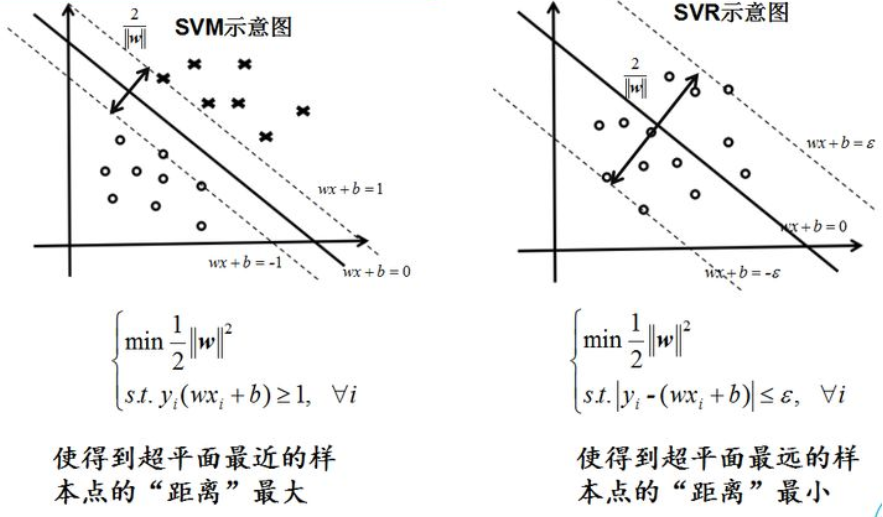
SVM分类,就是找到一个平面,让两个分类集合的支持向量或者所有的数据(LSSVM)离分类平面最远;
SVR回归,就是找到一个回归平面,让一个集合的所有数据到该平面的距离最近。
SVR是支持向量回归 (support vector regression) 的英文缩写,是支持向量机(SVM)的重要的应用分支。
传统回归方法当且仅当回归 f(x) 完全等于 y 时才认为预测正确,如线性回归中常用 (f(x)-y)2 来计算其损失。
而支持向量回归则认为只要 f(x) 与 y 偏离程度不要太大,既可以认为预测正确,不用计算损失,具体的,就是设置阈值 α ,只计算 |f(x)-y|>α 的数据点的 loss,如下图所示,阴影部分的数据点我们都认为该模型预测准确了,只计算阴影外的数据点的 loss:
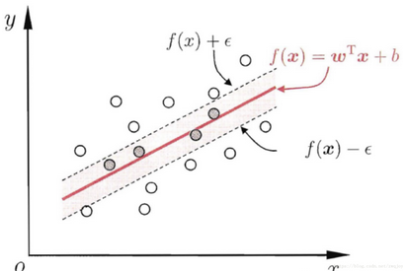
图 1
数据处理
preprocessing.scale()作用:
scale()是用来对原始样本进行缩放的,范围可以自己定,一般是[0,1]或[-1,1]。
缩放的目的主要是
1)防止某个特征过大或过小,从而在训练中起的作用不平衡;
2)为了计算速度。因为在核计算中,会用到内积运算或exp运算,不平衡的数据可能造成计算困难。
对于SVM算法,我们首先导入sklearn.svm中的SVR模块。SVR()就是SVM算法来做回归用的方法(即输入标签是连续值的时候要用的方法),通过以下语句来确定SVR的模式(选取比较重要的几个参数进行测试。随机选取一只股票开始相关参数选择的测试)。
svr = SVR(kernel=’rbf’, C=1e3, gamma=0.01)
kernel:核函数的类型,一般常用的有’rbf’,’linear’,’poly’,等如图所示,发现使用rbf参数时函数模型的拟合效果最好。

图2 函数参数“Linear”,“RBF”,“Poly”对模型的拟合效果图
C:惩罚因子。
C表征你有多么重视离群点,C越大越重视,越不想丢掉它们。C值大时对误差分类的惩罚增大,C值小时对误差分类的惩罚减小。当C越大,趋近无穷的时候,表示不允许分类误差的存在,margin越小,容易过拟合;当C趋于0时,表示我们不再关注分类是否正确,只要求margin越大,容易欠拟合。如图所示发现当使用1e3时最为适宜。 
gamma:
是’rbf’,’poly’和’sigmoid’的核系数且gamma的值必须大于0。随着gamma的增大,存在对于测试集分类效果差而对训练分类效果好的情况,并且容易泛化误差出现过拟合。如图发现gamma=0.01时准确度最高。
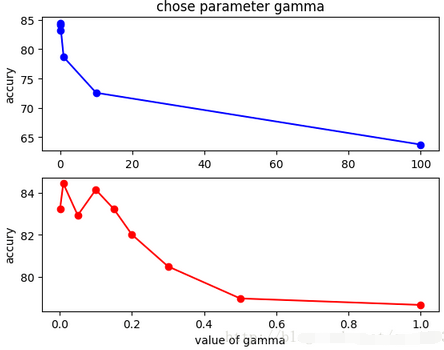
value of gamma
参数gamma与准确度的关系图
用的数据是公司内部不同的promotion level所对应的薪资
https://github.com/lucko515/regression-python/archive/master.zip
REF
https://www.zhihu.com/question/29165683
https://blog.csdn.net/zwqjoy/article/details/80251707
https://blog.csdn.net/qq_16633405/article/details/70243030
https://github.com/lucko515/regression-python