Trie树
Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树,数字的字典树是一个10叉树。
Trie树与二叉搜索树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀(prefix),也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
Trie树可以利用字符串的公共前缀来节约存储空间,如下图所示,该Trie树用11个节点保存了8个字符串tea,ted,ten,to,A,i,in,inn。
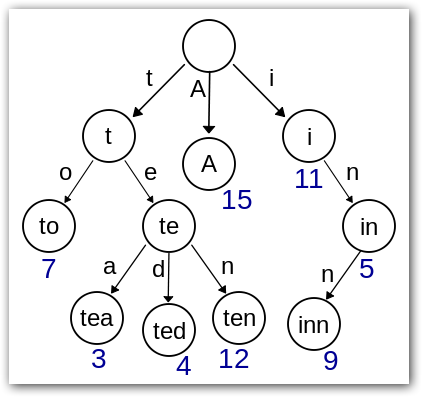
我们注意到Trie树中,字符串tea,ted和ten的相同的前缀(prefix)为"te",如果我们要存储的字符串大部分都具有相同的前缀(prefix),那么该Trie树结构可以节省大量内存空间,因为Trie树中每个单词都是通过character by character方法进行存储,所以具有相同前缀单词是共享前缀节点的。
当然,如果Trie树中存在大量字符串,并且这些字符串基本上没有公共前缀,那么相应的Trie树将非常消耗内存空间,Trie的缺点是空指针耗费内存空间。
Trie树的基本性质可以归纳为:
(1)根节点不包含字符,除根节点外的每个节点只包含一个字符。
(2)从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
(3)每个节点的所有子节点包含的字符串不相同。
三分搜索树:
前面,我们介绍了Trie树结构,它的实现简单但空间效率低。如果要支持26个英文字母,每个节点就要保存26个指针,假若我们还要支持国际字符、标点符号、区分大小写,内存用量就会急剧上升,以至于不可行。
由于节点数组中保存的空指针占用了太多内存,我们遇到的困难与此有关,因此可以考虑改用其他数据结构去代替,比如用hash map。然而,管理成千上万个hash map肯定也不是什么好主意,而且它使数据的相对顺序信息丢失,所以我们还是去看看另一种更好解法吧——Ternary Tree。
接下来,我们将介绍三叉搜索树,它结合字典树的时间效率和二叉搜索树的空间效率优点。
和Trie类似,由于三叉搜索树每个节点只有三个叉,所以我们在进行节点插入操作时,只需判断插入的字符与当前节点的关系(少于,等于或大于)插入到相应的节点就OK了。
我们使用之前的例子,把字符串AB,ABBA,ABCD和BCD插入到三叉搜索树中,首先往树中插入了字符串AB,接着我们插入字符串ABCD,由于ABCD与AB有相同的前缀AB,所以C节点都是存储到B的CenterChild中,D存储到C的CenterChild中;当插入ABBA时,由于ABBA与AB有相同的前缀AB,而B字符少于字符C,所以B存储到C的LeftChild中;当插入BCD时,由于字符B大于字符A,所以B存储到C的RightChild中。
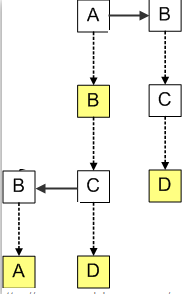
我们注意到插入字符串的顺序会影响三叉搜索树的结构,为了取得最佳性能,字符串应该以随机的顺序插入到三叉树搜索树中,尤其不应该按字母顺序插入,否则对应于单个Trie
节点的子树会退化成链表,极大地增加查找成本。当然我们还可以采用一些方法来实现自平衡的三叉树。
由于树是否平衡取决于单词的读入顺序,如果按排序后的顺序插入,则该方式生成的树是最不平衡的。单词的读入顺序对于创建平衡的三叉搜索树很重要,所以我们通过选择一个排序后数据集合的中间值,并把它作为开始节点,通过不断折半插入中间值,我们就可以创建一棵平衡的三叉树。