壹 ❀ 引
本题来自LeetCode198. 打家劫舍,难度中等,也很有意思,是一道教小偷如何偷窃最大金额的题,题目描述如下:
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。提示:
- 0 <= nums.length <= 100
- 0 <= nums[i] <= 400
让我们简单分析题意,然后想办法实现它。
贰 ❀ 动态规划
本题其实是一道标准的动态规划题目,以局部最优解来求出全局最优解。假设给你一个非有序的数组,让你求出数组中的最小值,不允许排序,不允许使用Math.min你还能怎么做呢?这里就可以借用动态规划。
假设有个数组[3,0,2,4,1],我们可以假设数组第0位就是最小值(min),然后开始从第一位开始遍历(i=1),比较nums[i]与min,如果nums[i]更小,那我们就更新min,反之不用更新,i自增。
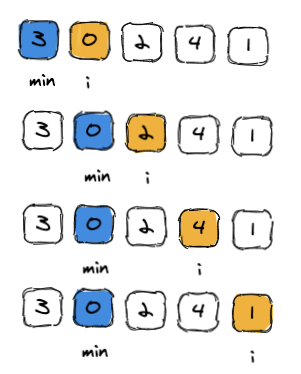
因为min的存在,我们要知道到第i位的最小值,其实只需要比较num[i]和min谁更小即可,因为min已经包含了i-1之前所有位数的最小值,这大概就是一个动态规划最基本的例子。
let findMin = function (nums) {
let min = nums[0];
for (let i = 1; i < nums.length; i++) {
if (nums[i] < min) {
min = nums[i];
}
};
return min;
}
让我们回到问题本身,提取下题目信息,小偷不能连着偷两家,所以从偷第一家的时候,就存在两种情况。我们把这个问题先简单化,比如[1,4,2]。
第一种情况,小偷从第一家开始偷,然后偷第三家。
第二种情况,小偷从第二家开始偷。
我们假设到dp[i]是能偷到的最大收益,偷到第三家的时候,能偷到的最大收益是以上两种偷法之间的最大值,也就是:
// i=2时
// dp[i-1]是直接偷第二家的收益
// dp[i-2]是直接偷第一家的收益
dp[i] = Math.max(dp[i-1], dp[i - 2] + nums[i]);
翻译过来就是,偷到第三家时,是第一家的收益加上第三家自己(nums[2])大,还是直接偷第二家的收益大。
为了能让整个数组套用上面的动态转移方程,当我们遍历时,i得从2开始,那这就有个问题,假设我们数组一共就2位[1,4],我们定义一个dp数组也是2位,很明显当i=1时,i-2越界了。
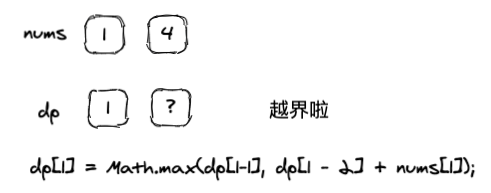
没关系,我们可以故意让dp数组多一位,目的就是为了解决这个越界问题,比如这样:

为了套用动态转移方程,我们初始化了dp[0]为0,当偷到第二家时,其实就是求dp[i] = Math.max(1,0 + 4),4更大。虽然有点魔幻,但找出动态转移方程,套用公式,这就是动态问题的一般解决思路。
让我们实现这段代码:
/**
* @param {number[]} nums
* @return {number}
*/
let rob = function (nums) {
let n = nums.length;
if (n === 0) {
return 0;
};
if (n === 1) {
return nums[0];
};
// 在nums长度基础上加1,因为我们要预设一个0便于套公式
let dp = new Array(n + 1);
dp[0] = 0;
dp[1] = nums[0];
// i从2开始套公式
for (let i = 2; i <= n; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
};
return dp[n];
};
需要注意的有两个点是,第一个是i<=n而不是i<n,原因很简单,比如我们传入[1,4],i一开始就是2,2<2不满足,我们都无法求出偷第二家收益是多少。第二个点是,我们最终加上的是[nums[i-1]],因为i=2其实是站在dp数组的角度多加了一位,对于nums自身而言,下标最大才是1,所以需要减去1才是正确的对应关系。
我们在前面说,因为套用公式为了满足i-2,所以i从2开始,其实还有另一种做法,比如当i=1时,其实是在偷第二家,假设数组为[1,4],此时就是在区分到底是偷第一家划算还是第二家划算,所以我们可以在i<2之前专门做额外的处理,当i超过2之后再套用公式,比如这样:
let n = nums.length;
if (n === 0) {
return 0;
};
if (n === 1) {
return nums[0];
};
// 因为对于i<2做了额外处理,这里就不额外创建空间了
let dp = new Array(n);
// dp数组直接与nums对齐
dp[0] = nums[0];
for (let i = 1; i < n; i++) {
if (i < 2) {
// 小于2,那就是第一家和第二家比较收益
dp[i] = Math.max(dp[i - 1], nums[i]);
} else {
// 超过2家,套公式
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
};
// 这里是dp的最后一位,所以是长度-1
return dp[n - 1];
思路其实完全相同,只是对于2的处理方式不同,那么本文就到这里了。