AtCoder Beginner Contest 146

目录

• A - Can't Wait for Holiday
• B - ROT N
• C - Buy an Integer
• D - Coloring Edges on Tree
• E - Rem of Sum is Num
• F - Sugoroku

A - Can't Wait for Holiday

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
string s;
int main() {
    cin >> s;
    if (s == "SAT") cout << 1 << endl;
    if (s == "FRI") cout << 2 << endl;
    if (s == "THU") cout << 3 << endl;
    if (s == "WED") cout << 4 << endl;
    if (s == "TUE") cout << 5 << endl;
    if (s == "MON") cout << 6 << endl;
    if (s == "SUN") cout << 7 << endl;
    return 0;
}

B - ROT N

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
int n;
string s;
int main() {
    cin >> n >> s;
    for (int i = 0; i < s.size(); i++) {
        cout << char((s[i] - 'A' + n) % 26 + 'A');
    }
    cout << endl;
    return 0;
}

C - Buy an Integer

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
LL A, B, X;
int main() {
    cin >> A >> B >> X;
    int len = -1;

    for (int i = 1; i <= 20; i++) {
        if (A * (LL)pow(10, i - 1) + B * (LL)i > X) {
            len = i - 1;
            break;
        }
    }
    if (len == 0)
        cout << 0 << endl;
    else if (len >= 10 || len == -1) {
        cout << 1000000000 << endl;
    } else {
        X -= B * len;
        if (X / A > 1e9)
            cout << 1000000000 << endl;
        else
            cout << min(X / A, (LL)pow(10, len ) - 1) << endl;
    }
    return 0;
}

D - Coloring Edges on Tree

给出一个n个节点的树，问需要多少颜色才能使得每个点连的边都是不同的颜色，并给出一种涂色方案

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
int n, cnt;
struct node {
    int u, v;
    int color;
} E[N];
vector<pair<int,int>> mp[N];
void dfs(int now, int fa, int color) {
    int last = 0;
    for (int i = 0; i < mp[now].size(); i++) {
        int ne = mp[now][i].first;
        int id = mp[now][i].second;
        if (ne == fa) continue;
        int flag = 1;
        for (int j = last+1; j <= cnt; j++) {
            if (j == color) continue;
            E[id].color = j;
            flag = 0;
            break;
        }
        if (flag) {
            cnt++;
            E[id].color = cnt;
        }
        last = E[id].color;
        dfs(ne, now, E[id].color);
    }
}

int main() {
    cin >> n;
    for (int i = 0; i < n-1; i++) {
        scanf("%d%d", &E[i].u, &E[i].v);
        mp[E[i].u].push_back({E[i].v,i});
        mp[E[i].v].push_back({E[i].u,i});
    }
    dfs(1, 0, 0);
    printf("%d
", cnt);
    for (int i = 0; i < n-1; i++) {
        printf("%d
", E[i].color);
    }
    return 0;
}

E - Rem of Sum is Num

给出一个数组，找出符合以下条件的子区间的个数：

这个子区间的和 % k ==（这个区间的数字个数)。

类似的题目都要想到处理前缀和，然后对前缀和取模

但是又不能枚举，考虑对式子进行转化：

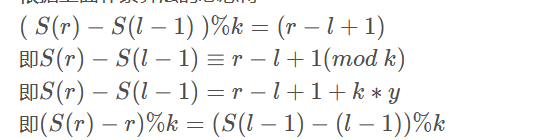
式子来自：https://blog.csdn.net/qq_43408238/article/details/103484868

所以转化为寻找如上式子的子区间个数，但是要注意取模不可能超过k，所以需要利用类似滑动窗口的东西，限制个数

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
LL f[N];
map<LL, LL> mp;
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        scanf("%lld", &f[i]);
        f[i] += f[i - 1];
    }
    for (int i = 1; i <= n; ++i) {
        f[i] = (f[i] - i) % m;
    }
    m--;
    m = min(m, n);
    for (int i = 0; i < m; i++) {
        mp[f[i]]++;
    }
    LL sum = 0;
    for (int i = m; i <= n; ++i) {
        mp[f[i]]++;
        sum += mp[f[i - m]] - 1;
        mp[f[i - m]]--;
    }
    for (int i = n - m + 1; i <= n; ++i) {
        sum += mp[f[i]] - 1;
        mp[f[i]]--;
    }
    cout << sum;

    return 0;
}

F - Sugoroku

单调队列优化DP

给出一个长度为n+1的01字符串，0可以走，1不能走，现在从0号点走到n号点，每次可以跳最多m步，问最少跳几次可以到达n点，输出每次跳的步数

dp求解，类似lis的更新方法：

dp[i]=min(dp[j]+1,dp[i])

但是n为1e5，无法采用n2的算法，所以可以利用单调队列维护长度为m的区间内的dp值的最小值，然后直接转化即可

至于输出路径，利用pre数组维护即可

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
int n, m;
int dp[N], q[N],pre[N];
string s;
int main() {
    cin >> n >> m;
    cin >> s;
    int hh = 0, tt = 0;
    for (int i = 0; i <= m; i++) {
        if (s[i] == '0') dp[i] = 1, pre[i] = 0;
        else dp[i] = 0x3f3f3f3f;
        if (hh <= tt && i - m + 1 > q[hh]) hh++;
        while (hh <= tt && dp[q[tt]] > dp[i]) tt--;
        q[++tt] = i;
    }
     hh++;
    for (int i = m+1; i <= n; i++) {
        dp[i] = 0x3f3f3f3f;
        if (s[i] == '0') dp[i] = min(dp[q[hh]] + 1,dp[i]),pre[i]=q[hh];
        else dp[i] = 0x3f3f3f3f;
        if (hh <= tt && i - m + 1 > q[hh]) hh++;
        while (hh <= tt && dp[q[tt]] > dp[i]) tt--;
        q[++tt] = i;
    }
    stack<int> st;
    //for (int i = 0; i <= n; i++) cout << pre[i] << ' ';
    //cout << endl;
    if (dp[n] != 0x3f3f3f3f) {
        int now = n;
        while (now!=0) {
            st.push(now - pre[now]);
            now = pre[now];
        }
        while (!st.empty()) {
            cout << st.top() << ' ';
            st.pop();
        }
        cout << endl;
        } else
            cout << -1 << endl;
    return 0;
}