Codeforces Round #699 (Div. 2)

目录

• A. Space Navigation
• B. New Colony
• C. Fence Painting
• D. AB Graph
• E. Sorting Books
• F. AB Tree

A. Space Navigation

大意：

给出一个字符串，代表飞船从原点开始的前进方向，问能否经过删掉几个字符，使得飞船最终能够到达((x,y))点

思路：

直接算横纵方向上能达到的最远点即可

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
int const MAXN = 2e5 + 10;
int n, m, T;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> T;
    while (T--) {
        cin >> n >> m;
        string s;
        cin >> s;
        int U = 0, D = 0, L = 0, R = 0;
        for (int i = 0; i < s.size(); ++i) {
            if (s[i] == 'R') R++;
            if (s[i] == 'D') D++;
            if (s[i] == 'L') L++;
            if (s[i] == 'U') U++;
        }
        int flg = 1;
        if (n > 0 && R < n) flg = 0;
        if (n < 0 && L < abs(n)) flg = 0;
        if (m > 0 && U < m) flg = 0;
        if (m < 0 && D < abs(m)) flg = 0;
        if (flg)
            cout << "YES
";
        else
            cout << "NO
";
    }
    return 0;
}

B. New Colony

大意：

给出一个长度为n的数组，代表n座山的高度h，n和h都在1到100之间

每次都从第一座山推下一个巨石，如果巨石所在的山峰比下一座要矮，那么巨石停留在当前山峰，并使得当前山峰高度+1，否则就一直往下滚，直到滚出n

问第k个巨石停止的位置，如果滚出n就输出-1，k<=1e9

思路：

虽然k很大，但是n和h都很小，所以前面直接暴力模拟即可

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
int t, n, k;
int a[N];
int main() {
    cin >> t;
    while (t--) {
        cin >> n >> k;
        for (int i = 1; i <= n; i++) cin >> a[i];
        int res = -1;
        for (int i = 1; i <= k; i++) {
            res = -1;
            for (int j = 1; j <= n - 1; j++) {
                if (a[j] < a[j + 1]) {
                    a[j]++;
                    res = j;
                    break;
                }
            }
            if (res == -1) break;
        }
        cout << res << endl;
    }
    return 0;
}

C. Fence Painting

大意：

给出两个数组，代表n个篱笆原来的颜色和将要涂成的颜色

现在按顺序前来m个画师，他们都会将任意一个篱笆变成自己代表的颜色

问能否在这m个画师都按顺序完成作画后，使得n个篱笆都会变成要涂的颜色

如果能，输出每个画手画的是哪个篱笆

思路：

首先看有几个篱笆要变色，然后看是否有这么多个画手可以让他变色，而对于不需要的画手，可以直接让他画到最后一个画手要画的位置，然后让最后一个画手涂上颜色即可，所以必须要保证最后一个画手可以画画,也就是b数组中有这个画手代表的颜色

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;
int const N = 1e5 + 10;
int n, m, T;
int a[N], b[N], c[N];
map<int, vector<int>> pos;
int f[N];
int ans[N];
int main() {
    cin >> T;
    while (T--) {
        cin >> n >> m;
        for (int i = 1; i <= n; i++) cin >> a[i];
        for (int i = 1; i <= n; i++) cin >> b[i];
        for (int i = 1; i <= m; i++) cin >> c[i];
        for (int i = 1; i <= n; ++i) {
            pos[i].clear();
            f[i] = 0;
        }
        int pos_m = 0;
        for (int i = 1; i <= n; i++) {
            if (b[i] == c[m]) pos_m = i;
            if (a[i] == b[i]) continue;
            pos[b[i]].push_back(i);
            f[b[i]] = i;
        }

        if (f[c[m]] == 0) {
            f[c[m]] = pos_m;

        } else {
            pos[c[m]].pop_back();
        }

        if (f[c[m]] == 0) {
            cout << "No" << endl;
            continue;
        }

        for (int i = 1; i < m; ++i) {
            if (pos[c[i]].size()) {
                ans[i] = pos[c[i]][pos[c[i]].size() - 1];
                pos[c[i]].pop_back();
            } else {
                ans[i] = f[c[m]];
            }
        }
        ans[m] = f[c[m]];
        int flag = 0;
        for (int i = 1; i <= n; ++i) {
            if (pos[i].size()) {
                flag = 1;
            }
        }
        if (flag)
            cout << "No" << endl;
        else {
            cout << "Yes" << endl;
            for (int i = 1; i <= m; i++) {
                cout << ans[i] << " ";
            }
            cout << endl;
        }
    }
    return 0;
}

D. AB Graph

大意：

给出一个完全图，每条边上要么是a要么是b，问能否得到一条路径，使得这条路径上的字符是一个回文串

思路：

首先如果i点和j点之间的两条边相等，都是a或者都是b，那么一定可以组成回文（只需要反复横跳即可）

否则如果m是奇数，那么也一定可以组成回文（假设i到j是a，j到i是b，那么还是反复横跳，得到ababa...）

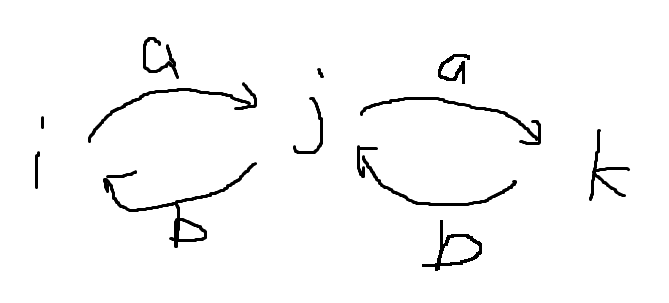
现在就剩下了m是偶数，那么如果三个点之间的关系如下：

那么一定可以形成回文，因为如果((m/2)mod2==1),那么可以从i到j再到k再到j再到i，如此反复，得到aabbaa的形式

否则可以从j到i再到k，得到baab的形式

如果没有这样的关系，那么就相当于一直在ababab的绕圈子，不可能得到回文

#include <bits/stdc++.h>

using namespace std;

const int N = 1e3 + 5;
typedef long long LL;
int t, n, m;
char mp[N][N];
int main() {
    cin >> t;
    while (t--) {
        cin >> n >> m;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                cin >> mp[i][j];
            }
        }
        int flag = 0;
        int res1 = 0, res2 = 0, res3 = 0;
        for (int i = 1; i <= n && flag == 0; i++) {
            for (int j = 1; j <= n && flag == 0; j++) {
                if (i == j) continue;
                if (mp[i][j] == mp[j][i]) {
                    res1 = i, res2 = j;
                    flag = 1;
                }
            }
        }
        if (flag) {
            cout << "YES" << endl;
            for (int i = 0; i < m+1; i++) {
                if (i % 2  == 0)
                    cout << res1 << ' ';
                else
                    cout << res2 << ' ';
            }
            cout << endl;
            continue;
        }
        if (m%2) {
            cout << "YES" << endl;
            for (int i = 1; i <= m+1; i++) {
                if (i % 2 == 0)
                    cout << 1 << ' ';
                else
                    cout << 2 << ' ';
            }
            cout << endl;
            continue;
        }

        int flag1, flag2, flag3 = 0;
        for (int i = 1; i <= n && flag3 == 0; i++) {
            flag1 = flag2 = 0;
            res1 = i, res2 = 0, res3 = 0;
            for (int j = 1; j <= n && flag3 == 0; j++) {
                if (i == j) continue;
                if (mp[i][j] == 'b' && mp[j][i] == 'a') flag1 = 1, res2 = j;
                if (mp[i][j] == 'a' && mp[j][i] == 'b') flag2 = 1, res3 = j;
                if (flag1 && flag2) {
                    flag3 = 1;
                }
            }
        }
        if (flag3) {
            cout << "YES" << endl;
            if ((m / 2)  % 2 ) {
                int bb = 1;
                for (int i = 1; i <= m+1; i++) {
                    if (i % 2 ) {
                        if (bb) {
                            cout << res2 << ' ';
                            bb = 0;
                        } else {
                            cout << res3 << ' ';
                            bb = 1;
                        }
                    } else
                        cout << res1 << ' ';
                }
            } else {
                int bb = 1;
                for (int i = 1; i <= m+1; i++) {
                    if (i % 2  == 0) {
                        if (bb) {
                            cout << res2 << ' ';
                            bb = 0;
                        } else {
                            cout << res3 << ' ';
                            bb = 1;
                        }
                    } else
                        cout << res1 << ' ';
                }
            }
            cout << endl;
        }
        else{
            cout << "NO" << endl;
        }
    }
    return 0;
}

E. Sorting Books

大意：

给出n个书的种类，现在需要只能每次选择一本书，然后扔到最后面，问最少多少次操作可以将每个种类的书都放到一块

思路：

首先需要想到应该是留下来的数尽可能多

那么可以处理出每个数出现的区间，那么可以转化为留下不想交的区间，然后使得这些区间中不需要删掉的点最多

这样dp O(n)的算法扫几遍即可

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
int n, a[N], l[N], r[N], cnt[N], ne[N], dp[N];
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        if (!l[a[i]]) l[a[i]] = i;
        r[a[i]] = i;
    }
    for (int i = n; i >= 1; i--) {
        cnt[a[i]]++;
        ne[i] = max(ne[i + 1], cnt[a[i]]);
    }
    int res = 0;
    for (int i = 1; i <= n; i++) {
        dp[i] = dp[i - 1];
        if (r[a[i]] == i) dp[i] = max(dp[i], dp[l[a[i]] - 1] + cnt[a[i]]);
        res = max(res, dp[i] + ne[i + 1]);
    }
    cout << n - res << endl;
    return 0;
}

F. AB Tree

大意：

待补

思路：