【计算几何】点在多边形内部

问题描述：已知点P(x,y)和多边形Poly，判断点P(x,y)是否在多边形内部。

基本方法：射线法

以点P为端点，向左方作射线L，由于多边形是有界的，所以射线L的左端一定在多边形外部，考虑沿着L从无究远处开始自左向右移动。

遇到和多边形的第一个交点的时候，进入到了多边形的内部，遇到第二个交点的时候，离开了多边形...

因而当L和多边形的交点数目C是奇数的时候，P在多边形内，是偶数，则P在多边形外。

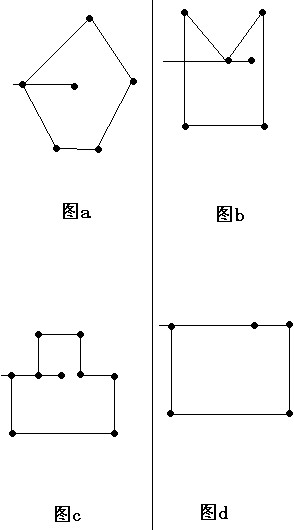
特殊情况分析，如图下图(a),(b),(c),(d)所示。

图(a)中，L和多边形的顶点相交，交点只能计算一个。

图(b)中，L和多边形顶点的交点不应被计算。

图(c)和(d)中，L和多边形的一条边重合，这条边应该被忽略不计。

代码实现如下：

typedef struct Point
{
    int x;
    int y;
}Point;
//  The function will return YES if the point x,y is inside the polygon, or
//  NO if it is not.  If the point is exactly on the edge of the polygon,
//  then the function may return YES or NO.
bool IsPointInPolygon(std::vector<Point> poly,Point pt)
{
    int i,j;
    bool c = false;
    for (i = 0,j = poly.size() - 1;i < poly.size();j = i++)
    {
        if ((((poly[i].y <= pt.y) && (pt.y < poly[j].y)) ||
            ((poly[j].y <= pt.y) && (pt.y < poly[i].y)))
            && (pt.x < (poly[j].x - poly[i].x) * (pt.y - poly[i].y)/(poly[j].y - poly[i].y) + poly[i].x))
        {
            c = !c;
        }
    }
    return c;
}

代码分析：

条件1：((ploy[i].y <= pt.y) && (pt.y < poly[j].y)) || ((ploy[j].y <= pt.y) && (pt.y < poly[i].y))

由于判断过程主要是判断，射线L与多边形每条边是否存在交点，而射线L平行于X轴，因此条件1相当于判断点P在Pi和Pj在垂直距离之间。

条件2: (pt.x < (poly[j].x - poly[i].x) * (pt.y - poly[i].y)/(poly[j].y - poly[i].y) + poly[i].x)

条件2可转换成：(pt.x - poly[i].x) * (poly[j].y - poly[i].y) - (poly[j].x - poly[i].x) * (pt.y - poly[i].y) < 0，相当于向量PiP和向量PiPj的叉积。

当向量PiP和向量PiPj的叉积小于0时，向量PiP在向量PiPj的逆时针方向，相当于向量PiP在向量PiPj的右侧，而射线L由左侧射出，而且点P在Pi和Pj在垂直距离之间，因此，射线L和PiPj的跨立条件成立，相交。

参考资料：

http://alienryderflex.com/polygon/