说到神经网络,大家看到这个图应该不陌生:
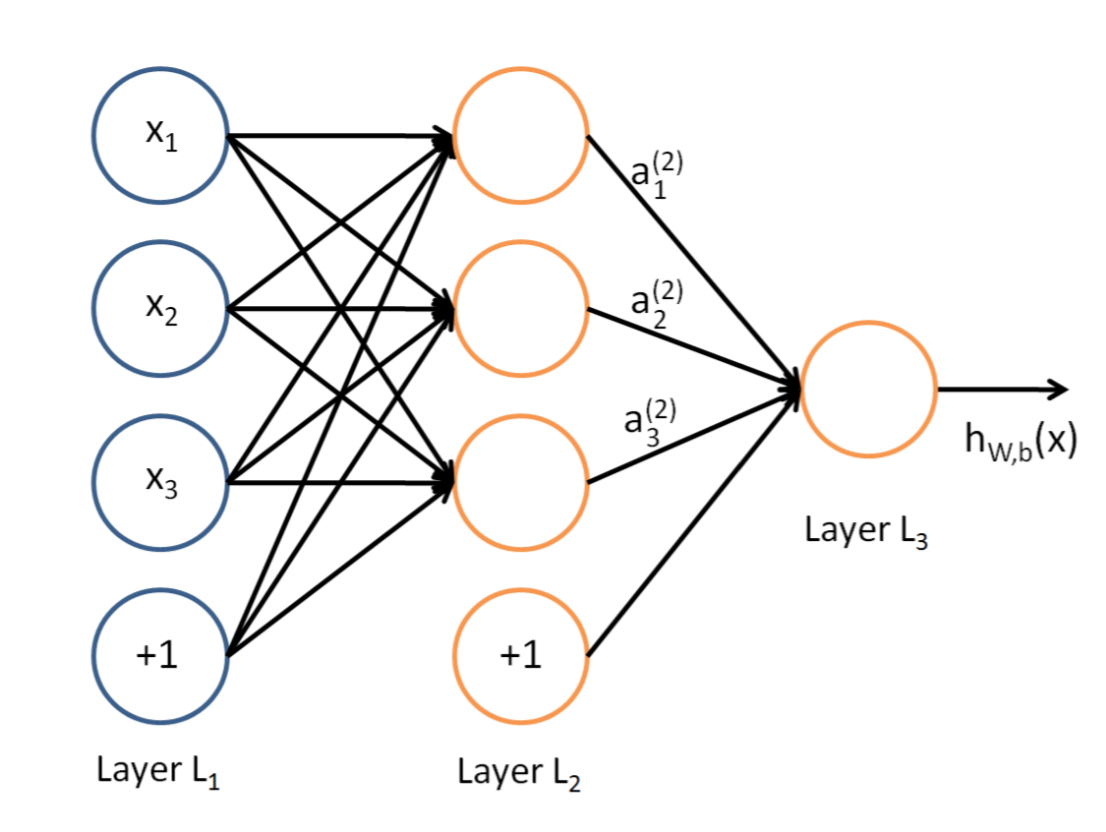
这是典型的三层神经网络的基本构成,Layer L1是输入层,Layer L2是隐含层,Layer L3是隐含层,我们现在手里有一堆数据{x1,x2,x3,…,xn},输出也是一堆数据{y1,y2,y3,…,yn},现在要他们在隐含层做某种变换,让你把数据灌进去后得到你期望的输出。如果你希望你的输出和原始输入一样,那么就是最常见的自编码模型(Auto-Encoder)。可能有人会问,为什么要输入输出都一样呢?有什么用啊?其实应用挺广的,在图像识别,文本分类等等都会用到。如果你的输出和原始输入不一样,那么就是很常见的人工神经网络了,相当于让原始数据通过一个映射来得到我们想要的输出数据,也就是我们今天要讲的话题。
本文直接举一个例子,带入数值演示反向传播法的过程,其实也很简单,感兴趣的同学可以自己推导下试试:)(注:本文假设你已经懂得基本的神经网络构成,如果完全不懂,可以参考Poll写的笔记:[Mechine Learning & Algorithm] 神经网络基础)
假设,你有这样一个网络层:

第一层是输入层,包含两个神经元i1,i2,和截距项b1;第二层是隐含层,包含两个神经元h1,h2和截距项b2,第三层是输出o1,o2,每条线上标的wi是层与层之间连接的权重,激活函数我们默认为sigmoid函数。
现在对他们赋上初值,如下图:
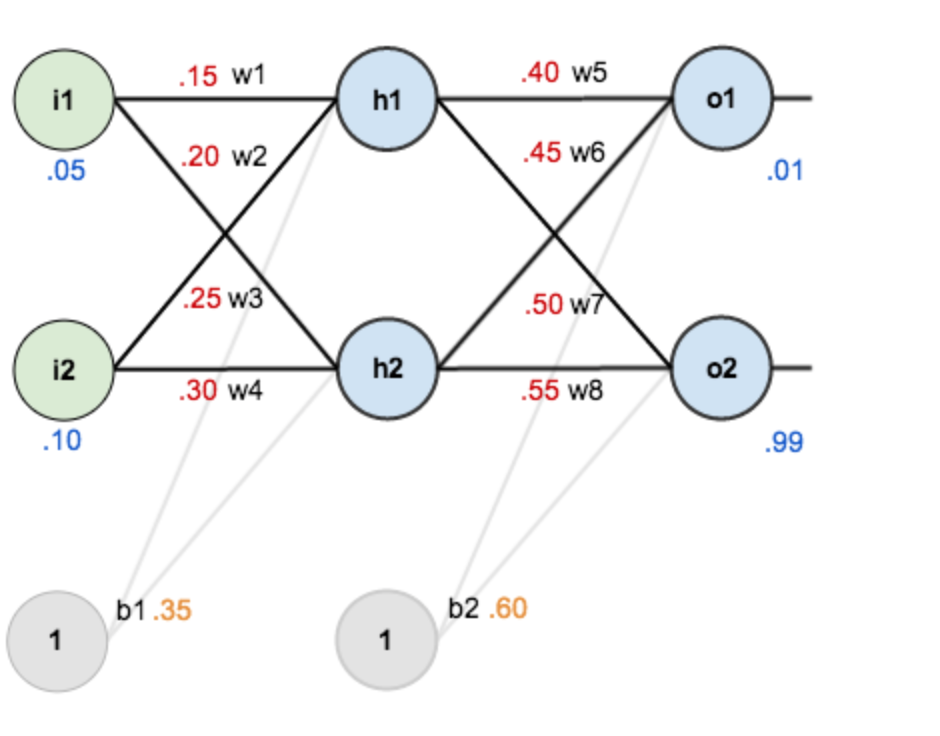
其中,输入数据 i1=0.05,i2=0.10;
输出数据 o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.55
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
Step 1 前向传播
1.输入层—->隐含层:
计算神经元h1的输入加权和:

神经元h1的输出o1:(此处用到激活函数为sigmoid函数):
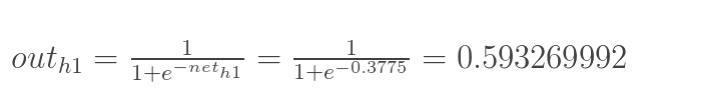
同理,可计算出神经元h2的输出o2:

2.隐含层—->输出层:
计算输出层神经元o1和o2的值:

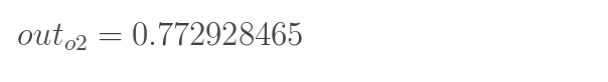
这样前向传播的过程就结束了,我们得到输出值为[0.75136079 , 0.772928465],与实际值[0.01 , 0.99]相差还很远,现在我们对误差进行反向传播,更新权值,重新计算输出。
Step 2 反向传播
1.计算总误差
总误差:(square error)
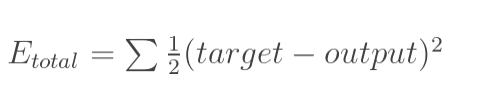
但是有两个输出,所以分别计算o1和o2的误差,总误差为两者之和:


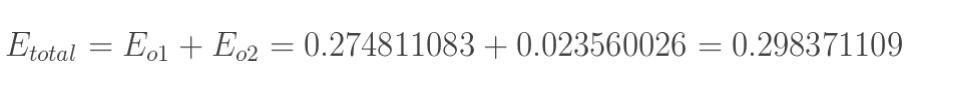
2.隐含层—->输出层的权值更新:
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)

下面的图可以更直观的看清楚误差是怎样反向传播的:

现在我们来分别计算每个式子的值:
计算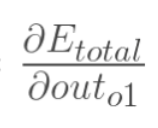 :
:

计算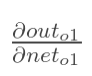 :
:

(这一步实际上就是对sigmoid函数求导,比较简单,可以自己推导一下)
计算 :
:
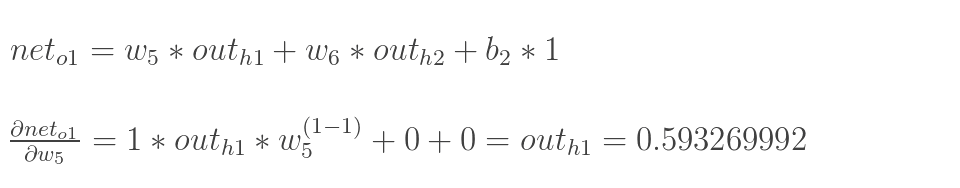
最后三者相乘:

这样我们就计算出整体误差E(total)对w5的偏导值。
回过头来再看看上面的公式,我们发现:

为了表达方便,用 来表示输出层的误差:
来表示输出层的误差:

因此,整体误差E(total)对w5的偏导公式可以写成:

如果输出层误差计为负的话,也可以写成:

最后我们来更新w5的值:
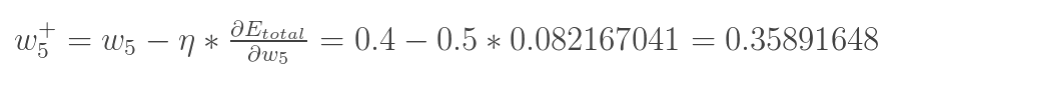
(其中, 是学习速率,这里我们取0.5)
是学习速率,这里我们取0.5)
同理,可更新w6,w7,w8:

3.隐含层—->隐含层的权值更新:
方法其实与上面说的差不多,但是有个地方需要变一下,在上文计算总误差对w5的偏导时,是从out(o1)—->net(o1)—->w5,但是在隐含层之间的权值更新时,是out(h1)—->net(h1)—->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差,所以这个地方两个都要计算。
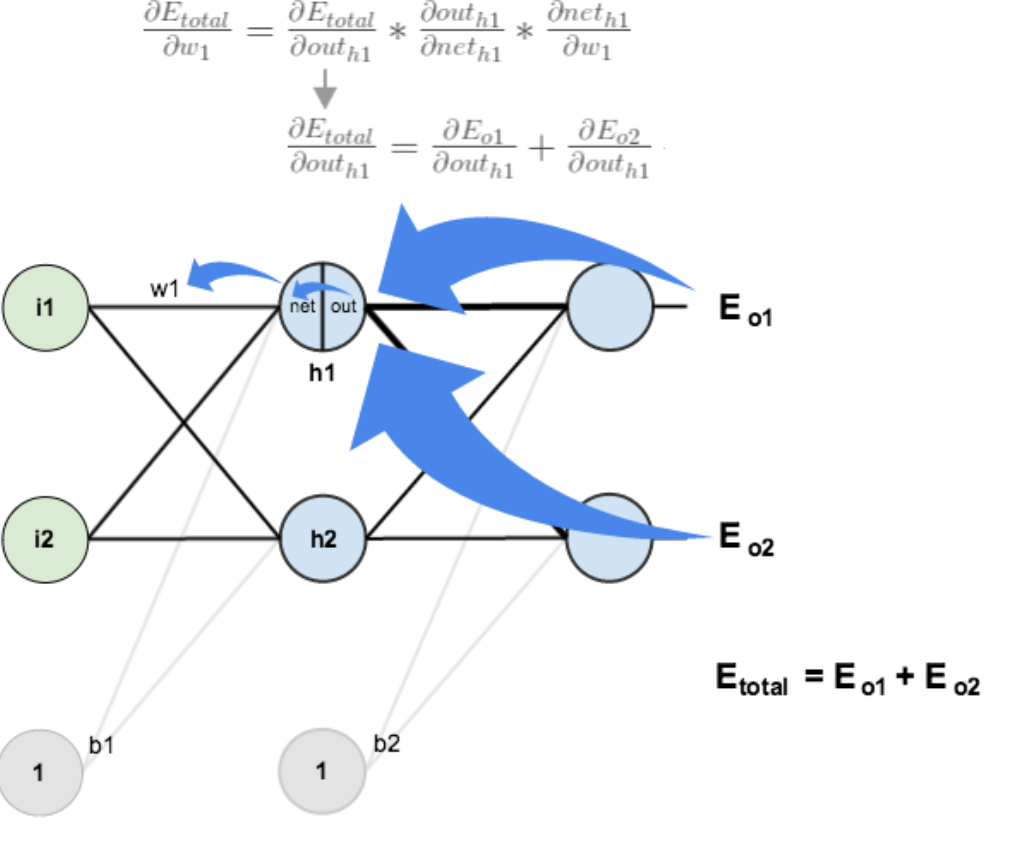
计算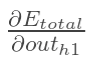 :
:

先计算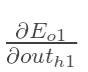 :
:
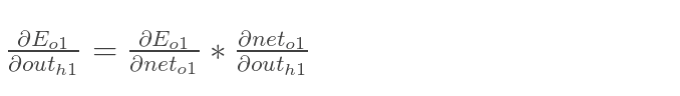

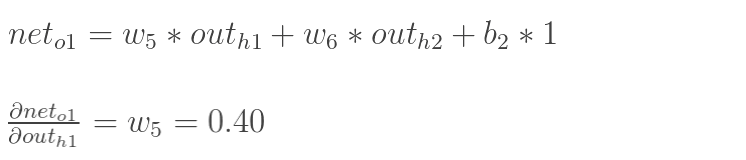
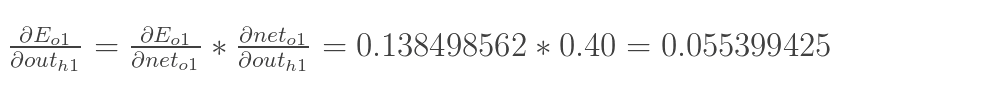
同理,计算出:
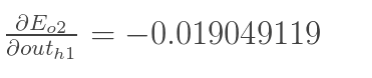
两者相加得到总值:
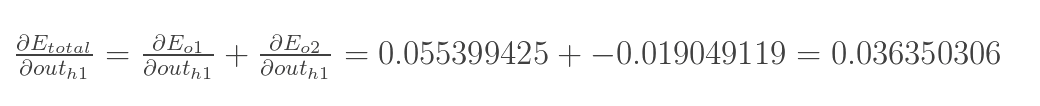
再计算 :
:

再计算 :
:

最后,三者相乘:

为了简化公式,用sigma(h1)表示隐含层单元h1的误差:

最后,更新w1的权值:

同理,额可更新w2,w3,w4的权值:

这样误差反向传播法就完成了,最后我们再把更新的权值重新计算,不停地迭代,在这个例子中第一次迭代之后,总误差E(total)由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为[0.015912196,0.984065734](原输入为[0.01,0.99]),证明效果还是不错的。
BP算法改进
BP算法易形成局部极小而得不到全局最优,训练次数多使得学习效率低,存在收敛速度慢等问题。
传统的BP算法改进主要有两类:
启发式算法:如附加动量法,自适应算法。
数值优化算法:如共轭梯度法、牛顿迭代法等。
1,附加动量项
这是一种广泛用于加速梯度下降法收敛的优化方法。附加动量法面临学习率的选取的困难,进而产生收敛速度与收敛性之间的矛盾。
核心思想:在梯度下降搜索时,若当前梯度下降与之前梯度下降方向相同,则加速搜索,反之则减速搜索。
标准BP算法的参数更新项为:
∆ω(t)= ηg(t)
式中,∆ω(t)为第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代所计算出的梯度。
添加动量项之后,基于梯度下降的参数更新为:
∆ωt= ηgt+α∆ωt-1
式中α被称为动量系数,一般α∈(0,1),α∆ω(t-1)代表之前梯度下降的方向和大小信息对当前梯度下降的调整作用。
2,自适应学习率
核心思想:自适应改变学习率,使其根据环境变化增大或减小。
ηt=σ(t)η(t-1)
上式中,σ(t)为第 t 次迭代时的自适应学习速率因子。
3,引入陡度因子
核心思想:如果在调整进入平坦区后,设法压缩神经元的净输入,使其输出退出激活函数的不饱和区,就可以改变误差函数的形状,从而使调整脱离平坦区。
在原激活函数中引入一个陡度因子λ
1 #coding:utf-8 2 import random 3 import math 4 5 # 6 # 参数解释: 7 # "pd_" :偏导的前缀 8 # "d_" :导数的前缀 9 # "w_ho" :隐含层到输出层的权重系数索引 10 # "w_ih" :输入层到隐含层的权重系数的索引 11 12 class NeuralNetwork: 13 LEARNING_RATE = 0.5 14 15 def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights =None,hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None): 16 self.num_inputs = num_inputs 17 18 self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias) 19 self.output_layer = NeuronLayer(num_outputs, output_layer_bias) 20 21 self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights) 22 self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights) 23 24 def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights): 25 weight_num = 0 26 for h in range(len(self.hidden_layer.neurons)): 27 for i in range(self.num_inputs): 28 if not hidden_layer_weights: 29 self.hidden_layer.neurons[h].weights.append(random.random()) 30 else: 31 self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num]) 32 weight_num += 1 33 34 def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights): 35 weight_num = 0 36 for o in range(len(self.output_layer.neurons)): 37 for h in range(len(self.hidden_layer.neurons)): 38 if not output_layer_weights: 39 self.output_layer.neurons[o].weights.append(random.random()) 40 else: 41 self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num]) 42 weight_num += 1 43 44 def inspect(self): 45 print('------') 46 print('* Inputs: {}'.format(self.num_inputs)) 47 print('------') 48 print('Hidden Layer') 49 self.hidden_layer.inspect() 50 print('------') 51 print('* Output Layer') 52 self.output_layer.inspect() 53 print('------') 54 55 def feed_forward(self, inputs): 56 hidden_layer_outputs = self.hidden_layer.feed_forward(inputs) 57 return self.output_layer.feed_forward(hidden_layer_outputs) 58 59 def train(self, training_inputs, training_outputs): 60 self.feed_forward(training_inputs) 61 62 # 1. 输出神经元的值 63 pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons) 64 for o in range(len(self.output_layer.neurons)): 65 66 # ∂E/∂zⱼ 67 pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o]) 68 69 # 2. 隐含层神经元的值 70 pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons) 71 for h in range(len(self.hidden_layer.neurons)): 72 73 # dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ 74 d_error_wrt_hidden_neuron_output = 0 75 for o in range(len(self.output_layer.neurons)): 76 d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h] 77 78 # ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂ 79 pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input() 80 81 # 3. 更新输出层权重系数 82 for o in range(len(self.output_layer.neurons)): 83 for w_ho in range(len(self.output_layer.neurons[o].weights)): 84 85 # ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ 86 pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho) 87 88 # Δw = α * ∂Eⱼ/∂wᵢ 89 self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight 90 91 # 4. 更新隐含层的权重系数 92 for h in range(len(self.hidden_layer.neurons)): 93 for w_ih in range(len(self.hidden_layer.neurons[h].weights)): 94 95 # ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ 96 pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih) 97 98 # Δw = α * ∂Eⱼ/∂wᵢ 99 self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight 100 101 def calculate_total_error(self, training_sets): 102 total_error = 0 103 for t in range(len(training_sets)): 104 training_inputs, training_outputs = training_sets[t] 105 self.feed_forward(training_inputs) 106 for o in range(len(training_outputs)): 107 total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o]) 108 return total_error 109 110 class NeuronLayer: 111 def __init__(self, num_neurons, bias): 112 113 # 同一层的神经元共享一个截距项b 114 self.bias = bias if bias else random.random() 115 116 self.neurons = [] 117 for i in range(num_neurons): 118 self.neurons.append(Neuron(self.bias)) 119 120 def inspect(self): 121 print('Neurons:', len(self.neurons)) 122 for n in range(len(self.neurons)): 123 print(' Neuron', n) 124 for w in range(len(self.neurons[n].weights)): 125 print(' Weight:', self.neurons[n].weights[w]) 126 print(' Bias:', self.bias) 127 128 def feed_forward(self, inputs): 129 outputs = [] 130 for neuron in self.neurons: 131 outputs.append(neuron.calculate_output(inputs)) 132 return outputs 133 134 def get_outputs(self): 135 outputs = [] 136 for neuron in self.neurons: 137 outputs.append(neuron.output) 138 return outputs 139 140 class Neuron: 141 def __init__(self, bias): 142 self.bias = bias 143 self.weights = [] 144 145 def calculate_output(self, inputs): 146 self.inputs = inputs 147 self.output = self.squash(self.calculate_total_net_input()) 148 return self.output 149 150 def calculate_total_net_input(self): 151 total = 0 152 for i in range(len(self.inputs)): 153 total += self.inputs[i] * self.weights[i] 154 return total + self.bias 155 156 # 激活函数sigmoid 157 def squash(self, total_net_input): 158 return 1 / (1 + math.exp(-total_net_input)) 159 160 161 def calculate_pd_error_wrt_total_net_input(self, target_output): 162 return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input(); 163 164 # 每一个神经元的误差是由平方差公式计算的 165 def calculate_error(self, target_output): 166 return 0.5 * (target_output - self.output) ** 2 167 168 169 def calculate_pd_error_wrt_output(self, target_output): 170 return -(target_output - self.output) 171 172 173 def calculate_pd_total_net_input_wrt_input(self): 174 return self.output * (1 - self.output) 175 176 177 def calculate_pd_total_net_input_wrt_weight(self, index): 178 return self.inputs[index] 179 180 181 # 文中的例子: 182 183 nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3],hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55],output_layer_bias=0.6) 184 for i in range(10000): 185 nn.train([0.05, 0.1], [0.01, 0.09]) 186 print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9)) 187 188 #另外一个例子,可以把上面的例子注释掉再运行一下: 189 190 # training_sets = [ 191 # [[0, 0], [0]], 192 # [[0, 1], [1]], 193 # [[1, 0], [1]], 194 # [[1, 1], [0]] 195 # ] 196 197 # nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1])) 198 # for i in range(10000): 199 # training_inputs, training_outputs = random.choice(training_sets) 200 # nn.train(training_inputs, training_outputs) 201 # print(i, nn.calculate_total_error(training_sets))