概述
在谈堆之前,我们先了解什么是优先队列。我们每天都在排队,银行,医院,购物都得排队。排在队首先处理事情,处理完才能从这个队伍离开,又有新的人来排在队尾。但仅仅这样就能满足我们生活需求吗,明显不能。医院里,患者排队准备看病,这时有个重症患者入队,医生如果按队列的方式一个一个往下处理,等排到这位重病患者时,可能他就因为伤情过重挂了,之后就会引发医患纠纷,这明显不是我们想要的结果。优先队列就成为我们解决此类事情的关键,重病患者入队(挂号),医生根据他的伤情紧急(优先级)优先处理他的病情。

如果非要用专业术语来区分他们二者的区别
- 队列先进先出,后进后出
- 优先队列,出队与入队时的顺序无关,与优先级有关。
堆
了解了优先队列,那这个堆又是什么玩意,可能很多人听过内存堆栈。特别要声明和注意的是,这里的堆仅仅是存储数据的一种结构方式,与内存的堆栈不是一个概念。
- 二叉堆是一颗完全二叉树结构(不懂什么是树的同学请面壁),说的通俗点,堆就是满足一些特殊性质的树,所以二叉堆就是有特殊性质的二叉树。
- 父节点的值大于(小于)两个子节点的值,又称为最大堆和最小堆,我们要定义的是最大堆(最小堆跟他相反)。
实例
我们先来看下什么是满的二叉树
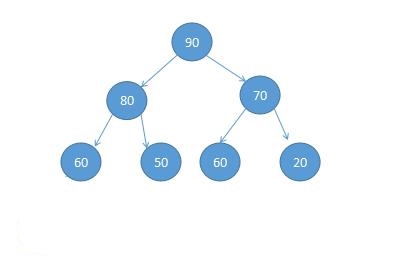
每一层所有节点都有两个儿子结点的二叉树,就叫满的二叉树,计算他节点个数的公式2^3 - 1 = 7。有七个节点
完全二叉树(最大堆)
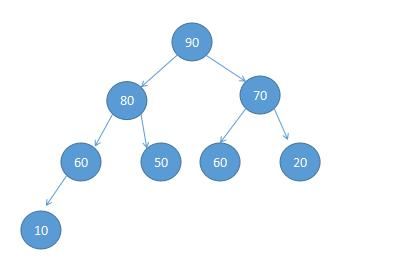
堆和优先队列有什么关系
知道了什么是堆和优先队列,它们之间有什么关系哪。说穿了就一句话,堆是优先队列这种数据结构的一种实现方式。
注意:优先队列可以用不同的底层实现(普通线性结构),时间复杂度不同。
数组实现完全二叉树(最大堆)
也可以定义二叉树来实现完全二叉树,但是通过观察会发现其结构的特点,都是用顺序存储方式存储。从1到n编号,就得到结点的一个线性系列。每一层结点个数恰好是上一层结点个数的2倍,也因此通过一个节点的编号就可以推知他的左右孩子节点的编号。
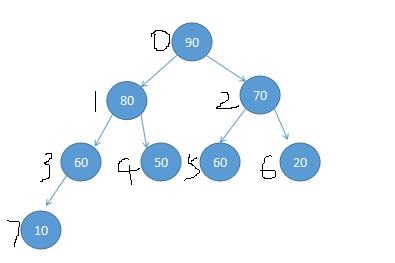
通过分析和数学归纳得出一个结论,很方便的知道他的左右孩子节点和父节点。
- 父节点 parent(i) = (i - 1) / 2,算下结点10的父节点 (7 - 1) / 2 = 3 就是 60
- 左孩子 left child(i) = 2 * i + 1,可以算出 10 的左孩子 7 * 2 + 1 = 15 > 7 (这里的7为最大索引值)没有左孩子这个结点
- 右孩子 right child(i) = 2 * i + 2,可以算出 10 的右孩子 7 * 2 + 2 = 16 > 7 没有右孩子这个结点
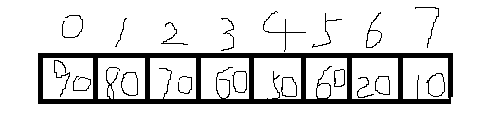
定义一个我们自己的数组Array类,也可以用Java提供的Array
Array类
public class Array<E> { private E[] data; private int size; //构造函数,传入数组的容量capacity构造Array public Array(int capacity) { this.data = (E[]) new Object[capacity]; size = 0; } //无参数构造函数 public Array() { this(10); } //获取数组的个数 public int getSize() { return size; } //获取数组的容量 public int getCapacity() { return data.length; } //数组是否为空 public boolean isEmpty() { return size == 0; } //添加最后一个元素 public void addLast(E e) { add(size,e); } //添加第一个元素 public void addFirst(E e){ add(0,e); } //获取inde索引位置的元素 public E get(int index){ if (index < 0 || index >= size){ throw new IllegalArgumentException("Get failed,index is illegal"); } return data[index]; } public void set(int index,E e){ if (index < 0 || index >= size){ throw new IllegalArgumentException("Get failed,index is illegal"); } data[index] = e; } //获取最后一个元素 public E getLast(){ return this.get(size - 1); } //获取第一个元素 public E getFirst(){ return this.get(0); } //添加元素 public void add(int index,E e){ if (index > size || index < 0){ throw new IllegalArgumentException("add failed beceause index > size or index < 0,Array is full."); } if (size == data.length){ resize(data.length * 2); } for (int i = size - 1; i >= index; i--) { data[i+1] = data[i]; } data[index] = e; size ++; } //扩容数组 private void resize(int newCapacity) { E[] newData = (E[]) new Object[newCapacity]; for (int i = 0; i < size; i++) { newData[i] = data[i]; } data = newData; } public E[] getData() { return data; } //查找数组中是否有元素e public boolean contains(E e){ for (int i = 0; i < size; i++) { if (data[i].equals(e)){ return true; } } return false; } //根据元素查看索引 public int find(E e){ for (int i = 0; i < size; i++) { if (data[i].equals(e)){ return i; } } return -1; } //删除某个索引元素 public E remove(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("detele is fail,index < 0 or index >= size"); } E ret = data[index]; for (int i = index + 1; i < size; i++) { data[i - 1] = data[i]; } size --; data[size] = null; if (size < data.length / 2){ resize(data.length / 2); } return ret; } //删除首个元素 public E removeFirst(){ return this.remove(0); } //删除最后一个元素 public E removeLast(){ return this.remove(size - 1); } //从数组删除元素e public void removeElemen(E e){ int index = find(e); if (index != -1){ remove(index); } } @Override public String toString() { StringBuilder sb = new StringBuilder(""); sb.append(String.format("Array:size = %d,capacity = %d ",size,data.length)); sb.append("["); for (int i = 0; i < size; i++) { sb.append(data[i]); if (i != size - 1){ sb.append(","); } } sb.append("]"); return sb.toString(); } }
有了Array数组类,接下来很快的,把我们刚才描述的事情用代码实现出来之后,在考虑出队和入队的操作,因为父节点要大于或小于他们的子节点。所以我们的节点要能相互比较,在Java继承Comparable类就可以了。
最大堆(MaxHeap类)
public class MaxHeap<E extends Comparable<E>> { private Array<E> data; public MaxHeap(int capacity) { data = new Array<>(capacity); } public MaxHeap() { data = new Array<>(); } //堆里的元素个数 public int size() { return data.getSize(); } //堆是否为空 public boolean isEmpty() { return data.isEmpty(); } //根据一个元素的索引,获取他父亲索引 private int parent(int index) { if (index == 0) { throw new IllegalArgumentException("index - 0 does't have parent."); } return (index - 1) / 2; } //根据一个元素的索引,获取他右孩子的索引 private int leftChild(int index) { return index * 2 + 1; } //根据一个元素的索引,获取他左孩子的索引 private int rightChild(int index) { return index * 2 + 2; } }
向堆中添加一个元素,在堆的内部要进行一个上浮的操作,保证用数组实现的二叉堆还符合我们最大堆的性质(父节点的值大于两个子节点的值)。

82大于他的父节点60,两个结点交换位置,82还大于他的父结点80,两个节点交换位置。80小于现在的父结点90,结束交换。这个操作很多人称为上浮操作(个人认为名称贴切)上浮操作完成。

用代码实现我们刚才的操作,已经知道他父结点的位置(公式),交换两个人的位置就变得很简单,MaxHeap添加函数。
//堆中添加元素 public void add(E e) { data.addLast(e); siftUp(data.getSize() - 1); } //上浮操作 private void siftUp(int i) { while (i > 0 && data.get(parent(i)).compareTo(data.get(i)) < 0) { //交换位置 data.swap(i,parent(i));
i = parent(i) } }
Array类,添加交换位置的函数
public void swap(int i,int j) { if (i < 0 || i >= size || j < 0 || j > size) { throw new IllegalArgumentException("索引越界"); } E t = data[i]; data[i] = data[j]; data[j] = t; }
有添加就有取出,取出堆中元素其实很简单,因为最大堆决定了只取堆顶元素(数组的第一个元素),直接取出即可。困难的是如何维护二叉堆的性质不变。
取出堆顶元素后

取出堆顶元素,剩下两个子树,将两颗子树糅合成一个二叉堆,现在直接将60这个元素作为堆顶,就满足了完全二叉树的性质但并不符合最大堆性质。
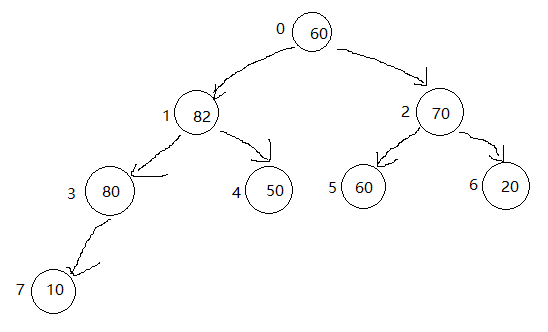
和上浮的操作相反,现在我们要进行下沉的操作,60的左右孩子都比60来得大,要选择左右孩子最大的那个数进行交换,82和60进行交换,80比60来得大,交换他们的位置,10比60来得小,符合二叉堆的性质。交换结束。
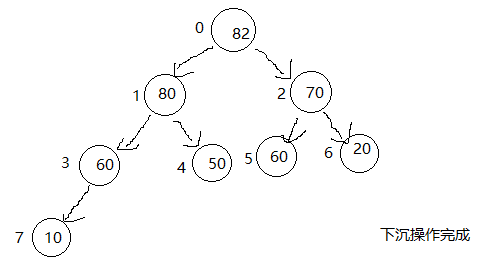
用代码描述刚才取出的操作。
MaxHeap类
//堆中最大元素 public E findMax() { if (data.getSize() == 0) { throw new IllegalArgumentException("堆为空,无法查看值"); } return data.get(0); } //取出堆顶元素 public E extractMax() { E ret = findMax(); data.swap(0,data.getSize() - 1); data.removeLast(); siftDown(0); return ret; } //下沉操作 private void siftDown(int i) { //比较到他左右孩子那个比他大进行交换操作 while (leftChild(i) < data.getSize()) { int j = leftChild(i); if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) //右节点 { j = rightChild(i); } if (data.get(i).compareTo(data.get(j)) >= 0) { break; } data.swap(i,j); i = j; } }
现在我们堆结构基本完成,简单测试一下
Main类
public class Main { public static void main(String[] args) { MaxHeap<Integer> maxHeap = new MaxHeap<>(); int[] nums = {90,80,70,60,50,60,20,10}; for (int i = 0; i < nums.length; i++) { maxHeap.add(nums[i]); } System.out.println("堆顶:" + maxHeap.findMax()); maxHeap.add(82);//添加82 System.out.println("取出堆顶值:" + maxHeap.extractMax()); System.out.println("堆顶:" + maxHeap.findMax());//是否为82 maxHeap.add(85);//添加85 System.out.println("堆顶:" + maxHeap.findMax()); //是否为85 System.out.println("测试结束"); } }
输出
堆顶:90 取出堆顶值:90 堆顶:82 堆顶:85 测试结束
用定义的最大堆去实现一个优先队列就变得十分简单了,优先队列本质上来说还是一个队列,用堆来实现队列的接口。
Queue接口类
public interface Queue<E> { int getSize(); boolean isEmpty(); void enqueue(E e); E dequeue(); E getFront(); }
优先队列(PriorityQueue类)
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> { private MaxHeap<E> maxHeap; public PriorityQueue() { maxHeap = new MaxHeap<>(); } @Override public int getSize() { return maxHeap.size(); } @Override public boolean isEmpty() { return maxHeap.isEmpty(); } @Override public void enqueue(E e) { maxHeap.add(e); } @Override public E dequeue() { return maxHeap.extractMax(); } @Override public E getFront() { return maxHeap.findMax(); } }
实例
在股票市场,很多股民向股票代理打电话,股票代理公司优先处理vip客户(有钱¥)再处理普通的用户。把他们的money当做他们的优先程度
Customer类
public class Customer implements Comparable<Customer> { private int money; private String name; public Customer(int money, String name) { this.money = money; this.name = name; } public int getMoney() { return money; } public void setMoney(int money) { this.money = money; } public String getName() { return name; } public void setName(String name) { this.name = name; } @Override public int compareTo(Customer another) { if (this.money < another.money) { return -1; }else if (this.money > another.money) { return 1; }else { return 0; } } }
Main类
public class Main { public static void main(String[] args) { //优先队列使用示例 Queue<Customer> queue = new PriorityQueue<>(); Random random = new Random(); for (int i = 0; i < 10; i++) { int money = random.nextInt(1000000); queue.enqueue(new Customer(money,"客户" + i )); } while (true) { if (queue.isEmpty()) { break; } Customer customer = queue.dequeue(); System.out.println("优先处理 " + customer.getName() + " 因为他的money为:" + customer.getMoney() + "¥"); } } }
输出
优先处理 客户4 因为他的money为:842917¥ 优先处理 客户7 因为他的money为:628183¥ 优先处理 客户8 因为他的money为:578457¥ 优先处理 客户0 因为他的money为:551270¥ 优先处理 客户1 因为他的money为:538859¥ 优先处理 客户5 因为他的money为:297316¥ 优先处理 客户3 因为他的money为:262908¥ 优先处理 客户9 因为他的money为:250763¥ 优先处理 客户6 因为他的money为:144102¥ 优先处理 客户2 因为他的money为:96273¥
随机数,输出结果不确定。但一定是从大到小排序,如果要从小到大很简单,改比较符即可。这边实现的是最大堆,Java提供的优先队列(PriorityQueue)底层是最小堆。
============================================
如发现错误请留言提醒lz,好及时修改,避免误导别人。拜谢