上篇文章我们介绍了树的概念,今天我们来介绍一种特殊的树——二叉树,二叉树的应用很广,有很多特性。今天我们一一来为大家介绍。
二叉树
顾名思义,二叉树就是只有两个节点的树,两个节点分别为左节点和右节点,特别强调,即使只有一个子节点也要区分它是左节点还是右节点。
常见的二叉树有一般二叉树、完全二叉树、满二叉树、线索二叉树、霍夫曼树、二叉排序树、平衡二叉树、红黑树、B树这么多种类。我们这篇文章中简单介绍一般二叉树、完全二叉树和满二叉树。
一般二叉树
很简单,只要满足子节点数不超过两个的树就是一棵二叉树。长这样:

满二叉树
满二叉树在一般二叉树的基础上要求除了最后一层的节点之外,每一个节点都必须有两个子节点。
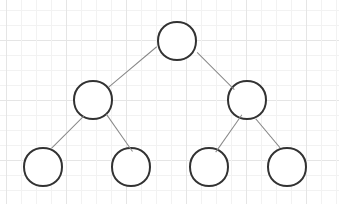
完全二叉树
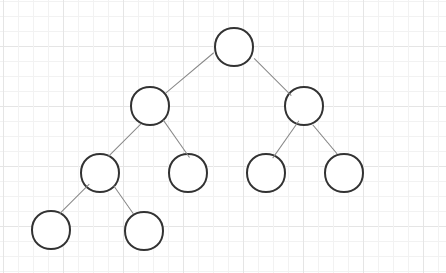
完全二叉树要求从第一层到倒数第二层组成的树是一颗满二叉树,最后一层的节点要满足从左往右排列。
好,关于二叉树的概念,我们就介绍到这里,下面我们来介绍二叉树的前序、中序、后序遍历。
在此之前呢,我们先创建一颗二叉树:
class BinaryTree:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def get(self):
return self.data
def getLeft(self):
return self.left
def getRight(self):
return self.right
def setLeft(self, node):
self.left = node
def setRight(self, node):
self.right = node
好,这里我们定义好了一个二叉树类,并给它添加了一下方法,然后我们来实例化一颗二叉树:
binaryTree = BinaryTree(0)
binaryTree.setLeft(BinaryTree(1))
binaryTree.setRight(BinaryTree(2))
binaryTree.getLeft().setLeft(BinaryTree(3))
binaryTree.getLeft().setRight(BinaryTree(4))
binaryTree.getRight().setLeft(BinaryTree(5))
binaryTree.getRight().setRight(BinaryTree(6))
实例化好的二叉树是长这个样子的:
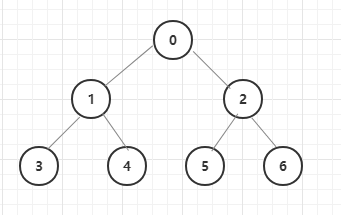
前序遍历
接下来,我们对这棵树进行前序遍历。在此之前,我们介绍一下什么是前序遍历。
前面我们介绍过了树的深度优先遍历和广度优先遍历,这里就不再赘述了。
前序遍历的顺序就是先遍历树的父节点,然后遍历树的左节点,然后遍历树的右节点,以此类推。
对于我们上面定义好的二叉树来说,它的前序遍历结果就是:0 -> 1 -> 3 -> 4 -> 2 -> 5 -> 6
对于前序、中序、后序遍历来说,采用递归的方式是非常方便的。这里我们就用递归来实现一下:
def preorderTraversal(now, result=[]):
if now == None:
return result
result.append(now.data)
preorderTraversal(now.left, result)
preorderTraversal(now.right, result)
return result
print(preorderTraversal(binaryTree))
执行结果:[0, 1, 3, 4, 2, 5, 6],是不是和我们之前手动遍历的结果一样呢。
中序遍历
中序遍历的顺序是:先遍历树的左节点,再遍历树的父节点,再遍历树的右节点。
对于我们上面创建的二叉树,它的中序遍历结果就是:3 -> 1 -> 4 -> 0 -> 5 -> 2 -> 6
在前序遍历的时候是先遍历父节点,所以result.append(now.data),就在遍历左节点和右节点的前面。
而中序遍历要先遍历左节点,所以result.append(now.data)就要在遍历左节点的后面,遍历右节点的前面。
def intermediateTraversal(now, result=[]):
if now == None:
return result
intermediateTraversal(now.left, result)
result.append(now.data)
intermediateTraversal(now.right, result)
return result
print(intermediateTraversal(binaryTree))
执行结果:[3, 1, 4, 0, 5, 2, 6]
后序遍历
后序遍历顺序是:先遍历树的左节点,再遍历树的右节点,再遍历树的父节点。
对于我们上面创建的二叉树,它的后序遍历结果是:3 -> 4 -> 1 -> 5 -> 6 -> 2 -> 0
相应的递归方程为:
def postorderTraversal(now, result=[]):
if now == None:
return
postorderTraversal(now.left, result)
postorderTraversal(now.right, result)
result.append(now.data)
return result
print(postorderTraversal(binaryTree))
执行结果:[3, 4, 1, 5, 6, 2, 0]
好,今天我们关于二叉树的三序遍历就介绍到这里了,接下来我们会接着介绍更多的二叉树类型以及应用,记得关注我的文章。关于三序遍历,你还有其他的实现方法吗,留言告诉我们把。