二叉树的友好实现

1. 引言

    前些天数据结构课讲到了二叉树。学校使用的教材是《数据结构（Java版）（第4版，叶核亚）》。总觉得书中给出的二叉树（包括之前学的线性表）的实现方式不太“优雅”（面向对象），比如线性表的链式存储和实现一节中给出的SinglyList的插入方法：public Node<T> insert(int i, T t)；比如在二叉树的链式存储和实现的插入方法：public BinaryNode<T> insert(BinaryNode<T> parent, T t, boolean leftChild)；这些实现都把Node对象暴露了出去，但好的做法肯定是把它对使用者隐藏啊。我们在使用LinkedList时，有听说过Node对象吗？我们关心的是将我们需要组织的对象何时存入集合和取出集合，至于

集合内部是如何关联这些对象的，我们才不关心。但也可以理解书的做法，毕竟重点是数据结构而不是面向对象。

    于是自己稍微改进了一下书中的二叉树的实现代码，让使用时更加简单方便。

2. 实现

① 类的设计

一共有三个类：BinaryTree，BinaryTreeNode，Cursor。

1）BinaryTree对象。它代表一棵树，是直接面向使用者的。它封装了树的一些基本信息，如树根（root），游标（cursor），结点数（size），高度（height）等信息，还提供了一些方法，如获取，移动游标、获取结点数，高度，遍历树等。

2）BinaryTreeNode对象。它代表树的一个结点，是BinaryTree的静态内部类，对外透明。它封装的是一个结点的信息，如父结点（parent），左孩子结点（left），右孩子结点（right），结点的层次（level）。

3）Cursor对象。它也是BinaryTree的静态内部类，但对外公开。它表示的是一个指向树中某个结点的“指针”。使用者通过Cursor来操作树。如通过调用它的value()方法可获取当前树的Cursor指向的结点的值；调用value(T t)可修改值；调用child(T left, T right)可为当前指向的结点添加左右孩子。

② 代码

下面给出Java实现代码：

import java.util.LinkedList;

/**
 * 二叉树
 * 
 * @author D.K
 * @date 2015年10月14日 下午9:10:00
 * @Description: TODO
 */
public class BinaryTree<T> {

    public static final int ORDER_TYPE_PREORDER = 1;
    public static final int ORDER_TYPE_INORDER = 2;
    public static final int ORDER_TYPE_POSTORDER = 3;
    public static final int ORDER_TYPE_LEVEL = 4;

    private BinaryTreeNode<T> rootNode;
    private Cursor<T> cursor;
    private int size;
    private int height;

    public BinaryTree() {
    }

    public BinaryTree(T root) {
        root(root);
        size = 1;
        height = 1;
    }

    /**
     * 获取根元素
     * 
     * @return
     */
    public T root() {
        if (isEmpty()) {
            throw new RuntimeException("该树是空树！");
        }
        return rootNode.data;
    }

    /**
     * 设置树的根元素（如果有，则替换）
     * 
     * @param root
     * @return
     */
    public Cursor<T> root(T root) {
        final BinaryTreeNode<T> newRootNode = new BinaryTreeNode<>(root, null, 1);
        if (isEmpty())
            cursor = new Cursor<>(this);
        else {
            newRootNode.left = rootNode.left;
            newRootNode.right = rootNode.right;
        }
        rootNode = newRootNode;
        cursor.node = rootNode;
        return cursor;
    }

    /**
     * 将游标指向到根元素
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2Root() {
        if (!isEmpty()) {
            cursor.node = rootNode;
            return true;
        }
        return false;
    }

    /**
     * 将游标指向到当前指向元素的父元素
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2Parent() {
        if (cursor.node.parent != null) {
            cursor.node = cursor.node.parent;
            return true;
        }
        return false;
    }

    /**
     * 将游标指向到当前指向元素的父元素的左侧相邻元素
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2ParentLeftNeighbor() {
        return move2Parent() && move2LeftNeighbor();
    }

    /**
     * 将游标指向到当前指向元素的父元素的右侧相邻元素
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2ParentRightNeighbor() {
        return move2Parent() && move2RightNeighbor();
    }

    /**
     * 将游标指向到当前指向元素的祖父元素
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2Grandparent() {
        if (cursor.node.parent != null || cursor.node.parent.parent != null) {
            cursor.node = cursor.node.parent.parent;
            return true;
        }
        return false;
    }

    /**
     * 将游标指向到当前指向元素的祖父元素的左侧相邻元素
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2GrandparentLeftNeighbor() {
        return move2Grandparent() && move2LeftNeighbor();
    }

    /**
     * 将游标指向到当前指向元素的祖父元素的右侧相邻元素
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2GrandparentRightNeighbor() {
        return move2Grandparent() && move2RightNeighbor();
    }

    /**
     * 将游标移动到当前指向元素的左孩子
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2LeftChild() {
        if (cursor.node.left != null) {
            cursor.node = cursor.node.left;
            return true;
        }
        return false;
    }

    /**
     * 将游标移动到当前指向元素相邻左侧的元素（可能是兄弟，也可能不是兄弟）
     * 
     * @return
     */
    public boolean move2LeftNeighbor() {
        if (cursor.node == rootNode) {
            return false;
        }
        if (cursor.isRightChild()) {
            // 当前指向元素是其父元素的右孩子，这种情况很简单
            if (cursor.node.parent.left != null) {
                cursor.node = cursor.node.parent.left;
                return true;
            }
            return false;
        }
        // 当前指向元素是其父元素的左孩子
        // 创建临时移动的cursor
        final Cursor<T> tempCursor = new Cursor<>(cursor);
        final int level = tempCursor.level();
        while (Cursor.isLeftChild(tempCursor.node.parent)) {
            tempCursor.node = tempCursor.node.parent;
        }
        // 此时tempCursor指向元素的父元素是根元素或右孩子
        if (tempCursor.node.parent == rootNode) {
            return false;
        }
        // tempCursor移动到当前元素的祖父元素的左孩子
        tempCursor.node = tempCursor.node.parent.parent.left;
        while (tempCursor.node.right != null && tempCursor.node.right.level != level) {
            tempCursor.node = tempCursor.node.right;
        }
        final boolean result = tempCursor.node.right != null;
        if (result) {
            cursor.node = tempCursor.node.right;
        }
        return result;
    }

    /**
     * 将游标移动到当前指向元素相邻右侧的元素（可能是兄弟，也可能不是兄弟）
     * 
     * @return
     */
    public boolean move2RightNeighbor() {
        if (cursor.node == rootNode) {
            return false;
        }
        if (cursor.isLeftChild()) {
            // 当前指向元素是其父元素的左孩子，这种情况很简单
            if (cursor.node.parent.right != null) {
                cursor.node = cursor.node.parent.right;
                return true;
            }
            return false;
        }
        // 当前指向元素是其父元素的右孩子
        // 临时移动的cursor
        final Cursor<T> tempCursor = new Cursor<>(cursor);
        final int level = tempCursor.level();
        while (Cursor.isRightChild(tempCursor.node.parent)) {
            tempCursor.node = tempCursor.node.parent;
        }
        // 此时tempCursor指向元素的父元素是根元素或右孩子
        if (tempCursor.node.parent == rootNode) {
            return false;
        }
        // tempCursor移动到当前元素的祖父元素的右孩子
        tempCursor.node = tempCursor.node.parent.parent.right;
        while (tempCursor.node.left != null && tempCursor.node.left.level != level) {
            tempCursor.node = tempCursor.node.left;
        }
        final boolean result = tempCursor.node.left != null;
        if (result) {
            cursor.node = tempCursor.node.left;
        }
        return result;
    }

    /**
     * 将游标移动到当前指向元素的右孩子
     * 
     * @return true表示移动成功；否则表示移动失败（要移自的位置没有元素）。
     */
    public boolean move2RightChild() {
        if (cursor.node.right != null) {
            cursor.node = cursor.node.right;
            return true;
        }
        return false;
    }

    public void foreach(OnForeachListener foreachListener) {
        foreach(ORDER_TYPE_PREORDER, foreachListener);
    }

    public void foreach(int orderType, OnForeachListener foreachListener) {
        switch (orderType) {
        case ORDER_TYPE_POSTORDER:
            postorder(rootNode, foreachListener);
            break;
        case ORDER_TYPE_INORDER:
            inorder(rootNode, foreachListener);
            break;
        case ORDER_TYPE_LEVEL:
            levelorder(foreachListener);
            break;
        case ORDER_TYPE_PREORDER:
        default:
            preorder(rootNode, foreachListener);
            break;
        }
    }

    /**
     * 先根遍历（递归）
     */
    private void preorder(BinaryTreeNode<T> node, OnForeachListener foreachListener) {
        if (node != null && foreachListener != null) {
            foreachListener.foreach(node.data);
            preorder(node.left, foreachListener);
            preorder(node.right, foreachListener);
        }
    }

    /**
     * 中根遍历（递归）
     */
    private void inorder(BinaryTreeNode<T> node, OnForeachListener foreachListener) {
        if (node != null && foreachListener != null) {
            inorder(node.left, foreachListener);
            foreachListener.foreach(node.data);
            inorder(node.right, foreachListener);
        }
    }

    /**
     * 后根遍历（递归）
     */
    private void postorder(BinaryTreeNode<T> node, OnForeachListener foreachListener) {
        if (node != null && foreachListener != null) {
            postorder(node.left, foreachListener);
            postorder(node.right, foreachListener);
            foreachListener.foreach(node.data);
        }
    }

    /**
     * 层次遍历（非递归）
     */
    private void levelorder(OnForeachListener foreachListener) {
        BinaryTreeNode<T> node = rootNode;
        LinkedList<BinaryTreeNode<T>> linkedList = new LinkedList<>();
        while (node != null && foreachListener != null) {
            foreachListener.foreach(node.data);
            if (node.left != null) {
                linkedList.offer(node.left);
            }
            if (node.right != null) {
                linkedList.offer(node.right);
            }
            node = linkedList.poll();
        }
    }
    

    /**

     * 返回树状图字符串（这里只是为了练习一下，真正的还是以广义表形式输出更妥） 

    */ 

    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        BinaryTreeNode<T> node = rootNode;
        LinkedList<BinaryTreeNode<T>> linkedList = new LinkedList<>();
        int lastLevel = -1;
        while (node.level <= height) {
            final int margin = (int) (Math.pow(2, height - node.level) - 1);
            final int space = 2 * margin + 1;
            if (node.level != lastLevel) {
                for (int i = 0; i < margin; i++) {
                    builder.append(" ");
                }
            } else {
                for (int i = 0; i < space; i++) {
                    builder.append(" ");
                }
            }
            builder.append(node.data == null ? " " : node.data);
            lastLevel = node.level;
            if (node.left != null) {
                linkedList.offer(node.left);
            } else {
                linkedList.offer(new BinaryTreeNode<T>(null, node.level + 1));
            }

            if (node.right != null) {
                linkedList.offer(node.right);
            } else {
                linkedList.offer(new BinaryTreeNode<T>(null, node.level + 1));
            }

            if (linkedList.peek() != null && linkedList.peek().level != lastLevel) {
                builder.append("
");
            }

            node = linkedList.poll();
        }

        return builder.toString();
    }

    /**
     * 
     * 获取树的元素总数
     * 
     * @return
     */
    public int size() {
        return size;
    }

    /**
     * 获取树的高度
     * 
     * @return
     */
    public int height() {
        return height;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 获取游标
     * 
     * @return
     */
    public Cursor<T> getCursor() {
        return cursor;
    }

    private static class BinaryTreeNode<T> {

        T data;
        BinaryTreeNode<T> parent;
        BinaryTreeNode<T> left;
        BinaryTreeNode<T> right;
        int level;

        public BinaryTreeNode(T data, int level) {
            super();
            this.data = data;
            this.level = level;
        }

        BinaryTreeNode(T data, BinaryTreeNode<T> parent, int level) {
            this.data = data;
            this.parent = parent;
            this.level = level;
        }
    }

    /**
     * 用node1 替换 node2；
     * 
     * @param node1
     * @param node2
     */
    private void repace(BinaryTreeNode<T> node1, BinaryTreeNode<T> node2) {
        // 修改node1的父亲、左、右孩子
        node1.parent = node2.parent;
        node1.left = node2.left;
        node1.right = node2.right;
        // 修改node2左、右孩子的父亲
        if (node2.left != null) {
            node2.left.parent = node1;
        }
        if (node2.right != null) {
            node2.right.parent = node1;
        }
        // 修改node2父亲的孩子
        if (Cursor.isLeftChild(node2)) {
            node2.parent.left = node1;
        }
        if (Cursor.isRightChild(node2)) {
            node2.parent.right = node1;
        }
        // 修改root
        if (node2 == rootNode) {
            rootNode = node1;
        }
    }

    // ----------------------------------------------------------------//

    /**
     * 指向某结点的游标，用于操作和访问元素。 <b>游标默认会指向最新操作的元素。
     * 
     * @author D.K
     * @date 2015年10月14日 下午9:20:47
     * @Description
     * @param <T>
     */
    public static class Cursor<T> {

        private BinaryTree<T> binaryTree;
        private BinaryTreeNode<T> node;

        public Cursor(Cursor<T> cursor) {
            this.binaryTree = cursor.binaryTree;
            this.node = cursor.node;
        }

        private Cursor(BinaryTree<T> binaryTree) {
            this.binaryTree = binaryTree;
        }

        /**
         * 获取当前指向的元素的值
         * 
         * @return
         */
        public T value() {
            return node.data;
        }

        /**
         * 设置是当前指向元素的值
         * 
         * @param t
         */
        public void value(T t) {
            node.data = t;
        }

        /**
         * 获取当前指向的元素在树中的层次
         * 
         * @return
         */
        public int level() {
            return node.level;
        }

        /**
         * 为当前指向的元素设置左孩子（如果有，则替换）
         * 
         * @param left
         */
        public Cursor<T> leftChild(T left) {
            BinaryTreeNode<T> leftNode = new BinaryTreeNode<T>(left, node.level + 1);
            if (node.left == null) {
                // 当前结点没有左孩子，直接添加
                binaryTree.size++;
                node.left = leftNode;
                leftNode.parent = node;
                binaryTree.height = leftNode.level > binaryTree.height ? leftNode.level : binaryTree.height;
            } else {
                // 当前结点有左孩子，替换
                binaryTree.repace(leftNode, node);
            }
            node = leftNode; // 移动游标
            return this;
        }

        /**
         * 为当前指向的元素设置右孩子（如果有，则替换）
         * 
         * @param right
         */
        public Cursor<T> rightChild(T right) {
            BinaryTreeNode<T> rightNode = new BinaryTreeNode<T>(right, node.level + 1);
            if (node.right == null) {
                // 当前结点没有右孩子，直接添加
                binaryTree.size++;
                node.right = rightNode;
                rightNode.parent = node;
                binaryTree.height = rightNode.level > binaryTree.height ? rightNode.level : binaryTree.height;
            } else {
                // 当前结点有左孩子，替换
                binaryTree.repace(rightNode, node);
            }
            node = rightNode; // 移动游标
            return this;
        }

        /**
         * 为当前指向的元素设置左右孩子
         * 
         * @param left
         * @param right
         * @return
         */
        public Cursor<T> child(T left, T right) {
            leftChild(left);
            binaryTree.move2Parent();
            rightChild(right);
            return this;
        }

        /**
         * 判断当前指向的元素是否为其父元素的左孩子
         * 
         * @return true：为左孩子；false：不为左孩子或当前指向元素为根元素
         */
        public boolean isLeftChild() {
            if (node.parent == null) {
                return false;
            }
            return node.parent.left == node;
        }

        private static boolean isLeftChild(BinaryTreeNode<?> node) {
            if (node.parent == null) {
                return false;
            }
            return node.parent.left == node;
        }

        /**
         * 判断当前指向的元素是否为其父元素的右孩子
         * 
         * @return true：为右孩子；false：不为右孩子或当前指向元素为根元素
         */
        public boolean isRightChild() {
            if (node == binaryTree.rootNode) {
                return false;
            }
            return node.parent.right == node;
        }

        private static boolean isRightChild(BinaryTreeNode<?> node) {
            if (node.parent == null) {
                return false;
            }
            return node.parent.right == node;
        }

    }

    public interface OnForeachListener {
        public void foreach(Object obj);
    }
}

3. 测试

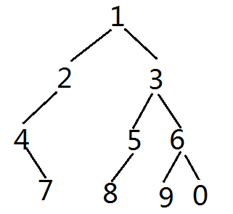
下面进行测试。比如我们要构建如下图所示的树：

我们可以很容易的做到：

public static void main(String[] args) {
    // 构建一棵树
    BinaryTree<Integer> binaryTree = new BinaryTree<>();
    // cursor在操作完成后，默认会指向最后操作的元素。
    // 如当下面root(T t)操作完成后，Cursor就指向了root。
    Cursor<Integer> cursor = binaryTree.root(1);
    // 下面操作完成后， cursor会指向3这个元素。
    cursor.child(2, 3);
    cursor.child(5, 6);
    cursor.child(9, 0);
    binaryTree.move2ParentLeftNeighbor();
    cursor.leftChild(8);
    binaryTree.move2GrandparentLeftNeighbor();
    cursor.leftChild(4);
    cursor.rightChild(7);
}

我们再通过随机访问遍某个元素、遍历这棵树和调用toString方法，来验证树是否构建地正确：

public static void main(String[] args) {
    // 构建一棵树
    BinaryTree<Integer> binaryTree = new BinaryTree<>();
    // cursor在操作完成后，默认会指向最后操作的元素。
    // 如当下面root(T t)操作完成后，Cursor就指向了root。
    Cursor<Integer> cursor = binaryTree.root(1);
    // 下面操作完成后， cursor会指向3这个元素。
    cursor.child(2, 3);
    cursor.child(5, 6);
    cursor.child(9, 0);
    binaryTree.move2ParentLeftNeighbor();
    cursor.leftChild(8);
    binaryTree.move2GrandparentLeftNeighbor();
    cursor.leftChild(4);
    cursor.rightChild(7);
    // -------------------测试------------------
    // (1) 此时cursor指向的是7这个元素，我们访问它的祖父元素的右邻居的右孩子的左孩子（应该是9）。
    if (binaryTree.move2GrandparentRightNeighbor() && binaryTree.move2RightChild() && binaryTree.move2LeftChild()) {
        System.out.println("7的祖父元素的右邻居的右孩子的左孩子是：" + cursor.value());
    } else {
        System.out.println("不存在");
    }

    // (2) 遍历树
    // 先根遍历
    System.out.print("先根遍历的结果是：");
    binaryTree.foreach(BinaryTree.ORDER_TYPE_PREORDER, new OnForeachListener() {

        @Override
        public void foreach(Object obj) {
            System.out.print(obj);
        }
    });
    // 中根遍历
    System.out.print("
中根遍历的结果是：");
    binaryTree.foreach(BinaryTree.ORDER_TYPE_INORDER, new OnForeachListener() {

        @Override
        public void foreach(Object obj) {
            System.out.print(obj);
        }
    });
    // 后根遍历
    System.out.print("
后根遍历的结果是：");
    binaryTree.foreach(BinaryTree.ORDER_TYPE_POSTORDER, new OnForeachListener() {

        @Override
        public void foreach(Object obj) {
            System.out.print(obj);
        }
    });
    System.out.println();
    // toString
    System.out.println(binaryTree);
}

结果如下图：

4. 总结

    如上给出了二叉树的构建、插入、修改、遍历的操作，初步实现到这里，还有删除、查找等操作以后再补充。

    欢迎批评和指正。