向量空间
定义
集和 - 具备某种特定性质的事物的总体,可有限,可无限, 可以理解为某种相似数据的集成 ( 如, 整数集, 实数集 )
空间 - 满足一定条件的集和
向量 - 具备大小和方向的量
向量空间 - 满足了加乘运算的集和
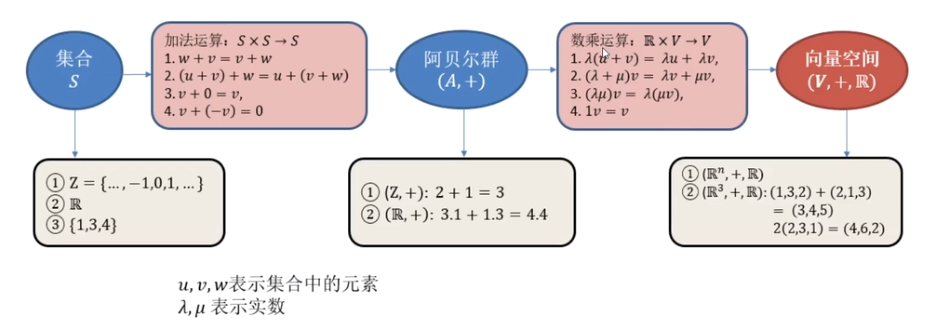
例子
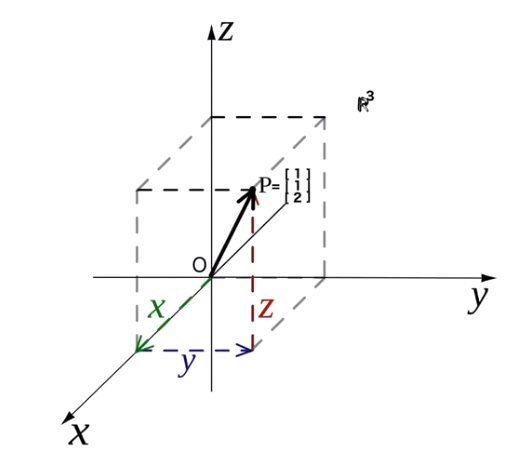
较为常见的是 n 维空间 ![]() , n 表示空间的维度, 当 n = 3 的时候, 可以理解为一个被取定了坐标系的三维空间
, n 表示空间的维度, 当 n = 3 的时候, 可以理解为一个被取定了坐标系的三维空间
空间内的每一个组都可以被一组实数列表来进行表示, 列表中的每个点为该坐标轴上的投影
向量的定义与运算
定义
向量 - 向量空间的元素为向量

运算
加法
代数角度 - 同位置相加,
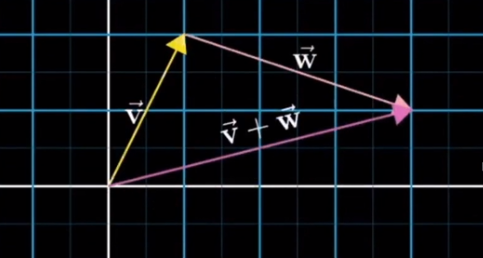
几何角度 - 按照某一个向量平移后首位相连, 计算新向量
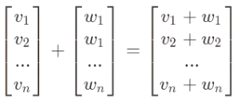
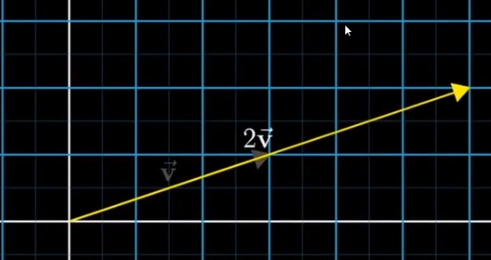
乘法
代数角度 - 变量于实数相乘, 变量中的所有数字于实数相乘即可
几何角度 - 变量在空间中的伸缩
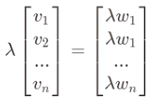
向量组的线性组合
定义
向量组 - 若干个 同维度 的列向量( 或 行向量 ) 所组成的 集和
线性组合 - ↓

意义
帮助理解 基 的概念
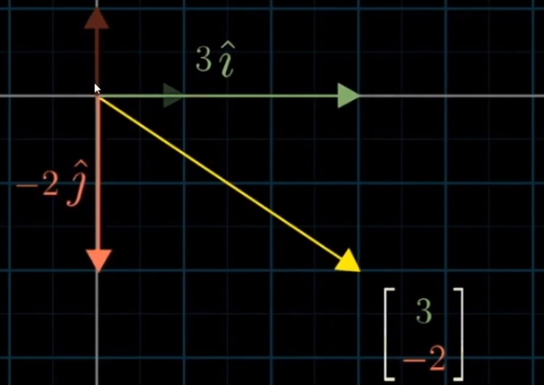
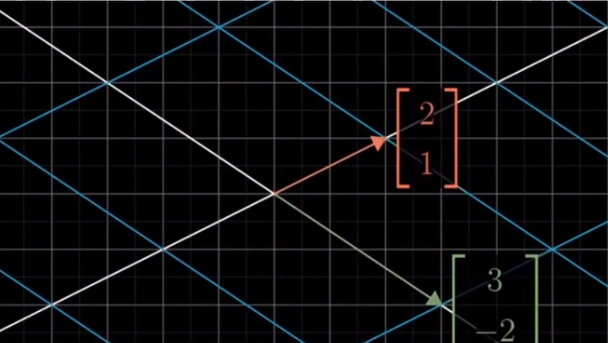
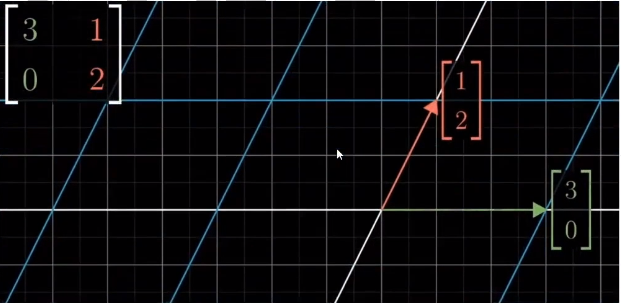
向量空间中的任何一个变量. 都可以看做是对基向量的缩放和相加操作
都可以写成两个向量的线性组合, 如图的 ![]()
帮助理解 span(张成空间) 的概念
![]()
不断的调整 ![]() 和
和 ![]() 可以得到无数的新向量, 而这些新向量的组成的集和, 就叫做张成空间
可以得到无数的新向量, 而这些新向量的组成的集和, 就叫做张成空间

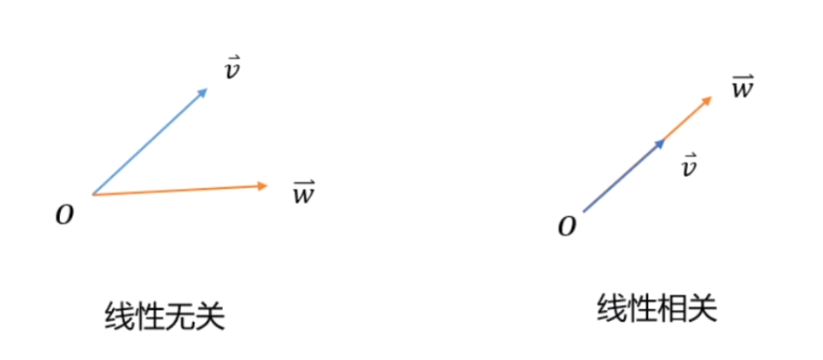
向量组的线性相关性
定义

内积和范数
定义
内积
从代数的角度来说 , 内积是两个向量之间的一种运算, 结果为一个实数

范数
范数定义了向量空间里面的距离, 最终结果依旧是个实数, 它的出现使得向量之间的比较成为了可能
一维空间中, 4, 5 两个实数的比较很容易, 但是多维度空间中的 [2,2] 和 [2,1] 如何比较?
转化为范数后即可, 范数本质上是个 函数,
常用的范数有
L1 曼哈顿距离 , 函数运算为 绝对值计算
L2 欧几里得范式, 函数的运算为 平方再开方


内积的几何解释
在了解了范数的原理之后, 就可以在几何角度上解释内积
内积定义了向量空间里的角度
u 和 v 的内积结果就是他们的 长度 * 角度
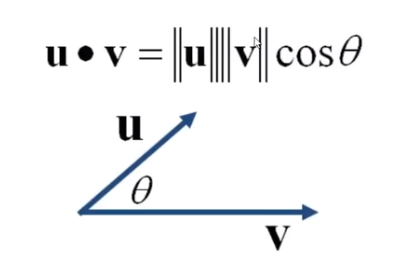
矩阵和线性变换
矩阵定义

特殊矩阵

线性变换定义
线性空间中的运动, 被称为线性变换
线性空间中的一个向量变成两一个向量, 都可以通过一个线性变换完成
向量的的线性变换必须保证原点不变 ( 基于原点旋转 ), 以及形状不变 ( 箭头不能弯曲等 )
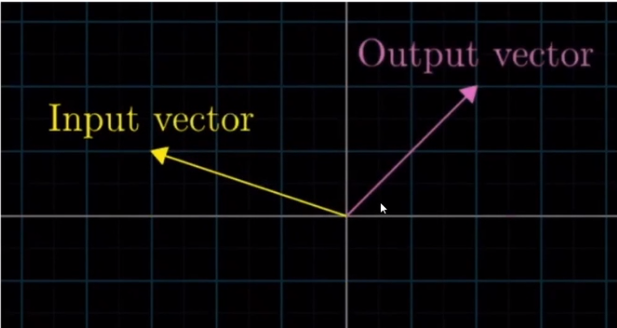
线性变换也可以对空间中的所有变量进行,比如把二维空间中的所有向量想象成充满空间的点
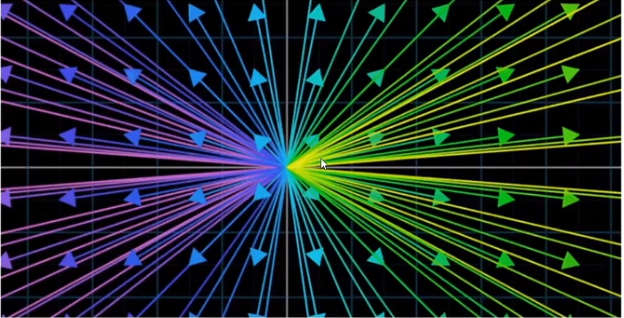
那么空间里面的线性变换, 其实相当于对空间这个平面的啦拉扯

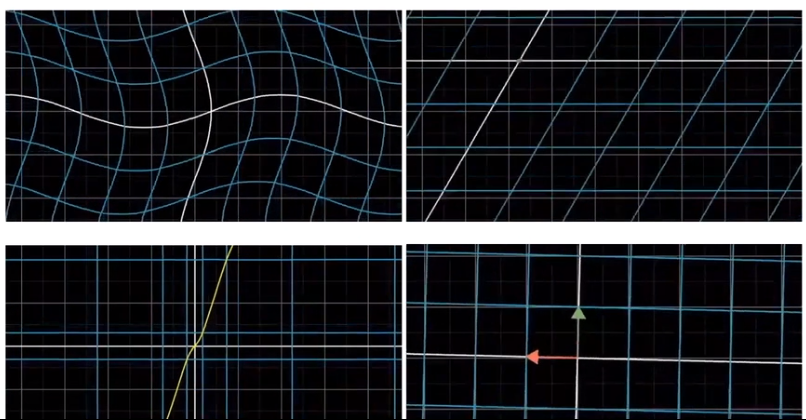
如图原始空间如下

下面4个中只有 第四个满足空间的线性变换, 1 发送了扭曲, 2 移动了原点, 3发生了扭曲
线性变换数值描述 - 矩阵
在一个线性空间中, 选定一组基向量, 将变换后的基向量的数值列表放在一个矩阵里
这个矩阵就代表了这个线性变换

原始的空间向量

拉伸后

计算结果
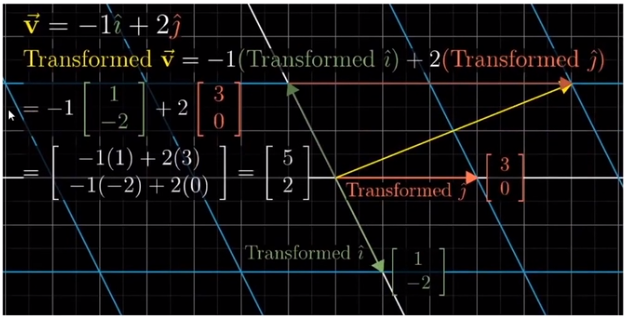
对向量施加变换的过程, 也可以用 Ax=y 来表示
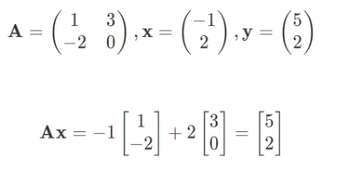
矩阵运算
加法
两个行数、列数分别相等的矩阵(同型矩阵),加法运算才有意义。
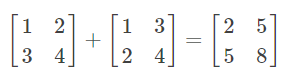
交换律:![]()
结合律:![]()
乘法
于数的乘法
数与矩阵中的每一个元素分别相乘所得的矩阵

与矩阵的乘法
设A为 ![]() 的矩阵,B为
的矩阵,B为 ![]() 的矩阵,那么称
的矩阵,那么称 ![]() 的矩阵C为矩阵A与B的乘积
的矩阵C为矩阵A与B的乘积
记作 ![]() ,其中矩阵C中的第
,其中矩阵C中的第 ![]() 行第
行第 ![]() 列元素可以表示为
列元素可以表示为
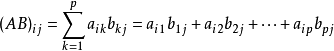
如下所示, 其实就是 A 的行向量 每个 乘上 B 的列向量
A 有两个行向量, B 有两个列向量. 最后结果为一个 4x4 的新矩阵
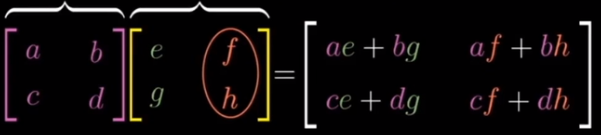
多个的也是一样的推导
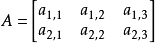
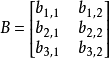
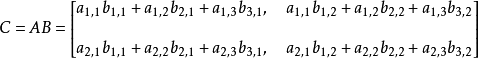
注意事项
几何意义的矩阵运算
矩阵和和向量的乘法, 本质上是向量在空间上进行线性变换
矩阵的相乘是空间上的两种线性变换的叠加
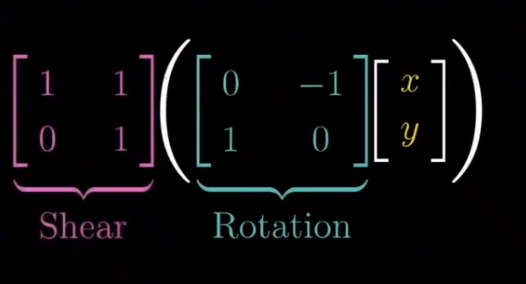
矩阵的转置

矩阵的行列式
定义
行列式是数学中的一个函数, 将一个 n * n 的矩阵 A 映射到一个纯量
记作 det(A) 或者 |A|
注意
矩阵的行列式只针对方阵 (行数和列数相等) 有效
计算
对角线上的元素相乘后减法累积
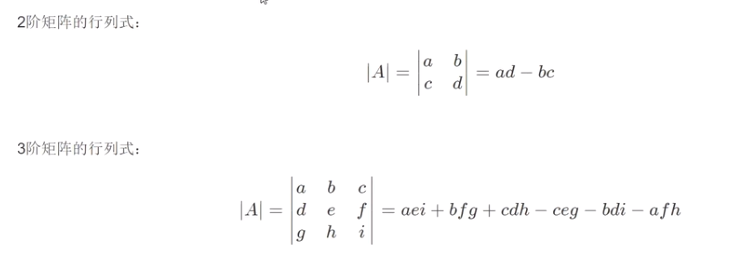
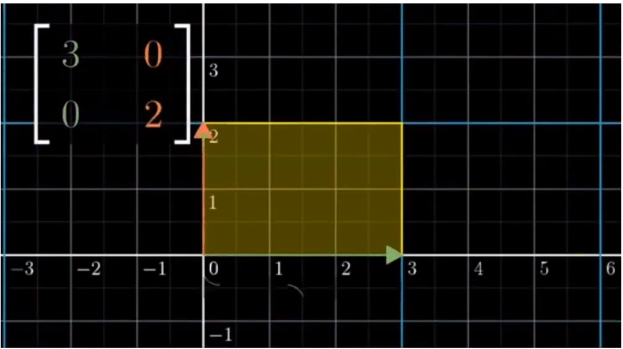
几何意义
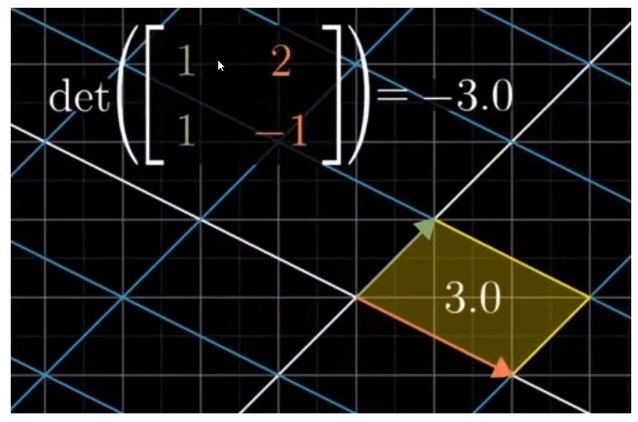
在二维空间中, 行列式表示矩阵对应的线性变化前后的面积比
在高维空间, 表示体积
如果一个矩阵的行列式为负数, 说明空间里面的向量都进行了 180°的翻转
逆矩阵
定义

例如
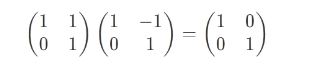
几何意义
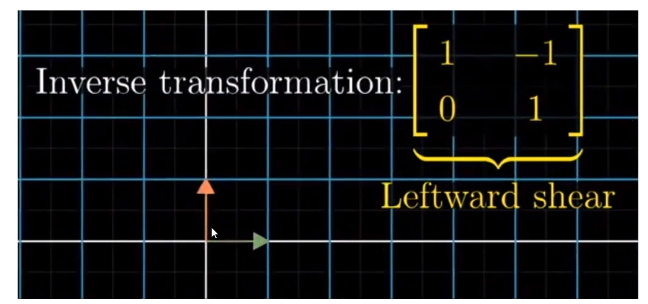
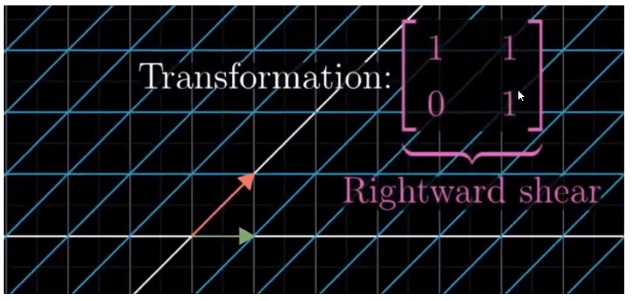
一个矩阵的逆矩阵代表是该矩阵的反运动
求解线性方程组
任何一个线性方程组都可以写成矩阵和向量相乘得到另一个向量, 比如
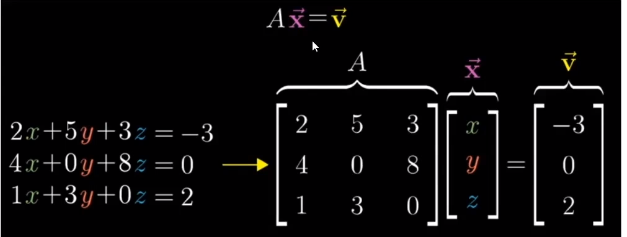
矩阵和向量的乘法相当于在一个矩阵A描述的线性变换



如果逆矩阵不存在, 那也也存在两种情况
线性变换将空间中的所有变量变成一条直线上,
那么得到的结果可能也会在这个直线上, 或者不在直线上
如果在这个直线上, 则可以计算出 x 的解
如果不在直线上, 则表示 x 变量不存在 , 则这个线性方程组不存在任何解

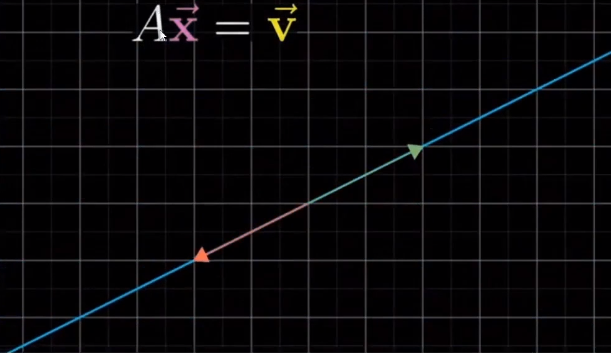

特征值和特征向量
定义

几何上理解
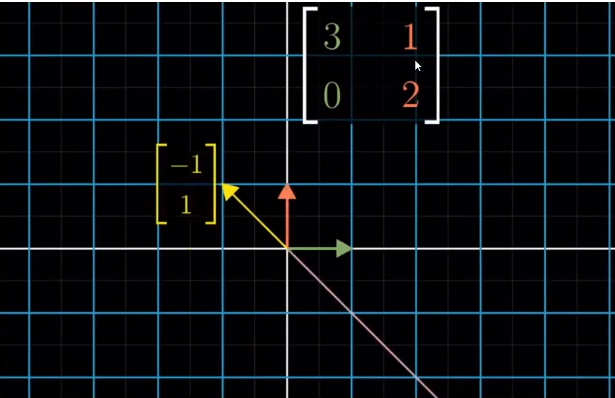
特征向量就是线性变换后还留在原来直线上的向量 ( 没有发生旋转和方向上的改变)
特征值就是特征向量的缩放系数

意义
对比普通的线性变换对坐标进行的改变,
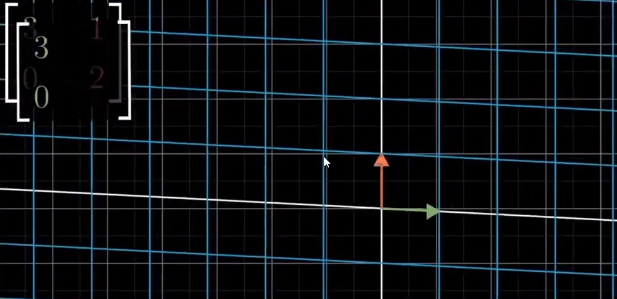
也可以通过特征值和特征向量来理解和标识
对角矩阵
对角矩阵较为特殊, 对角矩阵 --- 主对角线之外的元素皆为0的矩阵
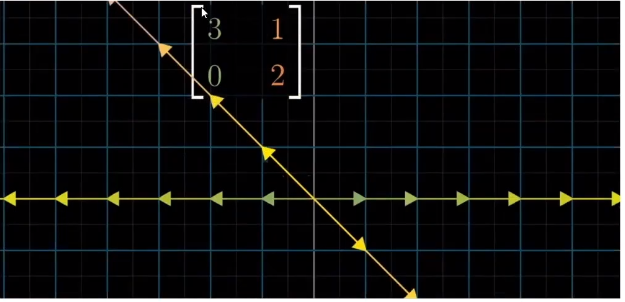
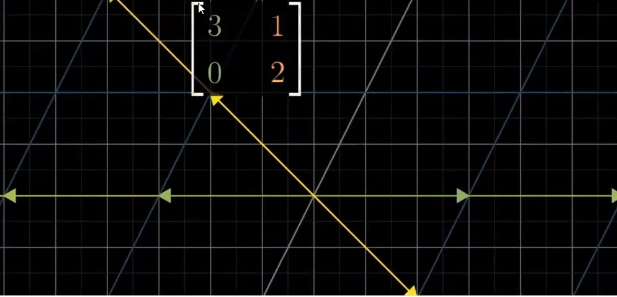
这个矩阵的每一列向量都是特征向量, 特征值就是对角线上的值
相当于在各自方向上的伸缩.
对称矩阵和正定矩阵
理解定义就好..
定义 1

定义 2

相似矩阵和对角化
理解定义就好..
相似矩阵

对角化

二次型
引例
一元二次函数

对于一元二次函数, 给他添加一次项是不会让他的形状发生改变的
仅仅是一定程度的平移而已
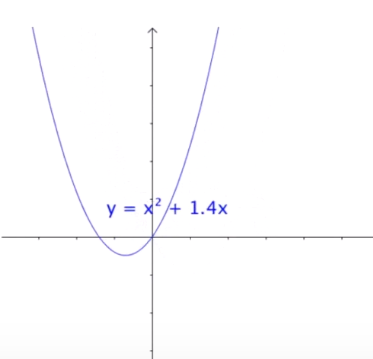
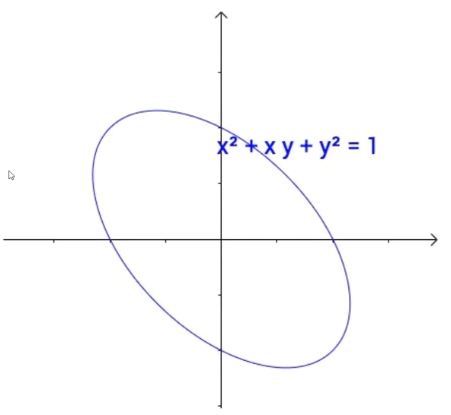
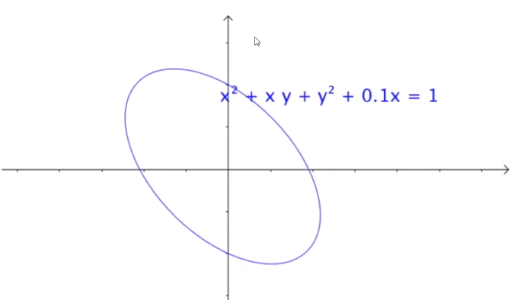
对于二元二次方程也是同理
添加一个一次项后也是平移效果
定义
人话, 某一个有n个变量, 但是每个变量的最高次数都是二次, 这样的形式就叫做 二次型

人话, 任何一个二次型, 都可以用矩阵和变量相乘的形式来表达
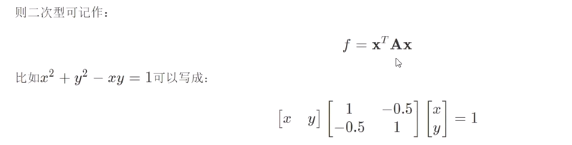
结论

总结
- 向量空间是定义类加法和数乘这两种运算的集合
- 范数定义了向量空间中的距离, 内积定义了向量空间里的角度
- 线性变换描述了向量在空间里面的变化
- 矩阵就是空间中线性变换的数值表示
- 矩阵的行列式代表矩阵对应的线性变换后的面积 (二维实数空间中, 三维表示体积)
- 逆矩阵的行列式代表矩阵对应的线性变换的反运动
- 矩阵的特征值和特征向量描述了线性变换的速度和方向
- 线代里的二次型, 就是通过一个对称矩阵, 去研究某个二次型