NOIP2018 D2T3 保卫王国

学习自： @秦淮岸

Force

如果没有限制条件，那么这道题就跟战略游戏 (or) 没有上司的舞会是一样的，只需(dp)一次就够了，所以很容易想到一个 (44pts) 的暴力：对于每次询问，都跑一遍 (dp)，其中让 (a, b) 两个点强制转移（放/放）即可。

Thoughts

无解情况

显然，一般来说都是有解的，除非：

• 命令冲突，即(a = b) ，且 (x ot= y)
• ((a, b)) 有一条边，即存在父子关系，而两个都不能放，即 (x = 0 & y = 0)

分部分

发现若用暴力，很多地方的 (dp) 显然都是相同的。

这道题核心是：相邻两个点上必须有一个点有守卫

那么我们考虑把每次询问，将整张图分成若干个好预处理的部分，每个部分分开处理，让每个部分内部符合条件，让每个部分交界处满足条件。因为每个部分互不干扰，所以可以相对取 (min) 最优解。

考虑简单的情况， ((a, b)) 在一条链上：

PS：((a, b)) 是对称的，如果(a)在底下咱们(swap)一下就行了

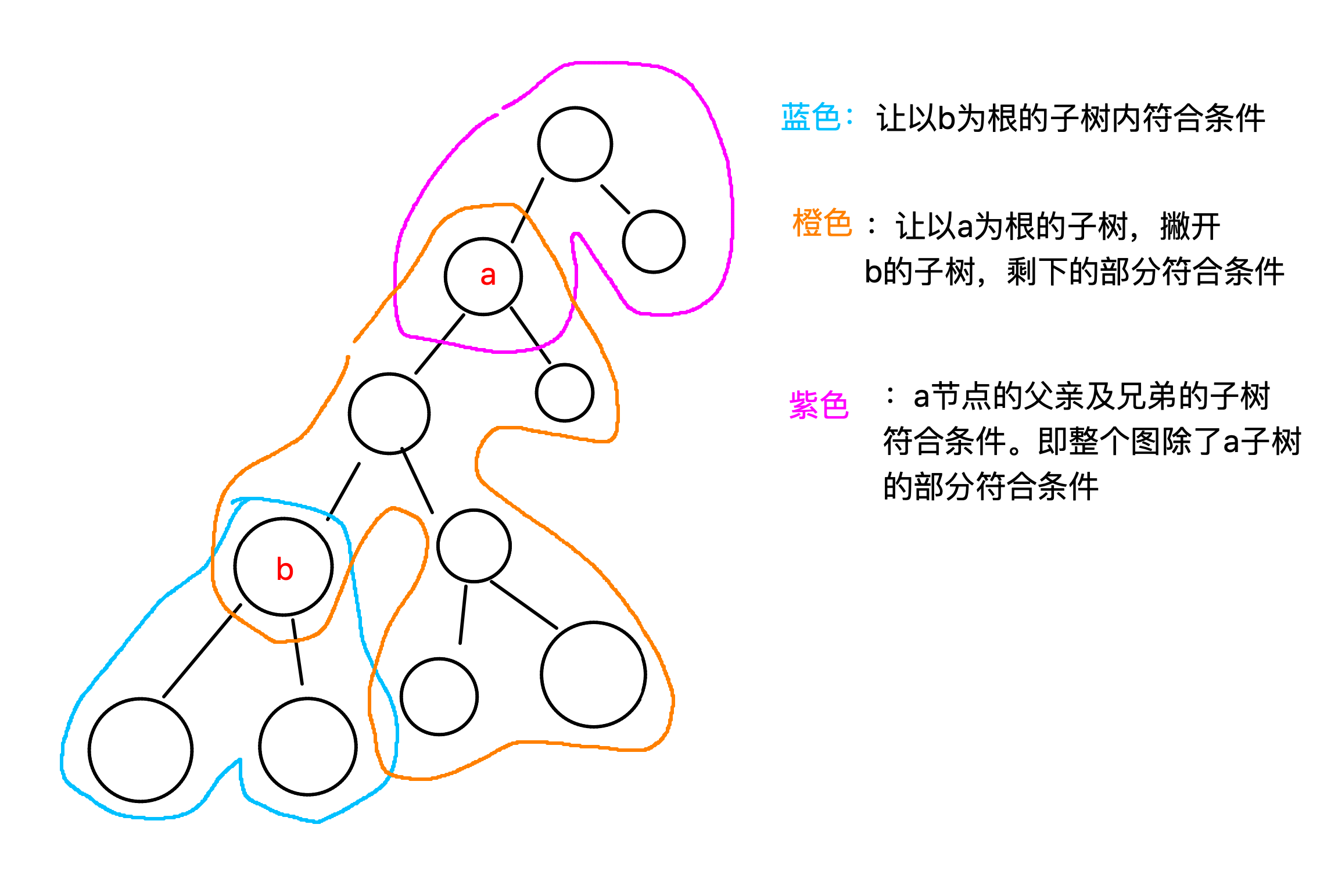
那么如果((a, b)) 不在一条链上，我们可以把它看做两条链：

1. (a) 到 (lca)
2. (lca) 到 (b)

具体情况如下图

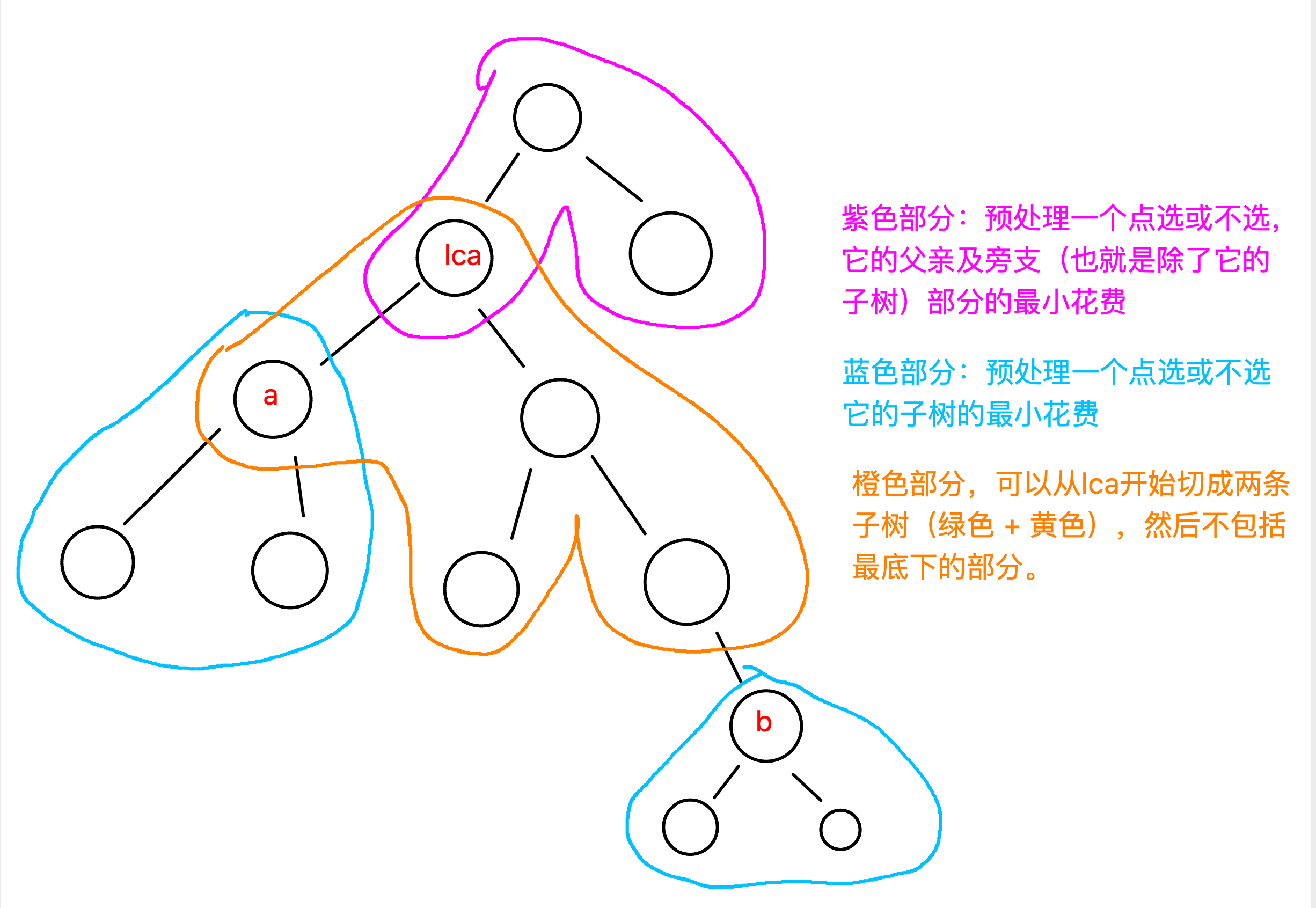
所以，一切 ((a, b)) 询问我们都可以归为以上两种情况，我们只需要用预处理大法求出来每一个部分的最小花费，求和就行了！

注意，为了不让交点重复计算，我们可以让橙色部分不算(a, b)的花费，紫色部分不算(lca)的花费

蓝色部分

(f[u][0 / 1]) 表示以 (u) 为子树， (u) 不选 / 选 下面的最大价值

转移 ：

(f[u][1] = p[u])

(f[u][0] += f[v)][1]

(f[u][1] += min(f[v][0], f[v][1]))

这跟暴力、没有上司的舞会 / 战略游戏就是一样的嘛。

紫色部分

(g[u][0 / 1]) 表示除了 (u) 的子树，剩下的 不选 / 选 下面的最大价值

转移：

(g[v][1] = p[v])

(g[v][0] = g[u][1] + f[u][1] - min(f[v][0], f[v][1]);)

$g[v][1] = min(g[v][0], g[u][0] + f[u][0] - f[v][1]); $

这个思想类似于 1073. 树的中心，从父亲向儿子 (dp)

橙色部分

因为不论怎样我们都要搞 (lca)，所以我们不妨边倍增跳，边求解。顺便维护倍增最小花费。

$w[u][0 / 1][i][0 / 1] $

设 (z = u) 往上跳 (2 ^ i) 步的点

(u) 强制不选/选；(z) 强制不选 / 选。 以 (z) 的子树中，不包含 (u) 子树的最小花费。

初始化，这里的转移由蓝色部分逆推回去，既然 (f[u][1 / 0])代表以 (u)为子树的最小花费，我再减掉相应 (v) 的贡献不就行了吗？

(w[v][0][0][0] = -inf)

(w[v][0][0][1] = f[u][1] - min(f[v][0], f[v][1]))

(w[v][1][0][0] = f[u][0] - f[v)][1]

(w[v][1][0][1] = w[v][0][0][1];)

(Q)：这边不是应该 (w[v][1][0][1] = min(w[v][0][0][1], w[v][1][0][0])) 吗，两边都可以放，所以两种情况取(min)啊？

(A)：注意这里 (dp) 的含义是强制选，所以一条边儿子爸爸都要选，因为儿子的贡献不交给他算，所以它的贡献等价于 (w[v][0][0][1])

倍增，枚举中间点选不选：

(w[u][x][i][y] = min(w[u][x][i][y], w[u][x][i - 1][z] + w[fa[u][i - 1]][z][i - 1][y]); (0 <= x, y, z <= 1))

最后(dp)求解，与倍增数组 (w) 的处理方式一样，倍增跳即可，注意，(LCA)分选 (or) 不选两种情况取 (min)。

时间复杂度

预处理 (O(Nlog_2N))，每次询问 (O(Mlog_2N))

故总复杂度 (O((N + M)log_2N))

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 100005, L = 18;

int n, m, p[N];
char type[10];
int head[N], numE = 0;
LL f[N][2], g[N][2], w[N][2][L][2];
int fa[N][L], dep[N];
struct E{
    int next, v;
}e[N << 1];
void add(int u, int v) {
    e[++numE] = (E) { head[u], v };
    head[u] = numE;
}

void dfs0(int u) {
    f[u][1] = p[u];
    for (int i = 1; i < L && fa[u][i - 1]; i++){
        fa[u][i] = fa[fa[u][i - 1]][i - 1];
    }
    for (int i = head[u]; i; i = e[i].next) {
        int v = e[i].v;
        if(v == fa[u][0]) continue;
        dep[v] = dep[u] + 1;
        fa[v][0] = u;
        dfs0(v);
        f[u][0] += f[v][1];
        f[u][1] += min(f[v][0], f[v][1]);

    }
} 
void dfs2(int u) {
    for (int i = head[u]; i; i = e[i].next) {
        int v = e[i].v;
        if(v == fa[u][0]) continue;

        w[v][0][0][1] = f[u][1] - min(f[v][0], f[v][1]);
        w[v][1][0][0] = f[u][0] - f[v][1];
        w[v][1][0][1] = w[v][0][0][1];
        dfs2(v);
    }
}
void dfs1(int u) {

    for (int i = 1; i < L && fa[fa[u][i - 1]][i - 1]; i++) {
        for (int x = 0; x <= 1; x++) {
            for (int y = 0; y <= 1; y++) {

                for (int z = 0; z <= 1; z++) {
                    w[u][x][i][y] = min(w[u][x][i][y], w[u][x][i - 1][z] + w[fa[u][i - 1]][z][i - 1][y]);
                }
            }
        }
    }

    for (int i = head[u]; i; i = e[i].next) {
        int v = e[i].v;
        if(v == fa[u][0]) continue;

        g[v][0] = g[u][1] + f[u][1] - min(f[v][0], f[v][1]);
        g[v][1] = min(g[v][0], g[u][0] + f[u][0] - f[v][1]);
        dfs1(v);
    }
}

LL inline dp(int a, int x, int b, int y) {
    LL nx[2], ny[2], tx[2], ty[2];
  	// nx, ny 表示从开始跳到当前的 a, b 点，这个点放不放军队的最小花费
    if(dep[a] < dep[b]) {
        swap(x, y); swap(a, b);
    }
  	// 先跳到同一深度
    memset(tx, 0x3f, sizeof tx);
    memset(ty, 0x3f, sizeof ty);
    tx[x] = f[a][x], ty[y] = f[b][y];
    for (int i = L - 1; ~i; i--) {
        if(dep[a] - (1 << i) < dep[b]) continue;
        memset(nx, 0x3f, sizeof nx);
        for (int u = 0; u <= 1; u++) {
          	// u：上一个选不选；v 这一个选不选
            for (int v = 0; v <= 1; v++) {
                nx[v] = min(nx[v], tx[u] + w[a][u][i][v]);
            }
        }
        memcpy(tx, nx, sizeof nx);
        a = fa[a][i];
    }
		
  	// 一条链的情况直接返回
    if(a == b) return tx[y] + g[b][y];
		
  
  	// 一起挖往上跳
    for (int i = L - 1; ~i; i--) {
        if(fa[a][i] == fa[b][i]) continue;
        memset(nx, 0x3f, sizeof nx);
        memset(ny, 0x3f, sizeof ny);
        for (int u = 0; u <= 1; u++) {
            for (int v = 0; v <= 1; v++) {
              	// u：上一个选不选；v 这一个选不选
                nx[v] = min(nx[v], tx[u] + w[a][u][i][v]);
                ny[v] = min(ny[v], ty[u] + w[b][u][i][v]);
            }
        }
        memcpy(tx, nx, sizeof nx);
        memcpy(ty, ny, sizeof ny);

        a = fa[a][i];
        b = fa[b][i];

    }
    int lca = fa[a][0];
  	// res0：不选 lca; res1：选lca
    LL res0 = g[lca][0] + f[lca][0] - f[a][1] - f[b][1] + tx[1] + ty[1];
    LL res1 = g[lca][1] + f[lca][1] - min(f[a][1], f[a][0]) - min(f[b][0], f[b][1]) + min(tx[1], tx[0]) + min(ty[1], ty[0]);
    return min(res0, res1);
}

int main(){
  	// 读入
    memset(w, 0x3f, sizeof w);
    scanf("%d%d%s", &n, &m, type);
    for (int i = 1; i <= n; i++) scanf("%d", p + i);
    for (int i = 1, u, v; i < n; i++) {
        scanf("%d%d", &u, &v);
        add(u, v); add(v, u);
    }
    dep[1] = 1;
  	// 处理 dep, fa, f 数组
    dfs0(1);
  	// 初始化 w 数组
    dfs2(1);
  	// 倍增 w 数组 + 处理 g 数组
    dfs1(1);
  
  	// 询问
    for (int i = 1, a, x, b, y; i <= m; i++) {
        scanf("%d%d%d%d", &a, &x, &b, &y);
      	// 无解判断：仅当 x -> y 存在一条边且两个都不让放，就GG了
        if(!x && !y && (fa[a][0] == b || fa[b][0] == a)) {
            puts("-1");
        } else {
            printf("%lld
", dp(a, x, b, y));
        }
    }
    return 0;
}