1,什么是线索化二叉树?
1,将二叉树转换为双向链表的过程(非线性 ==> 线性);
1,实际工程开发中,很大一部分情况下,二叉树一旦建立之后,就不会轻易改动,一般的用于遍历,并且这种操作一般执行很多;
2,先中后序遍历都是递归完成的,实际工程开发中,对一棵已经建立的二叉树反复执行先序遍历,效率低,所以不推荐反复的递归的遍历;
3,直接将遍历后的结果保存下来,下一次遍历直接用这个结果就可以;
4,工程开发中还有一种常见情况,就是要反复的知道某个结点在中序遍历下,前驱结点是谁、后继结点是谁,需要这三个结点一起来判断是否要执行后续的操作,这个时候也需要遍历、反复多次;
5,因此线性化二叉树就被创建出来,高效访问;
2,能够反映某种二叉树的遍历次序(结点的先后访问次序):
1,利用结点的 right 指针指向遍历(某种遍历)中的后继结点;
2,利用结点的 left 指针指向遍历(某种遍历)中的前驱结点;
2,如何对二叉树进行线索化?
1,思维过程:

3,二叉树的线索化:
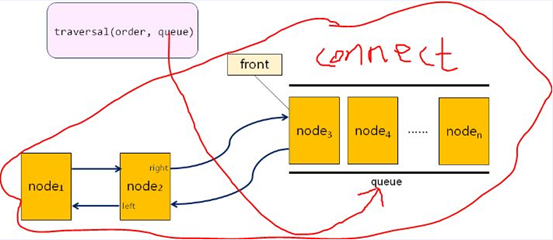
1,用traversal() 函数把树结点放到队列中,然后通过connect() 函数将right 指针指向后继,left 指针指向前驱;
4,课程目标:
1,新增(在“树——二叉树的先序、中序和后续中”已经重构并存在了)功能函数 traversal(order, queue);
1,按照某种方式对二叉树进行遍历,并将遍历时结点访问的先后次序保存在 queue 中;
2,新增遍历方式 BTTraversal::LevelOrder;
1,在 traversal(order, queue)中新增层次遍历;
3,新增共有函数 BTreeNode<T>* thread(BTTraversal order);
1,用于根据遍历次序 order 执行线索化,线索化后结果为指向双向链表首元素的指针;
4,消除遍历和线索化的代码冗余(代码重构);
5,遍历功能函数代码实现:
1 /* 遍历的功能函数,第二个参数用于保存访问时,结点的先后顺序 */ 2 void traversal(BTTraversal order, LinkQueue<BTreeNode<T>*>& queue) 3 { 4 switch(order) 5 { 6 case PreOrder: 7 PreOrderTraversal(root(), queue); 8 break; 9 case InOrder: 10 inOrderTraversal(root(), queue); 11 break; 12 case PostOrder: 13 postOrderTraversal(root(), queue); 14 break; 15 case LevelOrder: 16 levelOrderTraversal(root(), queue); 17 break; 18 default: 19 THROW_EXCEPTION(InvalidParameterException, "Parameter order is invalid ..."); 20 break; 21 } 22 }
6,层次遍历算法小结:
1,将根结点压入队列中;
2,访问队头元素指向的二叉树结点;
3,队头元素弹出,将队头元素的孩子压入队列中;
4,判断队列是否为空(非空:转 2,空:结束);
7,层次遍历算法示例:
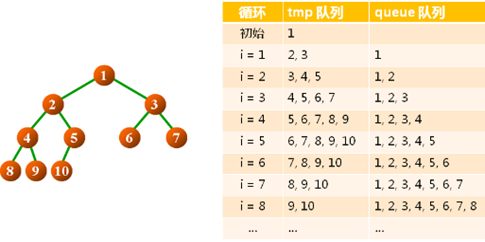
8,层次遍历算法流程:
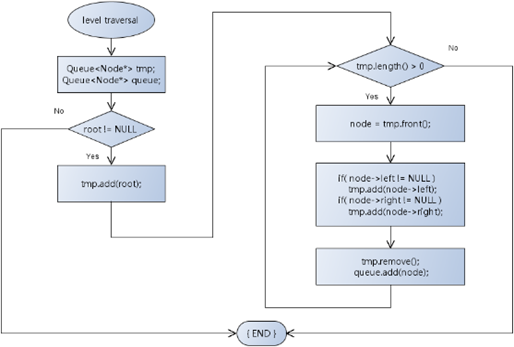
9,实现见代码;
1 /* 实现层次遍历算法 */ 2 void levelOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue) 3 { 4 if( node != NULL ) // 树不为空 5 { 6 LinkQueue<BTreeNode<T>*> tmp; // 创造辅助队列 7 tmp.add(node); // 先将根结点压入队列 8 9 while( tmp.length() > 0 ) 10 { 11 BTreeNode<T>* n = tmp.front(); // 拿到 tmp 头部结点 12 13 if( n->left != NULL ) 14 { 15 tmp.add(n->left); 16 } 17 18 if( n->right != NULL ) 19 { 20 tmp.add(n->right); 21 } 22 23 tmp.remove(); // 移动 tmp 头部的结点 24 25 queue.add(n); // 保存遍历结果 26 } 27 } 28 }
10,函数接口设计:
1,BTreeNode<T>* thread(BTTraversal order)
1,根据参数 order 选择线索化的次序(先序,中序,后序,层次);
2,返回值线索化之后指向链表首结点的指针;
1,既然要不停地访问,为何不用顺序表而要用链表?
3,线索化执行结束后对应的二叉树变为空树;
1,二叉树中的结点已经被从排列为一个线性链表了,二叉树也就不存在了,所以要变为空树;
11,线索化流程:
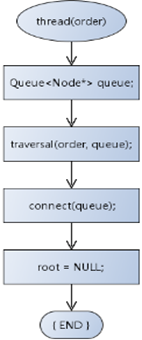
12,队列中结点的连接算法(connect(queue)):

13,连接算法的代码实现:
1 /* 将 queue 队列中结点连接成双向链表,并返回双向链表首地址 */ 2 BTreeNode<T>* connect(LinkQueue<BTreeNode<T>*>& queue) 3 { 4 BTreeNode<T>* ret = NULL; 5 if( queue.length() > 0 ) // 对列不为空 6 { 7 ret = queue.front(); // 返回头结点 8 BTreeNode<T>* slider = queue.front(); // 辅助指针指向对列头结点 9 queue.remove(); // 被指向后头结点出队列 10 slider->left = NULL; // 链表头结点指向空 11 while( queue.length() > 0 ) // 链接所有结点,就像树一样、将指针重新指定好后,就能够完成相应的容器设计了; 12 { 13 slider->right = queue.front(); 14 queue.front()->left = slider; 15 slider = queue.front(); // 移动 slider 指针,指向头结点;要不然就最后只有首尾两个结点了,这点很重要; 16 queue.remove(); // 被指向后头结点出队列 17 } 18 slider->right = NULL; // 双向链表最后一个结点指向空,不然这个双向链表就是有问题的; 19 } 20 return ret; 21 }
14,二叉树的线索化:
1 /* 线索化,二叉树变为线性链表 */ 2 BTreeNode<T>* thread(BTTraversal order) 3 { 4 BTreeNode<T>* ret = NULL; // 定义返回值 5 LinkQueue<BTreeNode<T>*> queue; // 先定义对列 6 traversal(order, queue); // 遍历,后将结果放在 queue 对列中 7 ret = connect(queue); // 将对列中的结点链接,并返回链表首结点 8 this->m_root = NULL; // 结点变为链表了,树不存在了,直接置为空树;每一个成员函数后,都要考虑成员变量的属性值,这很重要! 9 m_queue.clear(); // 上面的树发生了变化,则清空树,否则组合函数执行的有问题 10 return ret; 11 }
15,小结:
1,线索化是将二叉树转换为双向链表的过程;
2,线索化之后结点间的先后次序符合某种遍历次序;
3,线索化操作将破坏原二叉树结点间的父子关系;
1,重新组织结点,使结点间的非线性关系变为线性关系;
4,线索化之后二叉树将不在管理结点的生命期;
1,二叉树已经不存在了,成为空树了;
2,对线索化之后的双向链表进行生命期管理,比如不需要的时候对双向链表进行释放,每个结点都释放,摧毁它;