树
树属于非线性结构。逻辑上的树指的是:一堆数据中包含一个称之为根的节点,其他的节点又组成了若干棵树,成为根节点的后继。


如上图所示,根节点与子树只是相对概念,在任何一棵树中都有一个根节点,而这棵树本身又可以是别的树的子树。
树的基本概念

双亲(parent)和孩子(children):一个节点的后继节点被称为该节点的孩子,相应地该节点被称为这些孩子的双亲,比如上图中的A是B,C,D的双亲。
兄弟(sibling):拥有共同双亲的节点互为兄弟节点,比如上图中B,C,D和F,G。
节点的度(degree):一个节点的孩子个数,称为该节点的度,比如A的度为3,B的度为0,C的度为1,D的度为2。
节点的层次(level):人为规定树的根节点的层次为 1,他的后代节点的层次依次加 1,比如A的层次为1,B,C,D的层次为2,E,F,G的层次为3,以此类推。
树的高度(height):树中节点层次的最大值,如上图中树的高度为4。
终端节点(terminal):度为 0 的节点,比如B,E,H,G都是叶子。
二叉树
在各种不同种类的树种,二叉树是最重要的,下列为各种不同的二叉树。
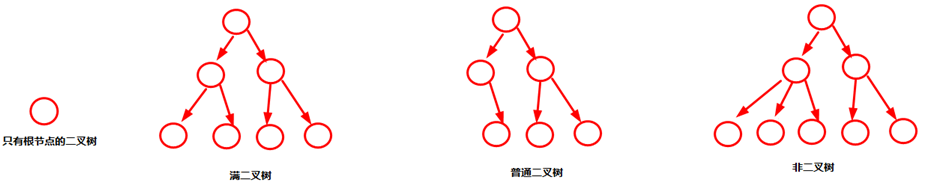
二叉搜索树
二叉搜索树除了是任意节点的度小于等于2的树外,还必须是严格区分左右节点次序的,这样就能够操作到想要操作的某个节点。
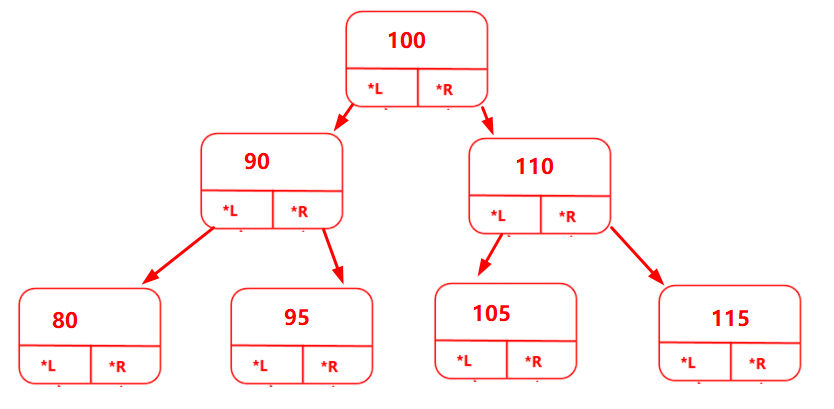
如上图所示,将大于双亲节点的值往右边存放(右孩),小于双亲节点的值往左存放(左孩)。
实验程序
节点设计
&emsp使用一个结构体来构造一个二叉搜索树。
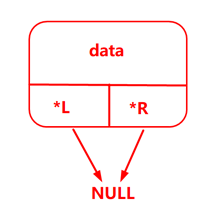
p_tree new_node(p_tree new, int data)
{
new = calloc(1, sizeof(my_tree));
if ( NULL== new)
{
perror("Memory allocation failure
");
}
new->data = data;
new->L = new->R = NULL;
return new;
}
初始化根节点
// 让用户输入新节点的数据
int input_msg(char * msg)
{
int num ;
printf("%s:
" , msg);
scanf("%d" , &num);
while(getchar() != '
');
return num;
}
p_tree init_root(p_tree new_root)
{
new_root = calloc(1, sizeof(my_tree));
if ( NULL== new_root)
{
perror("root node Memory allocation failure
");
}
new_root->data = input_msg("Please enter the root node data");
new_root->L = new_root->R = NULL;
return new_root;
}
插入节点
使用递归的方法,找到树中合适的位置将新节点插入进去。
p_tree insert_node(p_tree root, p_tree new)
{
if (NULL == root)
return new;
if (new->data < root->data)
{
root->L = insert_node(root->L, new);
}
else
{
root->R = insert_node(root->R, new);
}
}

如上图所,如果在该树中添加一个数据70,函数insert_node的调用过程如棕色箭头所示,返回过程如蓝色箭头所示。
中序遍历(从小到大)
使用中序遍历的方法来打印树中的数据。
p_tree traverse_tree(p_tree root)
{
if (NULL == root)
{
return NULL;
}
traverse_tree(root->L);
printf("%d ", root->data);
traverse_tree(root->R);
}
删除节点
将树中的指定数据删除
p_tree del_node(p_tree root, int del_data)
{
if (NULL == root)
{
return root;
}
// 如果需要删除的数据比根节点的数据小往左边找,否则右边找
if (del_data < root->data)
{
root->L = del_node(root->L, del_data);
}
else if (del_data > root->data)
{
root->R = del_node(root->R, del_data);
}
else if (del_data == root->data) //当找到需要删除的数据时,执行这个代码块
{
p_tree tmp;
if (root->L != NULL)// 如果有左孩子, 那就在左孩子中找一个最大的来替换
{
for (tmp = root->L; tmp->R != NULL; tmp=tmp->R); // 通过循环找到root2左边最右的节点 (右脚为空)
root->data = tmp->data; //替换
root->L = del_node(root->L, tmp->data); //再次递归,来删除原数据
}
else if (root->R != NULL) 如果没有左孩子, 那就在右孩子中找一个最小的来替换
{
for (tmp = root->R; tmp->L != NULL; tmp=tmp->L); // 如果没有左孩子, 那就在右孩子中找一个最小的来替换
root->data = tmp->data;
root->R = del_node(root->R, tmp->data);
}
else
{
free(root);
printf("Data deletion successful
");
return NULL;
}
}
perror("The data could not be found
");
return root;
}
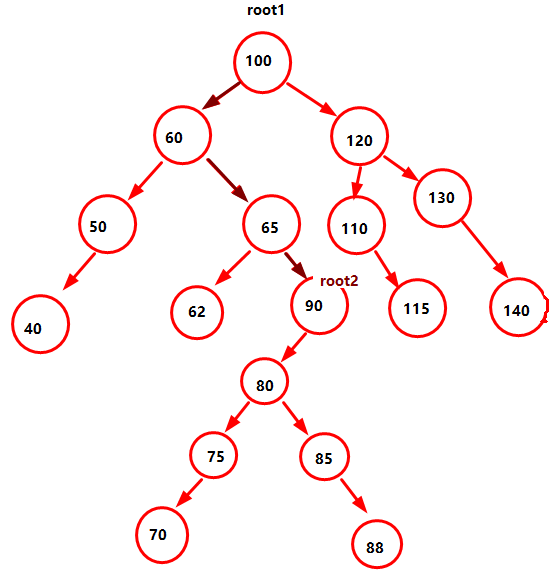
假设需要删除数据90,过程如图所示,首先经过递归找到需要删除的数据。当找到这个数据时,就以这个节点作为根节点,来查找合适替换掉这个根节点的值。经过推理,当这个根节点的左孩子存在时,就在该左孩子的右孩子中查找最大值;当左孩子不存在时,就在该右孩子的左孩子中查找最小值。最后将查找出的值替换掉需要被删除的节点。
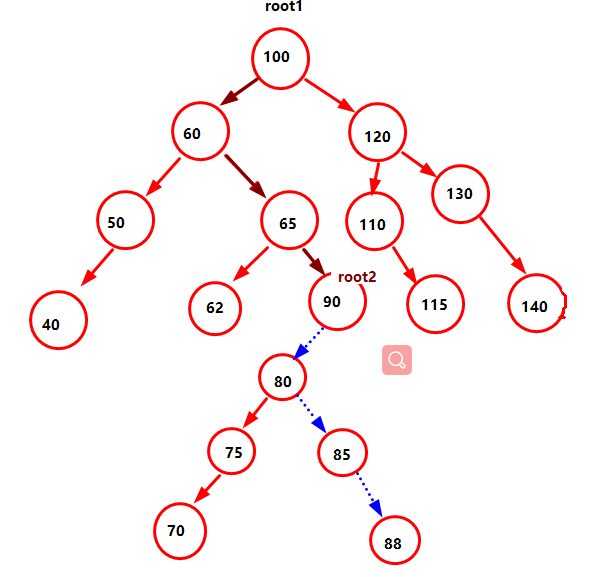
如图所示,经过for循环找到88是个合适替换掉90的值。

如图所示,当将数值88替换掉90后,就需要将原来的数据88删除,以root2的左孩子为根节点再次递归调用自己,经过递归当到达需要删除的88,将该节点指向NULL

如图所示,这是整个递归调用过程。
测试函数
int main(int argc, char const *argv[])
{
p_tree root;
int data[] = {60, 50 ,40, 65, 62, 90, 80, 75, 70, 85, 88, 120, 110, 115, 130, 140};
root = init_root(root);
p_tree new;
for (int i = 0; i < sizeof(data)/sizeof(int); i++)
{
new = new_node(new, data[i]);
insert_node(root, new);
}
traverse_tree(root);
printf("
");
int del_data = input_msg("Please enter the data you want to delete");
del_node(root, del_data);
traverse_tree(root);
printf("
");
return 0;
}