VGG 主要有两种结构,分别是 VGG16 和 VGG19,两者并没有本质上的区别,只是网络深度不一样。
对于给定的感受野,采用堆积的小卷积核是优于采用大的卷积核的,因为多层非线性层可以增加网络深度来保证学习更复杂的模式,而且代价还比较小(参数更少)。
比如,三个步长为 $1$ 的 $3 imes 3$ 卷积核的叠加,即对应 $7 imes 7$ 的感受野(即三个 $3 imes 3$ 连续卷积相当于一个 $7 imes 7$ 卷积),如果我们假设卷积输入输出的 channel 数均为 $C$,那么三个 $3 imes 3$ 连续卷积的参数总量为 $3 imes (9 C^2)$(一个卷积核的大小 $3 imes 3 imes C$,一层有 $C$ 个卷积核,总共有三层),而如果直接使用 $7 imes 7$ 卷积核,其参数总量为 $49 C^2$。很明显 $27C^2 < 49C^2$,即减少了参数。
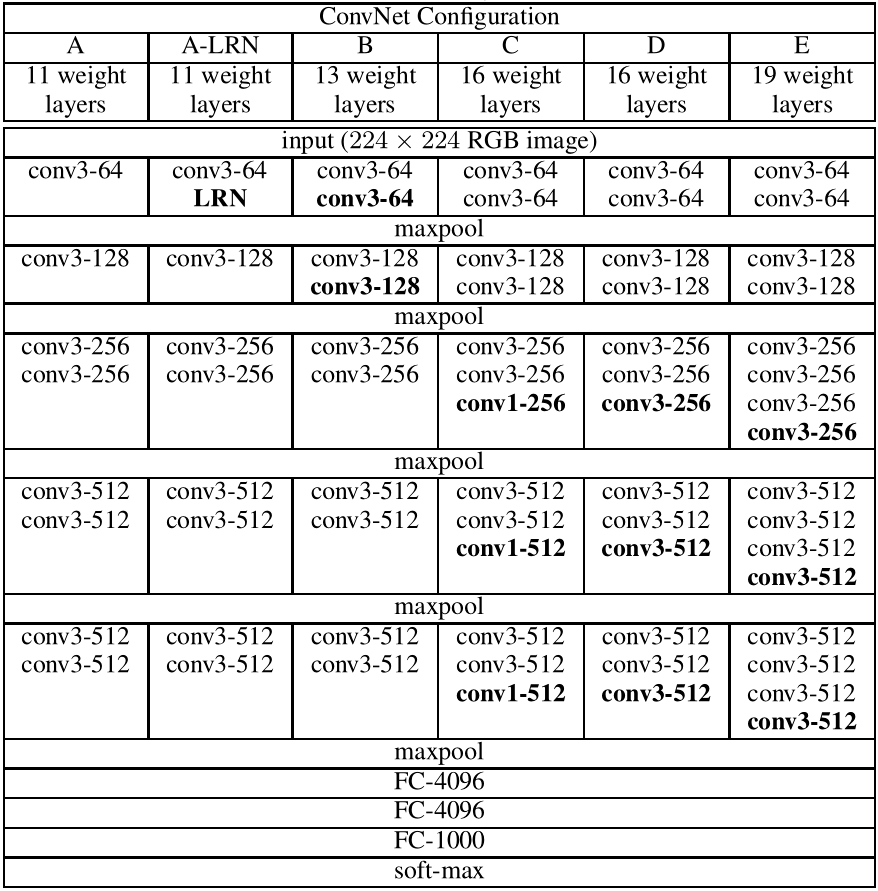
VGG的网络结构非常简单,全部都是 $(3,3)$ 的卷积核,步长为 $1$,四周补 $1$ 圈 $0$(使得输入输出的 $(H,W)$ 不变):
我们可以参考 torchvision.models 中的源码:

class VGG(nn.Module): def __init__(self, features, num_classes=1000, init_weights=True): super(VGG, self).__init__() self.features = features self.avgpool = nn.AdaptiveAvgPool2d((7, 7)) self.classifier = nn.Sequential( nn.Linear(512 * 7 * 7, 4096), nn.ReLU(True), nn.Dropout(), nn.Linear(4096, 4096), nn.ReLU(True), nn.Dropout(), nn.Linear(4096, num_classes), ) if init_weights: self._initialize_weights() def forward(self, x): x = self.features(x) x = self.avgpool(x) x = torch.flatten(x, 1) x = self.classifier(x) return x def _initialize_weights(self): for m in self.modules(): if isinstance(m, nn.Conv2d): nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu') if m.bias is not None: nn.init.constant_(m.bias, 0) elif isinstance(m, nn.BatchNorm2d): nn.init.constant_(m.weight, 1) nn.init.constant_(m.bias, 0) elif isinstance(m, nn.Linear): nn.init.normal_(m.weight, 0, 0.01) nn.init.constant_(m.bias, 0) def make_layers(cfg, batch_norm=False): layers = [] in_channels = 3 for v in cfg: if v == 'M': layers += [nn.MaxPool2d(kernel_size=2, stride=2)] else: conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1) if batch_norm: layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)] else: layers += [conv2d, nn.ReLU(inplace=True)] in_channels = v return nn.Sequential(*layers) cfgs = { 'A': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'], 'B': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'], 'D': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'], 'E': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'], } def _vgg(arch, cfg, batch_norm, pretrained, progress, **kwargs): if pretrained: kwargs['init_weights'] = False model = VGG(make_layers(cfgs[cfg], batch_norm=batch_norm), **kwargs) if pretrained: state_dict = load_state_dict_from_url(model_urls[arch], progress=progress) model.load_state_dict(state_dict) return model
cfgs 中的 "A,B,D,E" 就分别对应上表中的 A,B,D,E 四种网络结构。
'M' 代表最大池化层, nn.MaxPool2d(kernel_size=2, stride=2)
从代码中可以看出,经过 self.features 的一大堆卷积层之后,先是经过一个 nn.AdaptiveAvgPool2d((7, 7)) 的自适应平均池化层(自动选择参数使得输出的 tensor 满足 $(H = 7,W = 7)$),再通过一个 torch.flatten(x, 1) 推平成一个 $(batch\_size, n)$ 的 tensor,再连接后面的全连接层。
torchvision.models.vgg19_bn(pretrained=False, progress=True, **kwargs)
pretrained: 如果设置为 True,则返回在 ImageNet 预训练过的模型。
