博士期间估计这可能是唯一一个要编程的作业,搞了半天弄出这个东西,放这里为以后用到的时候查找方便。
说来也是可笑,读博士期间发现大家对上课也都没什么兴趣,老师也是那么回事,都说博士期间学的课程是要有助于以后科研工作用的,但是为什么大家都是呵呵的态度,对于期末的编程作业大家连题目都难以做到记得无误,也是真心无奈。
(1) 给出判断一个图是无爪图正则(每个点的度数相同)4-连通的算法,并给出时间复杂性。
该问题其实应该是这样问的,给定一个4连通正则图,如何判断其是否为无爪图,并且该图是无K4图。
由于上课真心没听懂啥,课后自己查了一些资料,最后给出以下编程代码。
首先对代码分开给出,先给出 4正则图的生成代码,作为测试数据集的生成代码。
""" 测试数据集,matrix矩阵的生成, matrix矩阵为4正则图 """ def regularFour(N=10000): matrix={} #matrix 初始化, value为集合 for k in xrange(N): matrix[k]=set() #未满足的Node列表 unfillSet=range(N) #赋值过程的终止条件,未满足Node数大于4 while(len(unfillSet)>4): k=unfillSet.pop(0) while(len(matrix[k])<4): #随机选取与其配对的点 xTemp=random.choice(unfillSet) #如果选取的点不满足条件则重选 if(xTemp in matrix[k]): continue matrix[k].add(xTemp) matrix[xTemp].add(k) if(len(matrix[xTemp])==4): unfillSet.remove(xTemp) """ 未满足点个数小于等于4, 即0,1,2,3,4 """ #未满足点为0,1,2,3,4时 while(True): #无法生成K4图,失败,返回0 if(len(unfillSet)==1): #for i in unfillSet: # print i, matrix[i] return 0, matrix #生成K4图,成功,返回1 if(len(unfillSet)==0): return 1, matrix k=unfillSet.pop(0) for xTemp in copy.copy(unfillSet): if xTemp in matrix[k]: continue else: matrix[k].add(xTemp) matrix[xTemp].add(k) if(len(matrix[xTemp])==4): unfillSet.remove(xTemp) if(len(matrix[k])==4): break #失败 if(len(matrix[k])!=4): #for i in unfillSet: # print i, matrix[i] return 0, matrix return matrix
测试结果:
判断 测试图是否 为无爪 ,非K4图。
def check(matrix): #node4Set 用于判断 K4 node4Set=set() for k in matrix: for node3 in itertools.combinations(matrix[k], 3): #判断是否有爪 a,b,c=node3 if( (a not in matrix[b]) and (a not in matrix[c]) and (b not in matrix[c]) ): print "有爪" return 0 #判断是否为K4 node4=tuple(sorted( list(node3)+[k] )) #判断4个顶点是否已经判断过 if(node4 in node4Set): continue node4Set.add(node4) flag4=0 for i in xrange(3): for j in xrange(i+1, 4): if(node4[i] in matrix[node4[j]]): flag4+=1 if(flag4==6): print "存在K4" return 0 return 1
完全的代码:
# -*- coding: utf-8 -*- import random import copy import pickle import itertools """ 测试数据集,matrix矩阵的生成, matrix矩阵为4正则图 """ def regularFour(N=10000): matrix={} #matrix 初始化, value为集合 for k in xrange(N): matrix[k]=set() #未满足的Node列表 unfillSet=range(N) #赋值过程的终止条件,未满足Node数大于4 while(len(unfillSet)>4): k=unfillSet.pop(0) while(len(matrix[k])<4): #随机选取与其配对的点 xTemp=random.choice(unfillSet) #如果选取的点不满足条件则重选 if(xTemp in matrix[k]): continue matrix[k].add(xTemp) matrix[xTemp].add(k) if(len(matrix[xTemp])==4): unfillSet.remove(xTemp) """ 未满足点个数小于等于4, 即0,1,2,3,4 """ #未满足点为0,1,2,3,4时 while(True): #无法生成K4图,失败,返回0 if(len(unfillSet)==1): #for i in unfillSet: # print i, matrix[i] return 0, matrix #生成K4图,成功,返回1 if(len(unfillSet)==0): return 1, matrix k=unfillSet.pop(0) for xTemp in copy.copy(unfillSet): if xTemp in matrix[k]: continue else: matrix[k].add(xTemp) matrix[xTemp].add(k) if(len(matrix[xTemp])==4): unfillSet.remove(xTemp) if(len(matrix[k])==4): break #失败 if(len(matrix[k])!=4): #for i in unfillSet: # print i, matrix[i] return 0, matrix return matrix def check(matrix): #node4Set 用于判断 K4 node4Set=set() for k in matrix: for node3 in itertools.combinations(matrix[k], 3): #判断是否有爪 a,b,c=node3 if( (a not in matrix[b]) and (a not in matrix[c]) and (b not in matrix[c]) ): print "有爪" return 0 #判断是否为K4 node4=tuple(sorted( list(node3)+[k] )) #判断4个顶点是否已经判断过 if(node4 in node4Set): continue node4Set.add(node4) flag4=0 for i in xrange(3): for j in xrange(i+1, 4): if(node4[i] in matrix[node4[j]]): flag4+=1 if(flag4==6): print "存在K4" return 0 return 1 if __name__=="__main__": """ 4正则数据生成 """ matrixList=[] try: f=open("back.dat", "rb") try: while(True): matrixList.append(pickle.load(f)) except EOFError: pass f.close() except IOError: f=open("back.dat", "wb") num=0 #图数目设置默认为 100 while(num<100): ans, matrix=regularFour() if ans==1: num+=1 #持久化 pickle.dump(matrix, f) matrixList.append(matrix) f.close() ###正式进行判断 for i in xrange(100): print i, check(matrixList[i])
运行结果图:
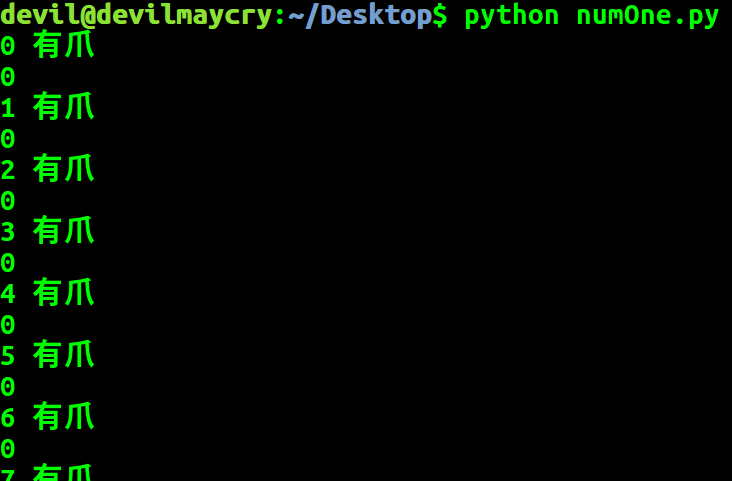
个人感觉这个东西,这么说吧,随机生成的4连通4正则图 基本都是不满足这个条件的。